双端队列广搜
1. 算法分析
双端队列广搜算法只适用于边权只有0和1的情况,本质上是对dijkstra堆优化版本的再次优化。由于dijkstra堆优化版本每次要把最小值从队头拿出,然后更新其他值后插入队列。而当边权只有0和1时,当处理的边权为0,那么更新完仍然为最小值,直接放入队头;为1则插入队尾。
2. 例题
acwing175电路维修
有一个R*C的电路板,电路板的如下:
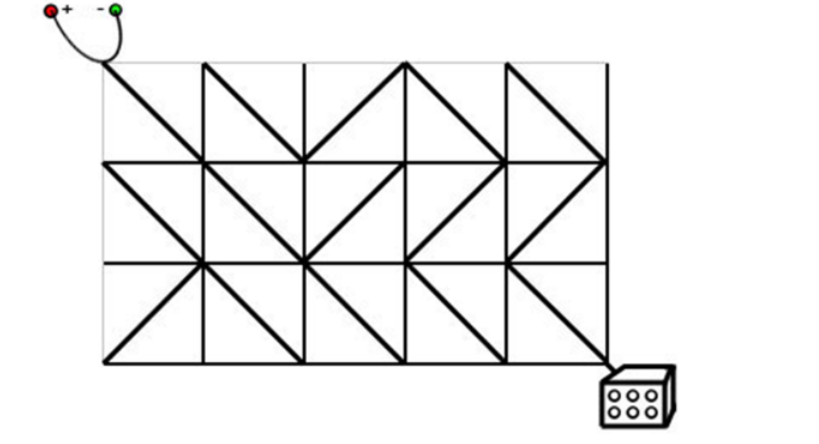
初始在左上角,现在要走到右下角。只有当线路连通才能走,问最少要改变几个电路节点,才能走到右下角。如果到不了,输出"NO SOLUTION",否则输出最小改变次数。
// 构造双端队列,每次更新最短路后
// 如果当前边为0,那么插入队头,否则插入队尾
#include <cstring>
#include <iostream>
#include <algorithm>
#include <deque>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 510, M = N * N;
int n, m;
char g[N][N];
int dist[N][N];
bool st[N][N];
int bfs()
{
memset(dist, 0x3f, sizeof dist);
memset(st, 0, sizeof st);
dist[0][0] = 0;
deque<PII> q;
q.push_back({0, 0});
char cs[] = "\/\/"; // 4个变化
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1}; // 当前点能够走到的点
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1}; // 当前点能够走到的边
while (q.size())
{
PII t = q.front();
q.pop_front();
if (st[t.x][t.y]) continue;
st[t.x][t.y] = true;
for (int i = 0; i < 4; i ++ ) // 4个方向:左上,左下,右上,右下
{
int a = t.x + dx[i], b = t.y + dy[i]; // 下一个点位置
if (a < 0 || a > n || b < 0 || b > m) continue;
int ca = t.x + ix[i], cb = t.y + iy[i]; // 下一条边位置
int d = dist[t.x][t.y] + (g[ca][cb] != cs[i]); // 距离更新
if (d < dist[a][b]) // 如果能够更新
{
dist[a][b] = d;
if (g[ca][cb] != cs[i]) q.push_back({a, b}); // 0入队头
else q.push_front({a, b}); // 1入队尾
}
}
}
return dist[n][m];
}
int main()
{
int T;
scanf("%d", &T);
while (T -- )
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);
int t = bfs();
if (t == 0x3f3f3f3f) puts("NO SOLUTION");
else printf("%d
", bfs());
}
return 0;
}