2017多校第8场 HDU 6134 Battlestation Operational 莫比乌斯反演

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6134

题意：

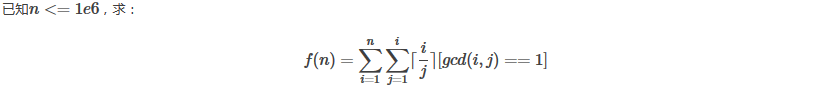
解法：

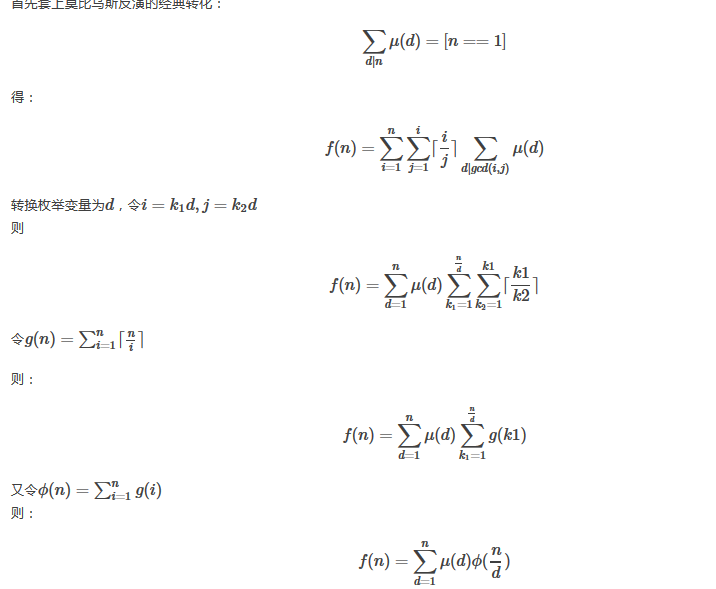
那么g(n)怎么求，我们尝试打表发现g(n)是有规律的，g(n)=g(n-1)+d(n-1)+1,其中d(i)表示i的因子个数，这个我们是可以通过线性筛O(n)处理出来的，之后再O(n)维护g(i)的前缀和，就可以在单组sqrt(n)的复杂度下得到答案了。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1e6+10;
const LL mod = 1e9+7;
bool check[maxn];
LL mu[maxn],d[maxn],sum[maxn],cnt[maxn];
int prime[maxn];
void Mobius()
{
    memset(check,false,sizeof(check));
    d[1]=mu[1]=1LL;
    int tot=0;
    for(int i=2; i<maxn; i++){
        if(!check[i]){
            prime[tot++]=i;
            d[i]=2;
            cnt[i]=1;
            mu[i]=-1;
        }
        for(int j=0; j<tot; j++){
            if((LL)i*prime[j]>maxn) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                d[i*prime[j]] = d[i]/(cnt[i]+1)*(cnt[i]+2);
                cnt[i*prime[j]] = cnt[i] + 1;
                mu[i*prime[j]]=0;
                break;
            }
            else{
                d[i*prime[j]]=d[i]<<1;
                cnt[i*prime[j]]=1;
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
    sum[1]=1;
    for(int i=2; i<maxn; i++){
        sum[i]=(sum[i-1]+d[i-1]+1)%mod;
    }
    for(int i=1; i<maxn; i++){
        sum[i]=(sum[i]+sum[i-1])%mod;
        mu[i]=(mu[i]+mu[i-1])%mod;
    }
}
int main()
{
    Mobius();
    int n;
    while(~scanf("%d",&n))
    {
        LL ans = 0;
        int last;
        for(int i=1; i<=n; i=last+1){
            last=n/(n/i);
            ans=(ans+(mu[last]-mu[i-1])%mod*sum[n/i]%mod)%mod;
        }
        ans = (ans+mod)%mod;
        printf("%lld
", ans);
    }
    return 0;
}