Description
我们讲一个悲伤的故事。
从前有一个贫穷的樵夫在河边砍柴。
这时候河里出现了一个水神,夺过了他的斧头,说:
“这把斧头,是不是你的?”
樵夫一看:“是啊是啊!”
水神把斧头扔在一边,又拿起一个东西问:
“这把斧头,是不是你的?”
樵夫看不清楚,但又怕真的是自己的斧头,只好又答:“是啊是啊!”
水神又把手上的东西扔在一边,拿起第三个东西问:
“这把斧头,是不是你的?”
樵夫还是看不清楚,但是他觉得再这样下去他就没法砍柴了。
于是他又一次答:“是啊是啊!真的是!”
水神看着他,哈哈大笑道:
“你看看你现在的样子,真是丑陋!”
之后就消失了。
樵夫觉得很坑爹,他今天不仅没有砍到柴,还丢了一把斧头给那个水神。
于是他准备回家换一把斧头。
回家之后他才发现真正坑爹的事情才刚开始。
水神拿着的的确是他的斧头。
但是不一定是他拿出去的那把,还有可能是水神不知道怎么偷偷从他家里拿走的。
换句话说,水神可能拿走了他的一把,两把或者三把斧头。
樵夫觉得今天真是倒霉透了,但不管怎么样日子还得过。
他想统计他的损失。
樵夫的每一把斧头都有一个价值,不同斧头的价值不同。总损失就是丢掉的斧头价值和。
他想对于每个可能的总损失,计算有几种可能的方案。
注意:如果水神拿走了两把斧头a和b,(a,b)和(b,a)视为一种方案。拿走三把斧头时,(a,b,c),(b,c,a),(c,a,b),(c,b,a),(b,a,c),(a,c,b)视为一种方案。
Input
第一行是整数N,表示有N把斧头。
接下来n行升序输入N个数字Ai,表示每把斧头的价值。
Output
若干行,按升序对于所有可能的总损失输出一行x y,x为损失值,y为方案数。
Sample Input
4
4
5
6
7
4
5
6
7
Sample Output
4 1
5 1
6 1
7 1
9 1
10 1
11 2
12 1
13 1
15 1
16 1
17 1
18 1
样例解释
11有两种方案是4+7和5+6,其他损失值都有唯一方案,例如4=4,5=5,10=4+6,18=5+6+7.
5 1
6 1
7 1
9 1
10 1
11 2
12 1
13 1
15 1
16 1
17 1
18 1
样例解释
11有两种方案是4+7和5+6,其他损失值都有唯一方案,例如4=4,5=5,10=4+6,18=5+6+7.
HINT
所有数据满足:Ai<=40000
题意:
给出 n个物品,价值为别为Xi且各不相同,现在可以取1个、2个或3个,问每种价值和有几种情况?顺序不同算一种。
解法:
显然是个母函数,A表示每种物品取一个的情况,B表示每种物品取二个的情况,C表示每种物品取三个的情况。用指数表示价值,系数表示该价值的个数,显然多项式相乘后指数会相加,系数会相乘,很容易就求出来了。
所以对于每种物品价值x,A[x]++,B[2*x]++,C[3*x]++。
如果取1个物品,答案就是A。
如果取2个物品,A^2中有重复的(x,x)的情况,所以答案为A^2-B。
如果去3个物品,A^3中可能有(x,x,x)(x,x,y)(x,y,x)(y,x,x)这几种重复的情况,而A*B能够求出所有形容(x,x,x)和(x,y,y)的情况数。(x,x,y)(x,y,x)(y,x,x)总的情况数=(x,y,y)*3,而A*B*3又会多减去了两次(x,x,x),所以要用C加回来。所以答案为A^3-3*B*A+2C。又由于顺序不同算一种情况,因为每种物品价值都不一样,情况(2)/2,情况(3)/6。
故总情况数量等于:
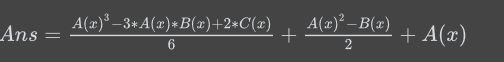
#include <bits/stdc++.h>
using namespace std;
const int maxn = 300000;
typedef long long LL;
const double PI = acos(-1.0);
typedef complex <double> Complex;
void rader(Complex *y, int len) {
for(int i = 1, j = len / 2; i < len - 1; i++) {
if(i < j) swap(y[i], y[j]);
int k = len / 2;
while(j >= k) {j -= k; k /= 2;}
if(j < k) j += k;
}
}
void fft(Complex *y, int len, int op) {
rader(y, len);
for(int h = 2; h <= len; h <<= 1) {
double ang = op * 2 * PI / h;
Complex wn(cos(ang), sin(ang));
for(int j = 0; j < len; j += h) {
Complex w(1, 0);
for(int k = j; k < j + h / 2; k++) {
Complex u = y[k];
Complex t = w * y[k + h / 2];
y[k] = u + t;
y[k + h / 2] = u - t;
w = w * wn;
}
}
}
if(op == -1) for(int i = 0; i < len; i++) y[i] /= len;
}
Complex a[maxn],b[maxn],c[maxn];
int n, len, x, m, mx;
int main()
{
scanf("%d", &n);
for(int i=0; i<n; i++){
scanf("%d", &x);
a[x]+=(1),b[2*x]+=(1),c[3*x]+=(1);
mx = max(mx, 3*x);
}
mx++;
len = 1;
while(len < mx*2){
len <<= 1;
}
m = len+1;
fft(a, len, 1);
fft(b, len, 1);
fft(c, len, 1);
Complex t2=(2),t3=(3),t6=(6);
for (int i=0;i<len;i++)
a[i]=(a[i]*a[i]*a[i]-t3*a[i]*b[i]+t2*c[i])/t6+(a[i]*a[i]-b[i])/t2+a[i];
fft(a, len, -1);
for(int i=1; i<m; i++){
LL num = (LL)(a[i].real()+0.5);
if(num!=0) printf("%d %lld
", i,num);
}
return 0;
}