LeetCode 84 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

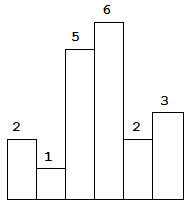
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

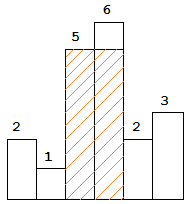
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

1. 万物皆可暴力 （2333,没想到 javascript 暴力下来，性能还阔以啊

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function(heights) {
  let len = heights.length;
  let area = 0;
  // 特判
  if(len === 0) return 0;
  for(let i = 0; i < len; i++) {
    let curHeight = heights[i];
    // 找到左边界
    let left = i;
    while(left > 0 && heights[left - 1] >= curHeight) left --;
    // 找到右边界
    let right = i;
    while(right < len - 1 && heights[right + 1] >= curHeight) right ++;
    area = Math.max(area, curHeight * (right - left + 1));
  }
  return area;
};

2. 使用单调栈

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function(heights) {
  // 特判
  if(heights.length === 0) return 0;
  // 矩形的最大面积
  let maxArea = 0;
  // 定义单调栈
  let stack = [];
  // 处理 heights
  heights = [0, ...heights, 0];
  // 遍历单调栈
  for(let i = 0; i < heights.length; i++) {
    // 当前 heights[i]与栈顶元素做比较，栈顶元素大才继续
    while(heights[i] < heights[stack[stack.length - 1]]) {
      // 保存栈顶元素的位置
      let stackTopIndex = stack.pop();
      // 比较出矩形的最大面积, 高度为上面出栈的 topIndex 的heights[stackTopIndex],宽度为当前 i 减去栈顶的下表 再减去 1
      maxArea = Math.max(maxArea, heights[stackTopIndex] * (i - stack[stack.length - 1] - 1));
    }
    // 把下表记录到 stack 里面
    stack.push(i);
  }
  return maxArea;
};