扩展欧几里得求乘法逆元

在开始之前我们先介绍3个定理：

1.乘法逆元（在维基百科中也叫倒数，当然是 mod p后的,其实就是倒数不是吗？）:

如果ax≡1 (mod p),且gcd(a,p)=1（a与p互质），则称a关于模p的乘法逆元为x。

2.费马小定理（定义来自维基百科）：

假如a是一个整数，p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）

它是欧拉定理的一个特殊情况（即

3.

扩展欧几里得

（定义来自维基百科）:

已知整数a、b，扩展欧几里得算法可以在求得a、b的最大公约数的同时，能找到整数x、y（其中一个很可能是负数），使它们满足贝祖等式。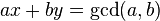

好了，在明白上面的定理后我们开始分析乘法逆元：ax≡1 (mod p) 这个等式用中文描述就是 a乘一个数x并模p等于1，即 a%p*x%p=res,res%p=1;看上去就是同余定理的一个简单等式- -。那么问题来了。

为什么可以用费马小定理来求逆元呢？

由费马小定理 a^p-1≡1(mod p) , 变形得 a*a^p-2≡1(mod p)，答案已经很明显了:若a,p互质,因为a*a^p-2≡1(mod p)且a*x≡1(mod p),则x=a^p-2(mod p),用快速幂可快速求之。

为什么可以用扩展欧几里得求得逆元？

我们都知道模就是余数，比如12%5=12-5*2=2，18%4=18-4*4=2。（/是程序运算中的除）

那么ax≡1 (mod p)即ax-yp=1.把y写成+的形式就是ax+py=1，为方便理解下面我们把p写成b就是ax+by=1。就表示x是a的模b乘法逆元，y是b的模a乘法逆元。然后就可以用扩展欧几里得求了。

知道逆元怎么算之后，那么乘法逆元有什么用呢？

做题时如果结果过大一般都会让你模一个数，确保结果不是很大，而这个数一般是1e9+7，而且这个数又是个素数，加减乘与模运算的顺序交换不会影响结果，但是除法不行。有的题目要求结果mod一个大质数，如果原本的结果中有除法，比如除以a,那就可以乘以a的逆元替代。（除一个数等于乘它的倒数，虽然这里的逆元不完全是倒数，但可以这么理解，毕竟乘法逆元就是倒数的扩展）。

 来源：https://www.cnblogs.com/dupengcheng/p/5487362.html