BM算法,全称是Boyer-Moore算法,1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了一种新的字符串匹配算法。
BM算法定义了两个规则:
1、坏字符规则:当文本串中的某个字符跟模式串的某个字符不匹配时,我们称文本串中的这个失配字符为坏字符,此时模式串需要向右移动,移动的位数 = 坏字符在模式串中的位置 - 坏字符在模式串中最右出现的位置。此外,如果"坏字符"不包含在模式串之中,则最右出现位置为-1。
2、好后缀规则:当字符失配时,后移位数 = 好后缀在模式串中的位置 - 好后缀在模式串上一次出现的位置,且如果好后缀在模式串中没有再次出现,则为-1。
关于坏字符规则和好后缀规则的具体讲解,以及怎么移动,可以查看阮一峰老师的详细讲解:http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
这里根据讲解画了两张图,方便自己理解坏字符规则:
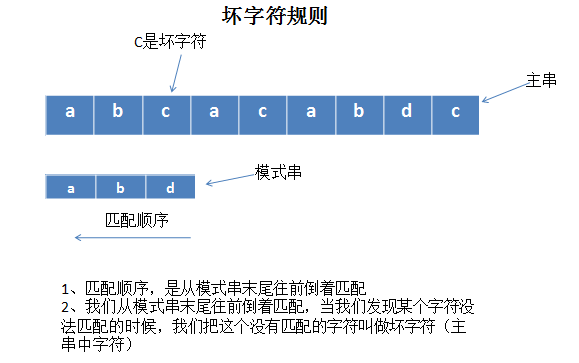
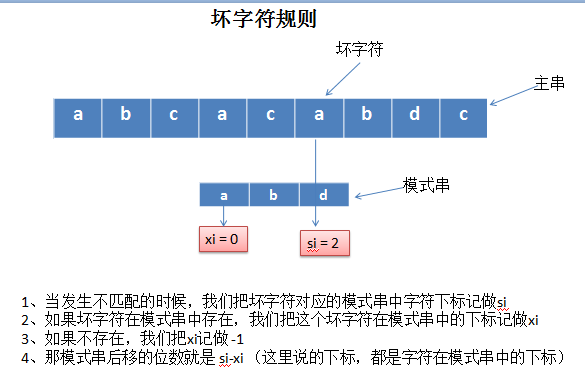

2019年11月14日15:38:41 修改
具体代码如下:
1 private static final int SIZE = 256; // 全局变量或者是局部变量 2 3 /** 4 * 坏字符规则哈希表构建方法 5 * 6 * @param b 7 * 模式串 8 * @param m 9 * 模式串的长度 10 * @param bc 11 * 散列表 12 */ 13 private void generateBC(char[] b, int m, int[] bc) { 14 for (int i = 0; i < SIZE; ++i) { 15 bc[i] = -1; // 初始化bc 16 } 17 18 for (int i = 0; i < m; ++i) { 19 int ascii = (int) b[i]; // 计算b[i]的ASCII值 20 bc[ascii] = i; 21 } 22 } 23 24 /** 25 * 好后缀规则构建哈希表 26 * 27 * @param b 28 * 模式串 29 * @param m 30 * 模式串长度 31 * @param suffix 32 * suffix数组的下标 k,表示后缀子串的长度, 33 * 下标对应的数组值存储的是,在模式串中跟好后缀{u}相匹配的子串{u*}的起始下标值 34 * @param prefix 35 * 记录模式串的后缀子串是否能匹配模式串的前缀子串 36 */ 37 private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) { 38 for (int i = 0; i < m; ++i) { // 初始化 39 suffix[i] = -1; 40 prefix[i] = false; 41 } 42 43 for (int i = 0; i < m - 1; ++i) { 44 int j = i; 45 int k = 0; // 公共后缀子串长度 46 while (j >= 0 && b[j] == b[m - 1 - k]) { // 与b[0, m-1]求公共后缀子串 47 --j; 48 ++k; 49 suffix[k] = j + 1; // j+1表示公共后缀在b[0,i]中的起始下标 50 } 51 if (j == -1) { 52 prefix[k] = true; // 如果公共后缀子串也是模式串的后缀子串 53 } 54 } 55 } 56 57 /** 58 * 完整的BM算法 好后缀+坏字符 59 * 60 * @param a 61 * 主串 62 * @param n 63 * 主串的长度 64 * @param b 65 * 模式串 66 * @param m 67 * 模式串的长度 68 * @return 69 */ 70 public int bm(char[] a, int n, char[] b, int m) { 71 int[] bc = new int[SIZE]; 72 generateBC(b, m, bc); // 构建坏字符哈希表 73 int[] suffix = new int[m]; 74 boolean[] prefix = new boolean[m]; 75 generateGS(b, m, suffix, prefix); // 构建好字符哈希表 76 int i = 0; // j 表示主串与模式串匹配的第一个字符 77 while (i < n - m) { 78 int j = 0; 79 for (j = m - 1; j >= 0; --j) {// 模式串从后向前匹配 80 if (a[i + j] != b[j]) { 81 break; // 坏字符串 82 } 83 } 84 if (j < 0) { 85 return i;// 匹配成功,返回主串和模式串第一个匹配字符的位置 86 } 87 int x = j - bc[(int) a[i + j]]; 88 int y = 0; 89 if (j < m - 1) { // 如果有好后缀的话 90 y = moveByGS(j, m, suffix, prefix); 91 } 92 i = i + Math.max(x, y); 93 } 94 return -1; 95 } 96 97 private int moveByGS(int j, int m, int[] suffix, boolean[] prefix) { 98 int k = m - 1 - j; // 好后缀的长度 99 if (suffix[k] != -1) { 100 return j - suffix[k] + 1; 101 } 102 for (int r = j + 2; r <= m - 1; ++r) { 103 if (prefix[m - r] == true) { 104 return r; 105 } 106 } 107 return m; 108 }
现在再看BM算法,原来之前自己是一点也没弄懂!只是当做文章简单读了一遍,阿西吧!
首先,那个坏字符的散列表的构建就没有弄懂:
1、为什么在散列表数组中要初始化每一个值为-1?
这里是在坏字符匹配的时候,如果主串与模式串中字符没有匹配上(把坏字符在模式串中下标记做xi),此时的xi=-1
2、你有没有考虑过模式串中的相同的字符的ASCII码是相同的,那样循环处理的话,只是记录模式串中相同字符中最后面的那个字符的下标,没有问题吗?
这个是没有问题的!这里无非有两种情况,就是坏字符与非坏字符:
坏字符:因为是从后向前倒序匹配,只需要知道后面的字符下标,就可以计算出移动距离
非坏字符:需要去寻找坏字符或者使用好后缀规则
2019年11月14日15:34:37 修改
此大部分内容来自极客时间专栏,王争老师的《数据结构与算法之美》