有向无环图
任务的执行有依赖关系,如下图所示:
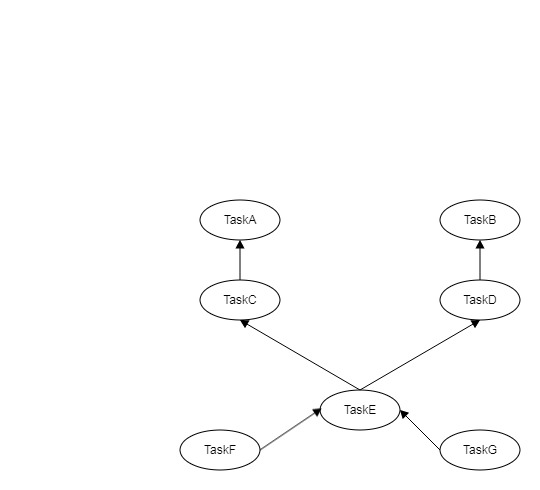
可以使用DAG(有向无环图)来维护这种依赖关系;
定义task
@Data
@NoArgsConstructor
public class NodeTask {
private String id;
private Set<String> dependences = Sets.newConcurrentHashSet(); //依赖的taskID
public NodeTask(String id) {
this.id = id;
}
public NodeTask addDependence(String nodeTaskId) {
this.dependences.add(nodeTaskId);
return this;
}
}
Graph
package com.ssslinppp.graph.directd;
import com.google.common.collect.Lists;
import com.google.common.collect.Maps;
import com.google.common.collect.Queues;
import com.google.common.graph.GraphBuilder;
import com.google.common.graph.MutableGraph;
import java.util.List;
import java.util.Map;
import java.util.Queue;
public class TaskGraph {
private MutableGraph<NodeTask> taskGraph = GraphBuilder.directed().allowsSelfLoops(false).build();
/**
* 转换节点任务为Graph
*
* @param nodeTasks
*/
public void parseNodeTasksToGraph(Map<String, NodeTask> nodeTasks) {
for (NodeTask nodeTask : nodeTasks.values()) {
if (!taskGraph.nodes().contains(nodeTask)) {
taskGraph.addNode(nodeTask);
}
for (String dependence : nodeTask.getDependences()) {
taskGraph.putEdge(nodeTask, nodeTasks.get(dependence));
}
}
}
/**
* 判断是否为DAG(Directed Acyclic Graph)有向无环图
* <p>
* 算法思路:
* <ul>
* <li>1. 根据"拓扑排序"算法判断:拓扑排序之后,若还剩有点,则表示有环</li>
* <li>2. 拓扑排序算法:找到图中所有入度为0的点,放入序列,删除这些点和以这些点为出度的边,再找所有入度为0的点,依次循环</li>
* </ul>
*
* @return
*/
public boolean isDAGraph() {
Map<String, Integer> nodeInDegreeMap = Maps.newHashMap();
Queue<NodeTask> queue = Queues.newArrayDeque();
List<String> topologicalSortList = Lists.newArrayList(); //拓扑排序列表维护
// 获取所有入度为0的节点
for (NodeTask nodeTask : taskGraph.nodes()) {
int indegree = taskGraph.inDegree(nodeTask);
nodeInDegreeMap.put(nodeTask.getId(), indegree);
if (indegree == 0) {
queue.add(nodeTask);
topologicalSortList.add(nodeTask.getId());
}
}
while (!queue.isEmpty()) {
NodeTask preNode = queue.poll(); //获取并删除
for (NodeTask successorNode : taskGraph.successors(preNode)) {
int indegree = nodeInDegreeMap.get(successorNode.getId());
if (--indegree == 0) {//-1:等效删除父节点以及相应的边
queue.offer(successorNode); //insert
topologicalSortList.add(successorNode.getId());
}
nodeInDegreeMap.put(successorNode.getId(), indegree);
}
}
System.out.println("拓扑排序(topologicalSortList):" + topologicalSortList);
if (topologicalSortList.size() != taskGraph.nodes().size()) {
return false;
}
return true;
}
/**
* 打印Graph中task的依赖关系
*/
public void print() {
System.out.println("=============NodeTask count: " + taskGraph.nodes().size());
for (NodeTask nodeTask : taskGraph.nodes()) {
System.out.println("-------- NodeTask: " + nodeTask.getId() + "--------");
System.out.print("Dependent on: ");
taskGraph.successors(nodeTask).forEach((v) -> System.out.print(v.getId() + ", "));
System.out.println();
System.out.print("all predecessors: ");
taskGraph.predecessors(nodeTask).forEach((v) -> System.out.print(v.getId() + ", "));
System.out.println();
System.out.println();
}
}
}
Test
package com.ssslinppp.graph.directd;
import com.google.common.collect.Maps;
import org.junit.Test;
import java.util.Map;
public class TaskGraphTest {
/**
* 测试依赖关系
*/
@Test
public void testDependence() {
Map<String, NodeTask> nodeTaskMap = Maps.newConcurrentMap();
NodeTask nodeTaskA = new NodeTask("nodeTaskA");
NodeTask nodeTaskB = new NodeTask("nodeTaskB");
NodeTask nodeTaskC = new NodeTask("nodeTaskC").addDependence("nodeTaskA");
NodeTask nodeTaskD = new NodeTask("nodeTaskD").addDependence("nodeTaskB");
NodeTask nodeTaskE = new NodeTask("nodeTaskE").addDependence("nodeTaskC").addDependence("nodeTaskD");
NodeTask nodeTaskF = new NodeTask("nodeTaskF").addDependence("nodeTaskE");
NodeTask nodeTaskG = new NodeTask("nodeTaskG").addDependence("nodeTaskE");
nodeTaskMap.put(nodeTaskA.getId(), nodeTaskA);
nodeTaskMap.put(nodeTaskB.getId(), nodeTaskB);
nodeTaskMap.put(nodeTaskC.getId(), nodeTaskC);
nodeTaskMap.put(nodeTaskD.getId(), nodeTaskD);
nodeTaskMap.put(nodeTaskE.getId(), nodeTaskE);
nodeTaskMap.put(nodeTaskF.getId(), nodeTaskF);
nodeTaskMap.put(nodeTaskG.getId(), nodeTaskG);
TaskGraph taskGraph = new TaskGraph();
taskGraph.parseNodeTasksToGraph(nodeTaskMap);
System.out.println("======== DAG(有向无环图)判断 ===========");
if (taskGraph.isDAGraph()) {
System.out.println("is DAG");
} else {
System.out.println("Not DAG");
}
System.out.println("=============== print ===========");
taskGraph.print();
}
/**
* 判断是否为有向无环图
*/
@Test
public void testDAG() {
// E依赖D, D依赖B, B依赖E ==>(B,E,G)为一个环
Map<String, NodeTask> nodeTaskMap = Maps.newConcurrentMap();
NodeTask nodeTaskA = new NodeTask("nodeTaskA");
NodeTask nodeTaskB = new NodeTask("nodeTaskB");
// nodeTaskB.addDependence("nodeTaskE"); // 在这里控制是否有环,进行测试
NodeTask nodeTaskC = new NodeTask("nodeTaskC").addDependence("nodeTaskA");
NodeTask nodeTaskD = new NodeTask("nodeTaskD").addDependence("nodeTaskB");
NodeTask nodeTaskE = new NodeTask("nodeTaskE").addDependence("nodeTaskC").addDependence("nodeTaskD");
NodeTask nodeTaskF = new NodeTask("nodeTaskF").addDependence("nodeTaskE");
NodeTask nodeTaskG = new NodeTask("nodeTaskG").addDependence("nodeTaskE");
nodeTaskMap.put(nodeTaskA.getId(), nodeTaskA);
nodeTaskMap.put(nodeTaskB.getId(), nodeTaskB);
nodeTaskMap.put(nodeTaskC.getId(), nodeTaskC);
nodeTaskMap.put(nodeTaskD.getId(), nodeTaskD);
nodeTaskMap.put(nodeTaskE.getId(), nodeTaskE);
nodeTaskMap.put(nodeTaskF.getId(), nodeTaskF);
nodeTaskMap.put(nodeTaskG.getId(), nodeTaskG);
TaskGraph taskGraph = new TaskGraph();
taskGraph.parseNodeTasksToGraph(nodeTaskMap);
System.out.println("======== DAG(有向无环图)判断 ===========");
if (taskGraph.isDAGraph()) {
System.out.println("It is DAG");
} else {
System.out.println("Not DAG");
}
}
}
pom
<dependencies>
<dependency>
<groupId>org.springframework.boot</groupId>
<artifactId>spring-boot-starter</artifactId>
</dependency>
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>23.0</version>
</dependency>
<dependency>
<groupId>org.projectlombok</groupId>
<artifactId>lombok</artifactId>
<optional>true</optional>
</dependency>
<dependency>
<groupId>org.springframework.boot</groupId>
<artifactId>spring-boot-starter-test</artifactId>
<scope>test</scope>
</dependency>
</dependencies>