1.素数
###(1)朴素素数测试: 对于一个数n,n要么是素数要么有一个小于等于$sqrt{x}$的约数 那么$O(sqrt{x})$暴力判断即可
但是n很大怎么办呢 ###(2)米勒拉宾素数判定: 首先要知道费马小定理 欧拉也一块证了吧 欧拉定理:若a,p互质那么$a^{phi(n)}=1(mod n) 费马小定理:若p为质数,那么$a^(p-1)equiv1(mod p)$(0
伪素数测试 
Miller_Rabin
定理:

方法:


狄利克雷卷积:
对于数论函数f,g,定义其狄利克雷卷积为((f*g)(n)=sum_{dmidn}f(d)g(frac{n}{d}))
满足:
1 交换律(f*g=g*f)
2 结合律((f*g)*h=f*(g*h))
3 分配率(f*(g+h)=f*g+f*h)
例题:

解:

莫比乌斯反演
莫比乌斯函数:
定义: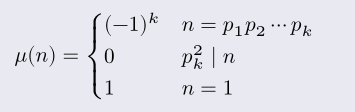
性质:
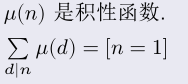
公式
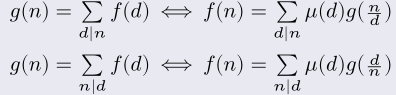
公式证明
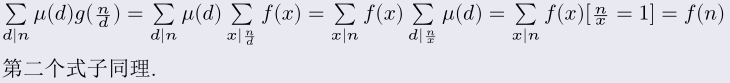
例题:
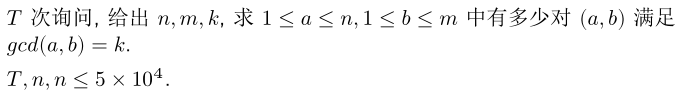
解:
