bzoj2752: [HAOI2012]高速公路(road)

题目链接

bzoj2752: [HAOI2012]高速公路(road)

题解

首先将每次修改和询问的r减1，把线段权值转化为点权值。
然后使用总和/总次数的方式计算期望。
第i个点(l≤i≤r)，它被选中的次数为((i−l+1)∗(r−i+1))所以所求即为

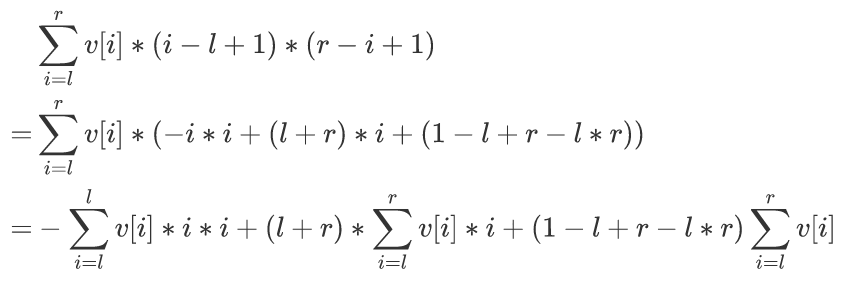
线段树维护(v[i]∗i∗i、v[i]∗i、v[i])的区间和即可。

代码

#include<bits/stdc++.h> 
using namespace std; 
#define LL long long 
#define int long long
const int  maxn = 200007; 
inline LL read() { 
    LL x = 0,f = 1; 
    char c = getchar(); 
    while(c < '0' || c > '9'){if(c == '-')f = -1;  c = getchar();} 
    while(c <= '9' && c >= '0')x = x * 10 + c - '0',c = getchar(); 
    return x * f; 
} 
#define ls rt << 1 
#define rs rt << 1 | 1 

struct Segtree{ 
    int l,r; 
    LL sum[5],tag; 
    Segtree (){ 
        sum[0] = sum[1] = sum[2] = 0; 
        tag = 0; 
    } 
} t[maxn << 2]; 
LL pre[maxn][3],ans[3]; 
inline LL Pre (Segtree a,int i) { 
    return pre[a.r][i] - pre[a.l - 1][i]; 
} 
inline void updata(int rt) { 
     for(int i = 0;i < 3;++ i) t[rt].sum[i] = t[ls].sum[i] + t[rs].sum[i]; 
} 
inline void pushdown(int rt) { 
    if(t[rt].tag == 0) return; 
    t[ls].tag += t[rt].tag; 
    t[rs].tag += t[rt].tag; 
    for(int i=0;i<3;++i) { 
        t[ls].sum[i] += t[rt].tag * Pre(t[ls],i); 
        t[rs].sum[i] += t[rt].tag * Pre(t[rs],i); 
    } 
    t[rt].tag = 0; 
} 
void build(int rt,int l,int r) { 
    t[rt].l = l,t[rt].r = r;  
    if(l == r) return;  
    int mid = l + r >> 1 ;  
    build(ls,l,mid); 
    build(rs,mid+1,r); 
    return; 
} 
void modify(int rt,int tl,int tr,LL x) { 
    int l = t[rt].l,r = t[rt].r; 
    pushdown(rt);
    if(l >= tl && tr >= r) { 
        t[rt].tag += x; 
        for(int i = 0;i < 3;++ i) t[rt].sum[i] += x * Pre(t[rt],i); 
        return; 
    }  
    int mid = l + r >> 1; 
    if(tl <= mid) modify(ls,tl,tr,x); 
    if(tr >  mid) modify(rs,tl,tr,x); 
    updata(rt); 
    return;  
} 
LL query(int rt,int tl,int tr,int i) { 
    int l = t[rt].l,r = t[rt].r; 
    pushdown(rt);
    if(l >= tl && r <= tr) return t[rt].sum[i];  
    int mid = l + r >> 1;LL ret = 0;   
    if(tl <= mid) ret += query(ls,tl,tr,i); 
    if(tr >  mid) ret += query(rs,tl,tr,i); 
    return ret; 
} 
LL gcd(LL a,LL b) { 
    return b == 0ll ? a : gcd(b,a % b); 
} 
 main() { 
    for(int i = 1;i <= 100000;++ i) { 
        pre[i][0] = pre[i-1][0] + 1ll; 
        pre[i][1] = pre[i - 1][1] + (LL) i; 
        pre[i][2] = pre[i - 1][2] + (LL) i * i;  
    } 
    int n = read(),m = read();  
    build(1,1,n-1); 
    char ch[10]; 
    while(m --) { 
        scanf("%s",ch + 1); 
        int  l = read(),r = read(); 
        if(ch[1] == 'C') { 
            LL x = read();  
            modify(1,l,r-1,x); 
        } else {  
            for(int i = 0;i < 3;++ i) ans[i] = query(1,l,r - 1,i);   
            LL a = (r - l * r) * ans[0] + (l + r - 1) * ans[1] - ans[2];  
            LL b = ((1ll * (r - l + 1) * (r - l)) >> 1),c = gcd(a,b);   
           	cout<<a / c<<"/"<<b / c<<endl; 
        } 
    }  
    return 0; 
}