# 背包专题

背包专题

目录

• 背包专题
  • 01背包
  • 完全背包
  • 多重背包
  • 分组背包

01背包

N个物品，容量为V的背包，每个物品只能使用一次

for(int i=1;i<=N;i++)cin>>st[i].v>>st[i].w;

for(int i=1;i<=N;i++)
    for(int j=1;j<=V;j++){
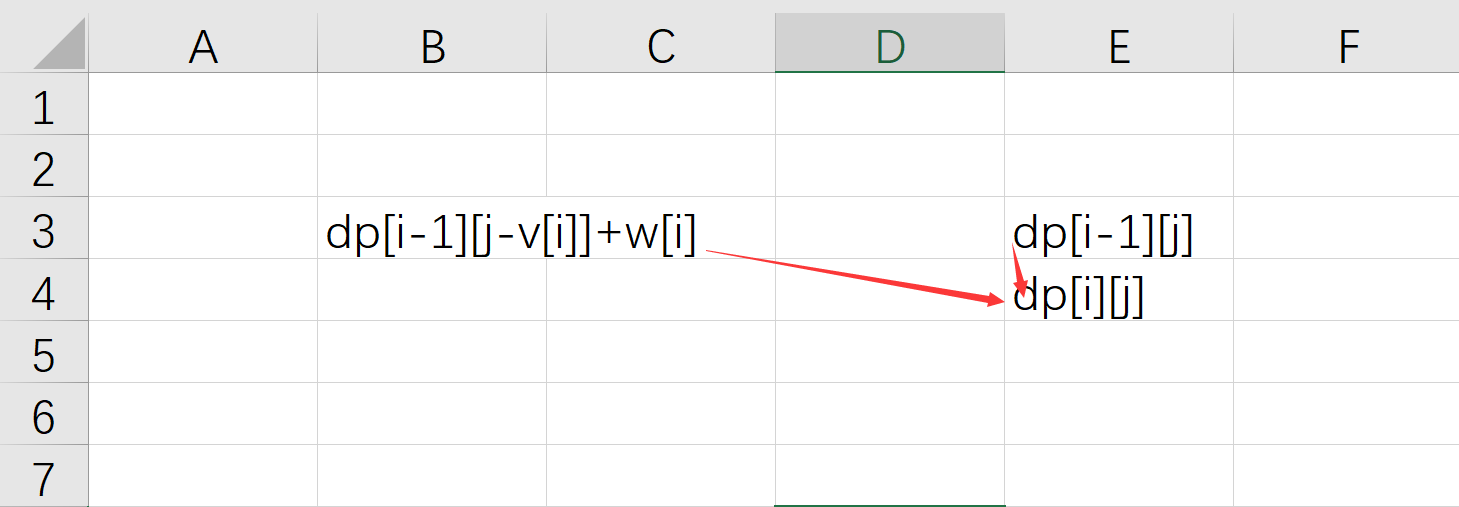
        dp[i][j]=dp[i-1][j];
        if(j-st[i].v>=0) dp[i][j]=max(dp[i][j],dp[i-1][j-st[i].v]+st[i].w);
    }

cout<<dp[N][V]<<endl;

dp数组优化成一维：

背包容量逆序递推，因为要使用到上一层的数据

for(int i=1;i<=N;i++)cin>>st[i].v>>st[i].w;

for(int i=1;i<=N;i++)
    for(int j=V;j>=st[i].v;j--)
        dp[j]=max(dp[j],dp[j-st[i].v]+st[i].w);

cout<<dp[V]<<endl;

完全背包

N个物品，容量为V的背包，每个物品有无限个可以使用

for(int i=1;i<=N;i++)cin>>st[i].v>>st[i].w;

for(int i=1;i<=N;++i)
    for(int j=1;j<=V;j++)
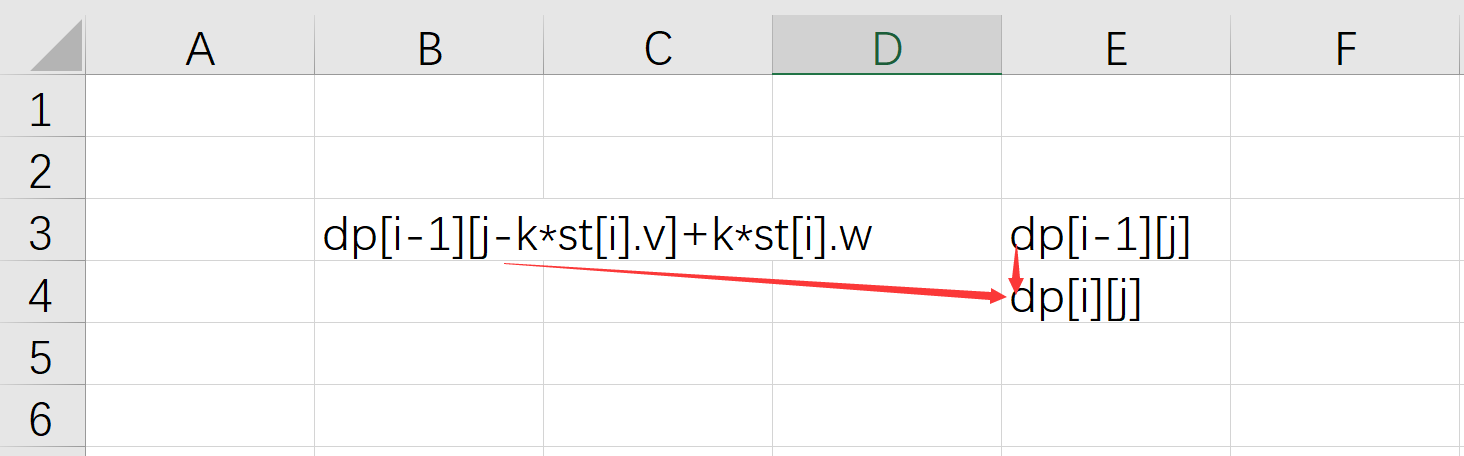
        for(int k=0;k*st[i].v<=j;k++)
            dp[i][j]=max(dp[i][j],dp[i-1][j-k*st[i].v]+k*st[i].w);

cout<<dp[N][V]<<endl;

将枚举每个物品取用的数量k转移到当前物品使用数量为k-1的状态：

背包容量正序递推，使用到的数据是当前物品的前一种数量下的值

for(int i=1;i<=N;i++)cin>>st[i].v>>st[i].w;

for(int i=1;i<=N;i++)
    for(int j=0;j<=V;j++) {
        dp[i][j]=dp[i-1][j];
        if(j-st[i].v>=0)dp[i][j] = max(dp[i][j], dp[i][j - st[i].v] + st[i].w);
    }

cout<<dp[N][V];

类似01背包，将dp数组优化成一维：

for(int i=1;i<=N;i++)cin>>st[i].v>>st[i].w;

for(int i=1;i<=N;i++)
    for(int j=st[i].v;j<=V;j++) {
        dp[j] = max(dp[j], dp[j - st[i].v] + st[i].w);
    }
cout<<dp[V];

多重背包

N个物品，容量为V的背包，每个物品有s[i]个

将每种物品的s[i]个拆分打包成不同的组，以二进制的形式分组，最后如果无法拆成2的整数次幂，则单独成一组。

例如：(22=1+2+4+8+7=(1111)_2+(7)_{10})

这些组的不同组合可以拼凑出0-s[i]，并且每个组只能选一次。这样就转化成了01背包，拆分之后最后物品种类数为(N*logs)

时间复杂度：(O(NVlogS))

cin>>N>>V;
idx=1; //idx记录下标，作用和链式前向星存储中的idx一样
for(int i=1;i<=N;i++){
    cin>>vv>>ww>>sum;
    k=1;
    while(k<=sum){
        ++idx;
        v[idx]=k*vv;
        w[idx]=k*ww;
        sum-=k;k<<=1;
    }
    if(sum){//处理最后无法拆成2的整数次幂
        ++idx;
        v[idx]=sum*vv;
        w[idx]=sum*ww;
    }
}

N=idx;
for(int i=1;i<=N;i++)
    for(int j=V;j>=v[i];j--)
        dp[j]=max(dp[j],dp[j-v[i]]+w[i]);

cout<<dp[V]<<endl;

分组背包

N类物品，容量为V的背包，每类物品有若干种物品，每类物品中只能选一个。

例如：水果类有1个苹果，1个香蕉，1个西瓜，但是只能买一种水果。

对于每类物品，枚举选择哪一种物品。

cin>>N>>V;
for(int i=1;i<=N;i++){
    cin>>s[i];
    for(int j=1;j<=s[i];j++)cin>>v[i][j]>>w[i][j];
}

for(int i=1;i<=N;i++)
    for(int j=V;j>=0;j--)
        for(int k=1;k<=s[i];k++)
            if(v[i][k]<=j)
                dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);

cout<<dp[V];