题解——Dynamic Rankings(树状数组+主席树)
这道题可以整体二分过,但我写了树套树
而且这个外层树不是那么明显
题目传送门
给定一个含有n个数的序列a[1],a[2],a[3]……a[n],程序必须回答这样的询问:对于给定的i,j,k,在a[i],a[i+1],a[i+2]……a[j]中第k小的数是多少(1≤k≤j-i+1),并且,你可以改变一些a[i]的值,改变后,程序还能针对改变后的a继续回答上面的问题。你需要编一个这样的程序,从输入文件中读入序列a,然后读入一系列的指令,包括询问指令和修改指令。
第一行有两个正整数n(1≤n≤100000),m(1≤m≤100000)。分别表示序列的长度和指令的个数。
第二行有n个数,表示a[1],a[2]……a[n],这些数都小于10^9。接下来的m行描述每条指令,每行的格式是下面两种格式中的一种。 Q i j k 或者 C i t
Q i j k (i,j,k是数字,1≤i≤j≤n, 1≤k≤j-i+1)表示询问指令,询问a[i],a[i+1]……a[j]中第k小的数。
C i t (1≤i≤n,0≤t≤10^9)表示把a[i]改变成为t。
简化题意
带单点修改的区间第K小(大)
关于静态第K大(主席树)
默认各位是会主席树的,只是复习一下,具体讲解在代码中
就是对原数组离散化,每个状态为一颗新的权值线段树,维护一个类似于前缀和的东西,由于每次相同部分很多,考虑用可持久化线段树节约空间(每次只开一条链)。
AC code(静态):
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1000005 ;
inline int read(){
int s = 0,w = 1;char g = getchar();while(g<'0'||g>'9'){if(g=='-')w*=-1;g = getchar();}
while(g>='0'&&g<='9'){s = s*10+g-'0';g = getchar();}return s*w;
}
int b[ MAXN ] , a [ MAXN ] , root[ MAXN ] ;
int N , M , cnt = 0 ;
struct Segment{
int ls , rs , num ;
}t[ MAXN<<5 ] ;
void copyNode( int x , int y ){
t[ x ].ls = t[ y ].ls , t[ x ].rs = t[ y ].rs , t[ x ].num = t[ y ].num+1 ;
}
void build( int p , int l , int r ){//初始建树
t[ p ].num = 0 ;
if( l == r )return ;
int mid = ( l+r )>>1 ;
build( t[ p ].ls = ++cnt , l , mid ) ;
build( t[ p ].rs = ++cnt , mid+1 , r ) ;
}
int New_made( int las , int l , int r , int pos ){//新建,las为上一状态
int p = ++cnt ;
copyNode( p , las ) ;//新建的链深=树深,别想多了
if( l == r )return p ;
int mid = ( l+r )>> 1 ;
if( pos <= mid )t[ p ].ls = New_made( t[ p ].ls , l , mid , pos ) ;//二分查找
else t[ p ].rs = New_made( t[ p ].rs , mid+1 , r , pos ) ;
return p ;
}
int ask( int x , int y , int l , int r , int rank ){
if( l == r )return l ;
int mid = (l+r)>>1 ;
int dif = t[ t[x].ls ].num - t[ t[y].ls ].num ;
if( rank <= dif )ask( t[ x ].ls , t[ y ].ls , l , mid , rank ) ;//值域上二分
else ask( t[ x ].rs , t[ y ].rs , mid+1 , r , rank-dif ) ;
}
int main(){
N = read() , M = read() ;//平时不用register了
for( int i = 1 ; i <= N ; ++i )b[ i ] = a[ i ] = read() ;
sort( b+1 , b+N+1 ) ;
int tot = unique( b + 1 , b + 1 + N ) - b - 1 ;//自带的去重 ,返回的是数组的尾地址
build( root[0] = ++cnt , 1 , tot ) ; //root , l , r
for( int i = 1 ; i <= N ; ++i ){//nlogn,等效Hash
int pos = lower_bound( b+1 , b+tot+1 , a[ i ] ) - b ;
root[ i ] = New_made( root[i-1] , 1 , tot , pos ) ; // 上一版本root , l , r , pos
}
for( int i = 1 ; i <= M ; ++i ){
int m1 = read() , m2 = read() , m3 = read() ;
int t = ask( root[ m2 ] , root[ m1-1 ] , 1 , tot , m3 ) ; //前缀和思想
printf("%d
",b[ t ] ) ;
}
return 0 ;
}
关于动态第K大(树状数组套主席树)
上面每棵树都是一个历史状态,即第i棵树代表了第i个状态时序列 1~i 所对应的值域线段树树上形态,就是维护了一个前缀和。
然后,带修改,如果单纯的修改前缀包含该位置的所有树,明显T飞的。
然后,某些神仙们并不满足,既然每棵树和序列上的一个前缀区间可以相互对应,那为何不能用树状数组像维护 n 个数的序列一样维护 n 棵主席树呢?(请回顾下图)
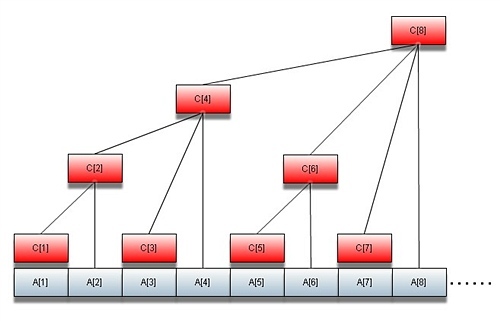
上图中的 c[1]~c[8] 都会对应一颗主席树。然后,每次修改是 log 棵数一起修改 , 每次查询仍然是两个状态, 但每个状态都会由 log 棵树一起组成 。 所以.....时间和空间复杂度都是 NlogN^2 。
具体的我写在代码中了(参考来参考去,最后终于写了一个好点的板子)
#include<bits/stdc++.h>
using namespace std ;
const int MAXN = 100005 ;//log 16
inline int read(){
int s = 0,w = 1;char g = getchar();while(g<'0'||g>'9'){if(g=='-')w*=-1;g = getchar();}
while(g>='0'&&g<='9'){s = s*10+g-'0';g = getchar();}return s*w;
}
int b[ MAXN*2 ] , a[ MAXN ] , root[ MAXN*18 ] ;
int N , M , cnt = 0 , totx = 0 , toty = 0 , xx[ 18 ] , yy[ 18 ] , tot = 0 ;
int opa[ MAXN ] , opb[ MAXN ] , opc[ MAXN ] ;
char op[ 20 ] ;
struct Segment{
int ls , rs , num ;
}t[ MAXN*324 ] ; // 空间log^2
void copyNode( int x , int y , int z ){
if( x == 0 )return ;
t[ x ].ls = t[ y ].ls , t[ x ].rs = t[ y ].rs , t[ x ].num = t[ y ].num + z ;
}
int New_made( int las , int l , int r , int pos , int val ){
int p = ++cnt ;
copyNode( p , las , val ) ;// las = 0 一样
if( l == r )return p ;
int mid = (l+r)>>1 ;
if( pos <= mid )t[ p ].ls = New_made( t[ p ].ls , l , mid , pos , val ) ;
else t[ p ].rs = New_made( t[ p ].rs , mid+1 , r , pos , val ) ;
return p ;
}
int query( int l , int r , int k ){//实现log棵树同时移动
if( l == r ) return l;
int sum = 0 , mid = (l+r)/2; // sum是 log个 状态差 的和
for( int i=1;i<=totx;i++) sum += t[t[ xx[i] ].ls].num ;
for( int i=1;i<=toty;i++) sum -= t[t[ yy[i] ].ls].num ;
if( sum >= k ){//二分,log棵树同时向下进入左区间或右区间,请读者自行脑补
for(int i=1;i<=totx;i++) xx[i]=t[ xx[i] ].ls;
for(int i=1;i<=toty;i++) yy[i]=t[ yy[i] ].ls;
return query( l , mid , k ) ;
}else{
for(int i=1;i<=totx;i++) xx[i]=t[ xx[i] ].rs;
for(int i=1;i<=toty;i++) yy[i]=t[ yy[i] ].rs;
return query( mid+1 , r , k-sum ) ;
}
}
void add( int x , int val ){//log次增加,就是多开了log条链
int pos = lower_bound( b+1 , b+tot+1 , a[ x ] ) - b ;
for( int i = x ; i <= N ; i += i&-i )
root[ i ] = New_made( root[ i ] , 1 , tot , pos , val ) ; // 上一版本root , l , r , pos
}
int ask( int x , int y , int z ){// 找出每次修改对应的log棵树
totx = toty = 0 ;
for( int j = y ; j ; j -=j&(-j) ) xx[++totx]=root[j];
for( int j = x - 1 ; j ; j -=j&(-j) ) yy[++toty]=root[j];
int ans = query( 1 , tot , z ) ;
return b[ans] ;
}
int main(){
N = read() , M = read() , tot = N ;
for( int i = 1 ; i <= N ; ++i )b[ i ] = a[ i ] = read() ;
for( int i = 1 ; i <= M ; ++i ){
scanf("%s",op);
opa[ i ] = read() , opb[ i ] = read() ;//离线后,方便进行离散化
if( op[ 0 ]=='Q' )opc[ i ] = read() ;
else b[ ++tot ] = opb[ i ] ;
}
sort( b+1 , b+tot+1 ) ;
tot = unique( b+1 , b+tot+1 )-b-1 ; //离散化,同静态
for( int i = 1 ; i <= N ; ++i )add( i , 1 ) ;
for( int i = 1 ; i <= M ; ++i )
if( opc[ i ] )printf("%d
",ask( opa[ i ] , opb[ i ] , opc[ i ]) ) ;
else {
add( opa[ i ] , -1 ) ;//修改,树上对应的个数 -1
a[ opa[ i ] ] = opb[ i ] ;//序列上对应修改
add( opa[ i ] , 1 ) ;//个数+1
}
return 0 ;
}
然后,记得树的空间要开log^2倍,别像ssw02一样挂了。