机器学习实战---线性回归（更好的使用正规方程求解）

回顾梯度下降和正规方程：https://www.cnblogs.com/ssyfj/p/12788147.html

一：正规方程解法（最小二乘法）

（一）加载数据

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(filename):
    dataSet = np.loadtxt(filename)
    m,n = dataSet.shape
    data_X = dataSet[:,0:n-1]
    data_Y = dataSet[:,n-1]
    return data_X,data_Y

（二）使用正规方程求解参数向量

def standRegres(data_X,data_Y):
    XTX = data_X.T@data_X
    XT = data_X.T
    if np.linalg.det(XTX) == 0: #linalg.det用于求解方阵行列式，如果求解的行列式值=0，则不可以求逆
        print("data X cann`t inverse")
        return
    W = np.linalg.inv(XTX)@XT@data_Y
    return W

（三）载入数据，测试结果

data_X,data_Y = loadDataSet("ex0.txt")
W = standRegres(data_X,data_Y)

plt.figure()
plt.scatter(data_X[:,1].flatten(),data_Y.flatten(),c="green",marker="o")

x = np.linspace(0,1,100)
print(W)
y = W[0]+W[1]*x
plt.plot(x,y)

plt.show()

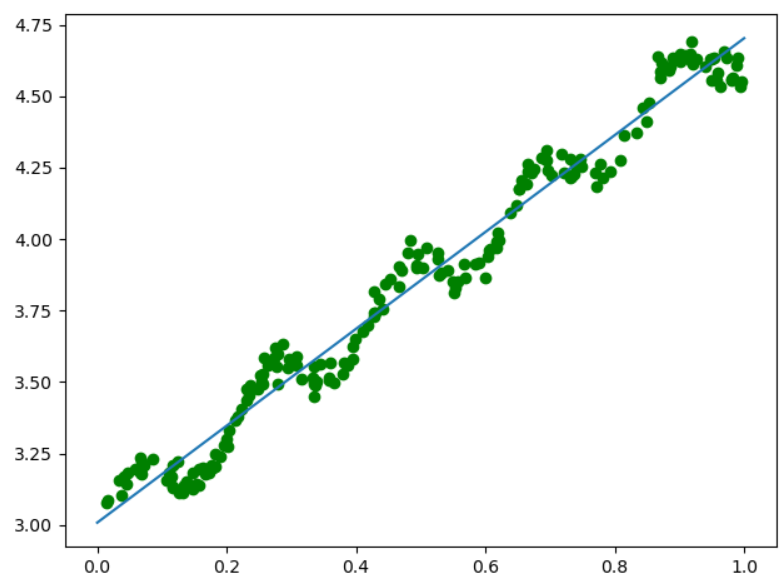
二：局部加权避免欠拟合

补充：高斯分布https://www.cnblogs.com/ssyfj/p/12940077.html

解释见机器学习实战。通过W矩阵的对角线上设置不同的数值，表示对不同的数据样本数值不同的权重（与支持向量机中的核类似）。

对于预测值距离标签值越近的点，我们设置的权重越大，越远设置越小。这里我们使用的是高斯核：其对应的权重如下：

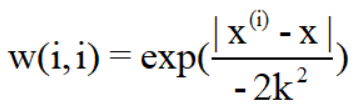
从公式中，我们可以看到k，即方差影响了高斯分布的收敛速度，当k越小时，下降速度越快，因此考虑的样本数（局部、附近）也就越少，故而对于当前局部样本数据点的拟合直线也就越符合当前的局部数据点（而非全局）。当我们迭代访问完成全部数据后，会发现拟合的模型为折线，而非直线，因为折线的每一段都是对局部样本集的最好拟合，而直线是对全局数据点的拟合。

所以当我们设置的k值越小，高斯收敛越快，涉及的局部样本点越少，折线段数越多，导致对全局样本的拟合程度超过我们预期的拟合模型，变为过拟合，所以合理的选取k值，是一个重要的问题。

（一）导入数据

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(filename):
    dataSet = np.loadtxt(filename)
    m,n = dataSet.shape
    data_X = dataSet[:,0:n-1]
    data_Y = dataSet[:,n-1]
    return data_X,data_Y

（二）实现局部加权函数预测每个样本点的结果

def lwlr(testPoint,data_X,data_Y,k=1.0):    #求解当前样本点的权重W，从而获取当前样本点的预测值
    m,n = data_X.shape
    W = np.eye(m)

    for i in range(m):  #对每一个样本点都求解其权重
        diff = testPoint - data_X[i,:]  #样本点差距，是个向量，还要进行处理
        W[i,i] = np.exp(diff@diff.T/(-2*k**2))

    XTWX = data_X.T@W@data_X
    XT = data_X.T
    if np.linalg.det(XTWX) == 0: #linalg.det用于求解方阵行列式，如果求解的行列式值=0，则不可以求逆
        print("data X cann`t inverse")
        return
    W = np.linalg.inv(XTWX)@XT@W@data_Y
    return testPoint@W.T  #返回当前样本点的预测值

（三） 测试函数

def lwlrTest(testPoint,data_X,data_Y,k=1.0):
    yPred = np.zeros(data_Y.shape)
    
    for i in range(data_X.shape[0]):
        yPred[i] = lwlr(testPoint[i], data_X, data_Y, k)

    return yPred

（四）绘制图像

data_X,data_Y = loadDataSet("abalone.txt")
yPred = lwlrTest(data_X,data_X,data_Y,1.0)
#注意：因为绘制折线图是从左向右逐步绘制的，所以我们的数据需要进行排序处理，将data_X和yPred进行排序之后处理
SortIdx = data_X[:,1].argsort(0)    #小到大排序，获取索引
Sort_X = data_X[SortIdx]

plt.figure()
plt.scatter(data_X[:,1].flatten(),data_Y.flatten(),c="green",marker="o")
plt.plot(Sort_X[:,1].flatten(),yPred[SortIdx].flatten(),c="r")

plt.show()

（五）当k分别为1，0.01，0.003时的拟合结果

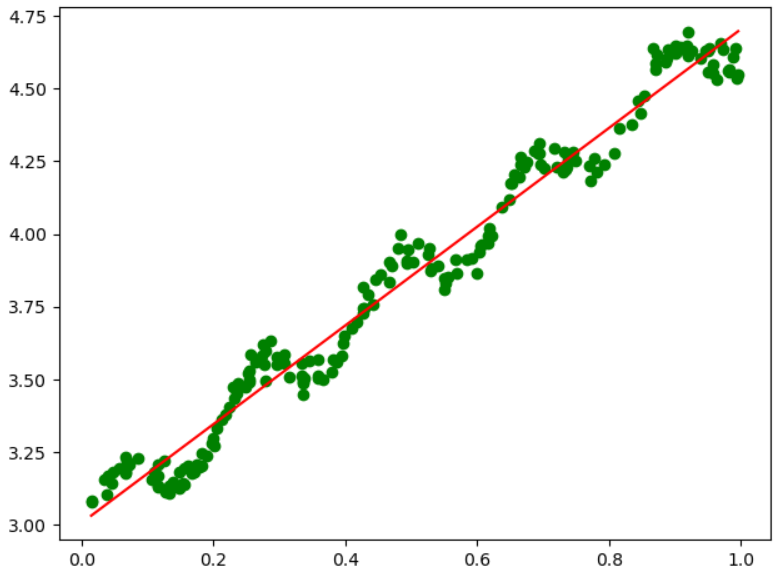
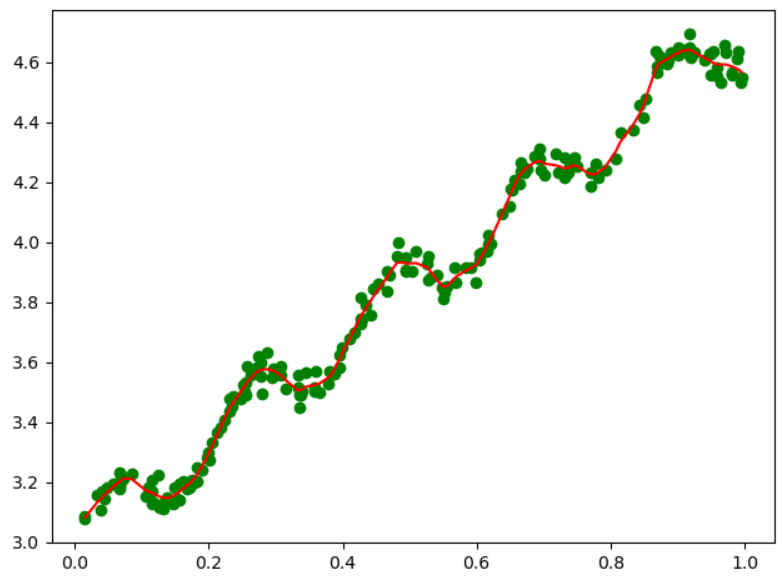
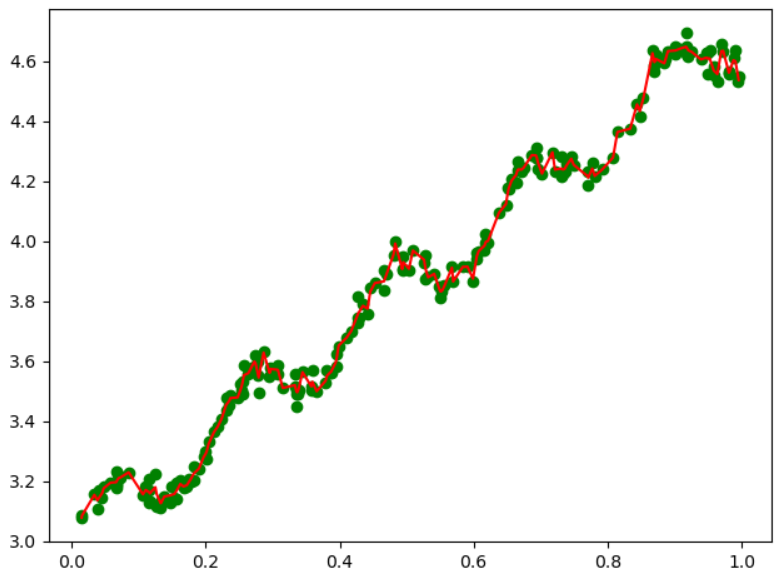
（六）预测鲍鱼年龄

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(filename):
    dataSet = np.loadtxt(filename)
    m,n = dataSet.shape
    data_X = dataSet[:,0:n-1]
    data_Y = dataSet[:,n-1]
    return data_X,data_Y

def lwlr(testPoint,data_X,data_Y,k=1.0):    #求解当前样本点的权重W，从而获取当前样本点的预测值
    m,n = data_X.shape
    W = np.eye(m)

    for i in range(m):  #对每一个样本点都求解其权重
        diff = testPoint - data_X[i,:]  #样本点差距，是个向量，还要进行处理
        W[i,i] = np.exp(diff@diff.T/(-2*k**2))

    XTWX = data_X.T@W@data_X
    XT = data_X.T
    if np.linalg.det(XTWX) == 0: #linalg.det用于求解方阵行列式，如果求解的行列式值=0，则不可以求逆
        print("data X cann`t inverse")
        return
    W = np.linalg.inv(XTWX)@XT@W@data_Y
    return testPoint@W.T  #返回当前样本点的预测值

def lwlrTest(testPoint,data_X,data_Y,k=1.0):
    yPred = np.zeros(data_Y.shape)
    for i in range(data_X.shape[0]):
        yPred[i] = lwlr(testPoint[i], data_X, data_Y, k)

    return yPred

误差计算

def rssError(yArr,yHatArr):
    return ((yArr-yHatArr)**2).sum()

训练集中的拟合程度（误差查看）

data_X,data_Y = loadDataSet("abalone.txt")

yPred01 = lwlrTest(data_X[0:99],data_X[0:99],data_Y[0:99],0.1)
print(rssError(data_Y[0:99],yPred01))

yPred1 = lwlrTest(data_X[0:99],data_X[0:99],data_Y[0:99],1)
print(rssError(data_Y[0:99],yPred1))

yPred10 = lwlrTest(data_X[0:99],data_X[0:99],data_Y[0:99],10)
print(rssError(data_Y[0:99],yPred10))

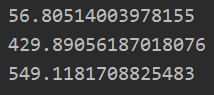
测试集拟合程度（误差查看） 

yPred01 = lwlrTest(data_X[100:199],data_X[0:99],data_Y[0:99],0.1)
print(rssError(data_Y[100:199],yPred01))

yPred1 = lwlrTest(data_X[100:199],data_X[0:99],data_Y[0:99],1)
print(rssError(data_Y[100:199],yPred1))

yPred10 = lwlrTest(data_X[100:199],data_X[0:99],data_Y[0:99],10)
print(rssError(data_Y[100:199],yPred10))

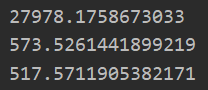
总感觉这样测试有问题....,因为实际中测试中还是使用了测试集数据去拟合数据 

三：缩减系数法

岭回归等同于就是L2正则化，而对于L2正则化的问题

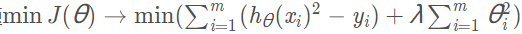
就是约束问题： 

同样lasso回归，也是L1正则化， 通过约束项依旧可以达到缩减系数的目的。所以说常用的缩减系数法包括岭回归和lasso回归两种方法.

一般缩减系数常用于大量系数中，对于书籍后面乐购估价（不想做）中，由于选取特征过少，所以结果和最小二乘法几乎一致，没有缩减必要性

四：岭回归

岭回归和LASSO回归（一）

岭回归和LASSO回归（二）

（一）数据导入

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(filename):
    dataSet = np.loadtxt(filename)
    m,n = dataSet.shape
    data_X = dataSet[:,0:n-1]
    data_Y = dataSet[:,n-1]
    return data_X,data_Y

（二）岭回归算法实现

def ridgeRegres(data_X,data_Y,lam=0.2): #计算回归系数
    XTX = data_X.T@data_X
    new_dataX = XTX+np.eye(data_X.shape[1])*lam

    if np.linalg.det(new_dataX) == 0:
        print("can`t inverse")
        return
    W = np.linalg.inv(new_dataX)@data_X.T@data_Y
    return W

（三）测试不同lamda选取

def ridgeTest(data_X,data_Y):   #查看lamda选择值的表现
    #数据归一化
    newData_X = (data_X - np.mean(data_X,0))/np.var(data_X,0)
    newData_Y = data_Y - np.mean(data_Y,0)

    lamdaNums = 30
    W = np.zeros((lamdaNums,newData_X.shape[1]))
    print(W.shape)
    for i in range(lamdaNums):
        Wi = ridgeRegres(newData_X,newData_Y,np.exp(i-10))
        W[i] = Wi.T
    return W

（四）绘制lamda选取图像

data_X,data_Y = loadDataSet("abalone.txt")
W = ridgeTest(data_X,data_Y)

plt.figure()
plt.plot(W)
plt.show()

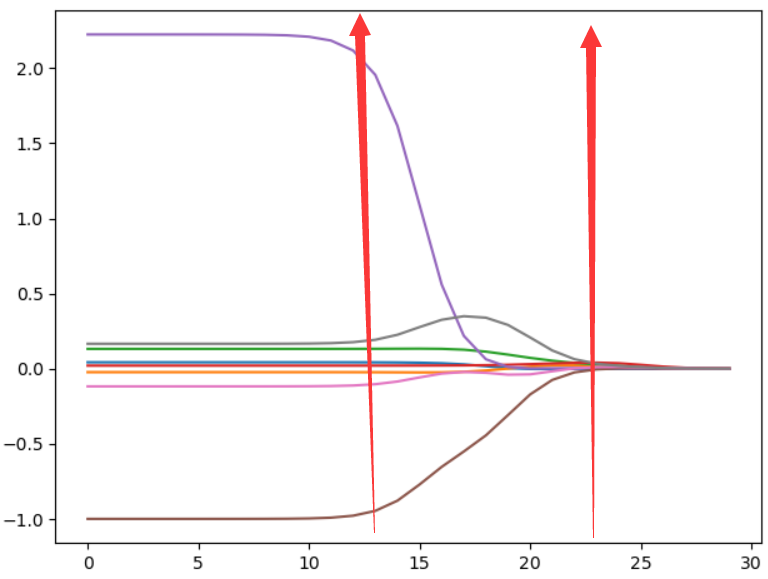
当λ为0时，结果跟普通意义的多元线性回归的最小二乘解完全一样；
在λ较小时，各个回归系数比较大；
当λ增大时，各个回归系数取值迅速减小，即从不稳定趋于稳定。
上图中类似喇叭形状的岭迹图，一般存在多重共线性。（因为有8个特征值，所以回归系数之也有8个，对应8条曲线）

λ选择：一般通过观察，选择喇叭口附近的值，此时各个回归系数趋于稳定，而且预测值与实际值的平方误差不太大。
但是也不能选太大的λ，因为，上图中，貌似随着λ的增大，回归系数的取值大小趋于稳定，但是实际对应的平方误差已经非常大了。
为了定量地找到最佳参数值，还需要进行交叉验证。另外，要判断哪些变量对结果预测最有影响力，可以观察上图中对应系数的大小

建议使用交叉验证进行比较获取λ取值比较好

（五）总结

Ridge回归在不抛弃任何一个变量的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但这会使得模型的变量特别多，模型解释性差。

有没有折中一点的办法呢？即又可以防止过拟合，同时克服Ridge回归模型变量多的缺点呢？有，这就是下面说的Lasso回归。

（六）补充岭回归和最小二乘法区别

https://www.zhihu.com/question/28221429?sort=created

五：lasso回归

Lasso回归和岭回归的同和异

Lasso回归和岭回归的同和异

Lasso回归使得一些系数变小，甚至还是一些绝对值较小的系数直接变为0，因此特别适用于参数数目缩减与参数的选择，因而用来估计稀疏参数的线性模型。

但是Lasso回归有一个很大的问题，导致我们需要把它单独拎出来讲，就是它的损失函数不是连续可导的，由于L1范数用的是绝对值之和，导致损失函数有不可导的点。

也就是说，我们的最小二乘法，梯度下降法，牛顿法与拟牛顿法对它统统失效了。那我们怎么才能求有这个L1范数的损失函数极小值呢？

接下来介绍两种全新的求极值解法：坐标轴下降法（coordinate descent）和最小角回归法（ Least Angle Regression， LARS）。

....

太烦了，以后用到再说（https://www.cnblogs.com/wmx24/p/9555219.html）

六：实现前向逐步线性回归

（一）代码实现

import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(filename):
    dataSet = np.loadtxt(filename)
    m,n = dataSet.shape
    data_X = dataSet[:,0:n-1]
    data_Y = dataSet[:,n-1]
    return data_X,data_Y

def rssError(yArr,yHatArr): #求解平方和误差
    return ((yArr-yHatArr)**2).sum()

def stageWise(data_X,data_Y,eps=0.01,numIt = 100):   #后两个传参是缩放系数和迭代次数
    #数据归一化
    newData_X = (data_X - np.mean(data_X,0))/np.var(data_X,0)
    newData_Y = data_Y - np.mean(data_Y,0)
    newData_Y = np.array([newData_Y]).T #注意：这里一定需要进行转置，否则后面的求解平方误差会出错
    m,n = data_X.shape
    #初始化我们要返回的权重矩阵，与迭代次数和特征数有关
    ReturnW = np.zeros((numIt,n))
    ws = np.zeros((n,1))
    # print(rssError())
    wsTest = ws.copy()  #设置副本
    wsMax = ws.copy()   #设置副本
    for i in range(numIt):  #按要求进行次数迭代，下面对每一个特征都进行一遍处理(但是每一次只更新最优的那个特征）
        print(ws.T)
        lowestError = np.inf  # 设置最低误差为正无穷　　本轮迭代中对因变量变化最大（使得预计值与真实值越接近）的这个特征值的系数；
        for j in range(n):  #对每一个特征都进行一遍处理
            for k in [-1,1]:    #进行增大或者减少比较平方误差
                wsTest = ws.copy()  #不对原始数据修改
                wsTest[j] += eps*k  #进行指定特征值的增加和减少
                yTest = newData_X@wsTest   #获取更新了特征值以后的预测值
                rssErr = rssError(newData_Y,yTest)
                if rssErr < lowestError:    #注意：由于使用的是副本，所以对于k,是对增加、减少、不变这三个方向进行对比，获取最小平方误差
                    lowestError = rssErr    #更新最小损失
                    wsMax = wsTest  #临时存储当前最优权值
        print(lowestError)
        ws = wsMax.copy()   #通过一轮迭代，上面对所有特征进行了一遍处理（增加、减少、不变），来获取目前最优（平方误差最小）权重向量
        ReturnW[i,:] = ws.T #记录这一次的结果（每一次结果的平方误差都会）　　获取的都是本轮变化量最大的值
    return ReturnW

data_X,data_Y = loadDataSet("abalone.txt")
print(data_X)
print(data_Y)
returnW = stageWise(data_X,data_Y,0.001,5000)

plt.figure()
plt.plot(returnW)
plt.show()

增加迭代次数如0.001，5000，可以得到和最小二乘近似的结果。

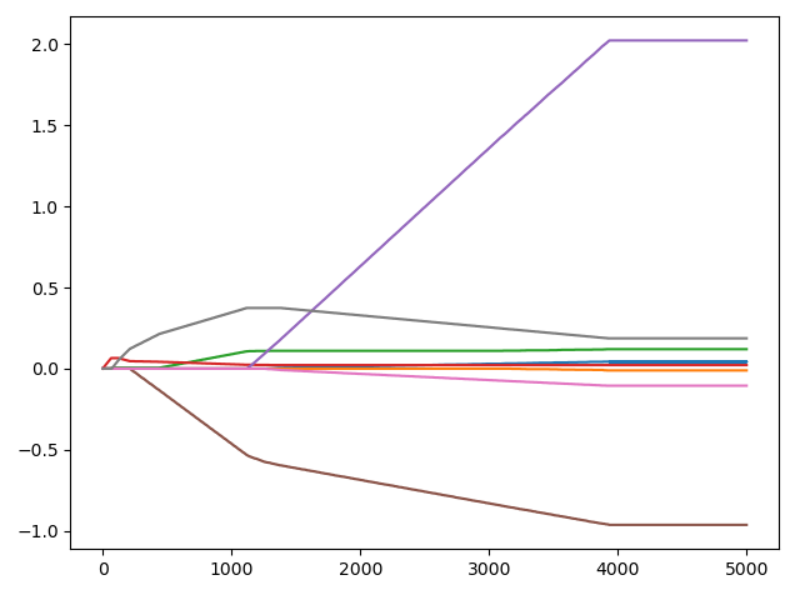
（二）结论

returnW = stepWise(data_X,data_Y,0.01,200)

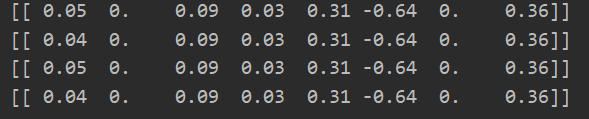
可见w1和w6对目标值无影响，这两个特征值可以不需要，减少步长。

逐步线性回归优点：构建一个模型后，利用本算法找出重要的特征，及时停止对不重要特征的收集