数据结构（一）线性表双向链表

（一）定义

双向链表是在单链表的每个结点中，再设置一个纸箱其前驱结点的指针域

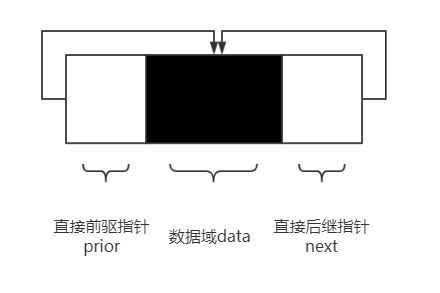
（二）结点结构

typedef struct Node
{
    ElemType data;
    struct Node* prior;    //直接前驱指针
    struct Node* next;    //直接后继指针
}Node;

typedef struct Node* CLinkList;

（三）双向链表结构

双向循环链表

带有头结点的空链表

带有头结点的数据链表

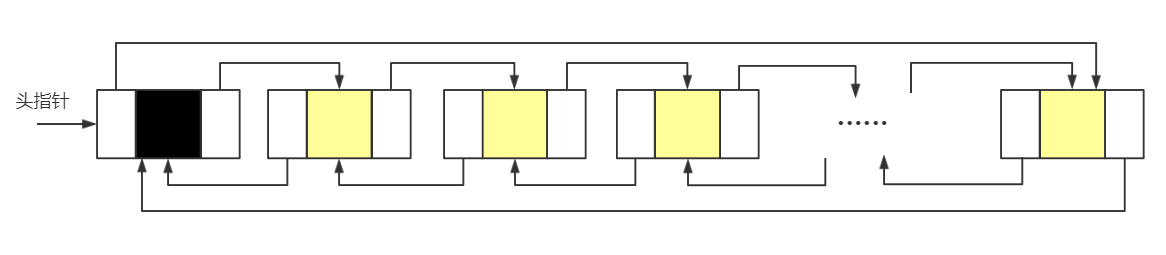
对于非循环的，直接将头结点的直接前驱指针置为空，将尾结点的直接后驱结点置为空即可

（四）实现双向链表

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef char ElemType;
typedef int Status;

typedef struct Node
{
    ElemType data;
    struct Node* prior;    //直接前驱指针
    struct Node* next;    //直接后继指针
}Node;

typedef struct Node* DLinkList;

//四个基本操作，初始化，清空，获取长度，是否为空
Status InitList(DLinkList* Dl);
Status ClearList(DLinkList* Dl);
int GetLength(DLinkList Dl);
Status EmptyList(DLinkList Dl);

//四个插入，程序，删除操作
Status GetElem(DLinkList Dl, int i, ElemType* e);
int LocateElem(DLinkList Dl, ElemType e);
Status InsertList(DLinkList* Dl, int i, ElemType e);
Status DeleteList(DLinkList* Dl, int i, ElemType* e);

//打印链表
void PrintList(DLinkList Dl, int i);

int main()
{
    DLinkList dbList;
    ElemType e='A';
    int i = 0;
    
    InitList(&dbList);//初始化链表
    
    for (; i < 26;i++)    //插入数据
    {
        //InsertList(&dbList, -1, e + i);    //尾插法
        InsertList(&dbList, GetLength(dbList)+1, e + i);    //头插法
    }

    PrintList(dbList, 3);
    PrintList(dbList, -3);

    system("pause");
    return 0;
}


//四个基本操作，初始化，清空，获取长度，是否为空
//创建一个带有头结点的双向链表
Status InitList(DLinkList* Dl)
{
    *Dl = (DLinkList)malloc(sizeof(Node));
    if (*Dl == NULL)
        return ERROR;
    (*Dl)->next = (*Dl)->prior = (*Dl);    //都指向头结点，虽然这里数据data为char，也是可以存储链表长度的，但是这里不使用
    return OK;
}

//清空双向链表,头结点也释放掉
Status ClearList(DLinkList* Dl)
{
    DLinkList Dlist = *Dl;
    DLinkList q;

    if (Dlist == NULL)
        return ERROR;

    //先将尾结点的next指针置为空，一会作为判断循环退出条件
    Dlist->prior->next = NULL;
    while (Dlist)
    {
        q = Dlist;
        Dlist = Dlist->next;
        free(q);
    }

    return OK;
}

//获取链表长度,不含头结点，使用一条单向指针域即可
int GetLength(DLinkList Dl)
{
    DLinkList cur = Dl->next;
    int length = 0;
    while (cur!=Dl)
    {
        cur = cur->next;
        length++;
    }
    return length;
}

//判断是否链表为空，判断头结点一个指针是否指向自己就可以
Status EmptyList(DLinkList Dl)
{
    if (Dl->prior == Dl)
        return TRUE;
    return FALSE;
}

//四个插入，程序，删除操作
//根据索引获取数据，支持双向索引
Status GetElem(DLinkList Dl, int i, ElemType* e)
{
    int j = 0;
    DLinkList cur = Dl;
    if (e == NULL||i==0)
        return ERROR;
    for (; j < abs(i);j++)
    {
        if (i < 0)
            cur = cur->prior;
        else
            cur = cur->next;
    }
    *e = cur->data;
    return OK;
}

//按照元素进行查找，单向正向查找
int LocateElem(DLinkList Dl, ElemType e)
{
    DLinkList cur = Dl->next;
    int index=1;
    while (cur->data != e&&cur != Dl)
    {
        cur = cur->next;
        index++;
    }
    if (cur == Dl)
        return 0;
    return index;
}

//支持双向插入
Status InsertList(DLinkList* Dl, int i, ElemType e)
{
    DLinkList cur = *Dl;
    DLinkList newNode;
    int j = 0;
    if (*Dl == NULL || abs(i) > GetLength(*Dl) + 1 || i == 0)
        return ERROR;
    for (; j < abs(i);j++)    //找到他的后一个节点，一会向前推
    {
        if (i < 0)
            cur = cur->prior;
        else
            cur = cur->next;
    }

    //创建一个新的结点
    newNode = (DLinkList)malloc(sizeof(Node));
    newNode->data = e;

    if (i<0)
    {
        newNode->next = cur->next;
        newNode->prior = cur;
        cur->next->prior = newNode;
        cur->next = newNode;
    }
    else
    {
        newNode->next = cur;
        newNode->prior = cur->prior;
        cur->prior->next = newNode;
        cur->prior = newNode;
    }
    return OK;
}

//支持双向删除
Status DeleteList(DLinkList* Dl, int i, ElemType* e)
{
    DLinkList cur = *(Dl);
    DLinkList oldNode;
    int j = 0;
    if (*Dl == NULL || abs(i) > GetLength(*Dl) || i == 0 || e == NULL)
        return ERROR;
    for (; j < abs(i); j++)    //找到要删除的结点
    {
        if (i < 0)
            cur = cur->prior;
        else
            cur = cur->next;
    }
    //赋值
    *e = cur->data;
    oldNode = cur;
    //开始交换指针顺序
    oldNode->prior->next = oldNode->next;
    oldNode->next->prior = oldNode->prior;
    free(oldNode);
    return OK;
}


//打印链表,支持双向打印，其实在main方法中稍微调整传入的结点也可以实现
void PrintList(DLinkList Dl, int i)
{
    DLinkList cur = Dl;
    DLinkList start;
    int j = 0;

    if (i==0)    //若是输入0，按照正向找到第一个结点进行输出即可
        cur = cur->next;

    for (; j < abs(i); j++)    //找到要开始打印的最开始那个结点
    {
        if (i < 0)
            cur = cur->prior;
        else
            cur = cur->next;
    }
    start = cur;    //找到最开始打印的那个结点
    while (cur->next!=start)    //进行判断结点
    {
        if (cur!=Dl)    //不打印头结点
            printf("%c ", cur->data);
        cur = cur->next;
    }
    if (cur != Dl)
        printf("%c", cur->data);
    printf("
");
}

（五）打印预览

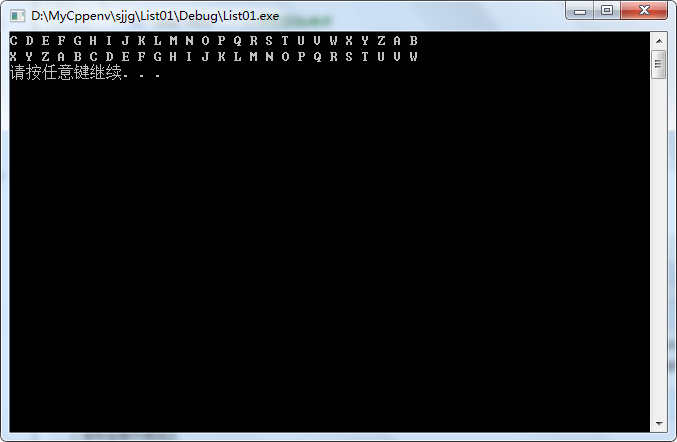
（六）总结

双向链表相对于单链表来说，要复杂些，多了个直接前驱指针，对于初入，删除考虑的指针交换需要格外小心。而且占用空间也增加了。
但是他有良好的对称性，是对于某个结点的前后结点的操作，带来了方便，提高了算法时间性能。也就是使用空间来换取时间。
原来单链表要寻找某个结点的前一个节点的时间复杂度是O(n),使用双向链表去查找前一个节点的时间复杂度是O(1)