2017-10-1719:26:55
01背包是dp入门经典问题,问题的原型是这样的:
给定n个物品,每个物品都有一定的价值和体积 , 你有一个容积为V 的背包 , 你要用这个背包装价值尽量大的物品(毕竟白捡,自然是捡的越多越好)。
每件物品只有两种选择: 选 或是 不选 因此这个问题被称为01背包(两个状态)
如果暴力的枚举每个物品的状态,那么每种状态有n次选择,一共有2^n个状态,时间复杂度太高/
实际上 , 之前枚举的状态可以用来简化后面的选择。
确定一个状态:d[ i ][ j ] 表示用容积为j的背包 处理完前i个物品能的到的最大价值
状态转移: 对于每个物品都有两个选择(选 or 不选) 那么 对于第i个物品 d[ i ] [ j ] = max( d[ i - 1 ] [ j ] , d[ i - 1 ] [ j - v [ i ] ] + w [ i ] ) // j from v[i] to V
//前者为不选第i个物品 ,后者是选第i个物品 v[i] 和 w[i] 分别代表 第i个物品的 体积 和 价值
举个例子:有5个物品 价值分别为 {2,2,6,5,4} 体积分别为{6,3,5,4,6} 状态转移的表
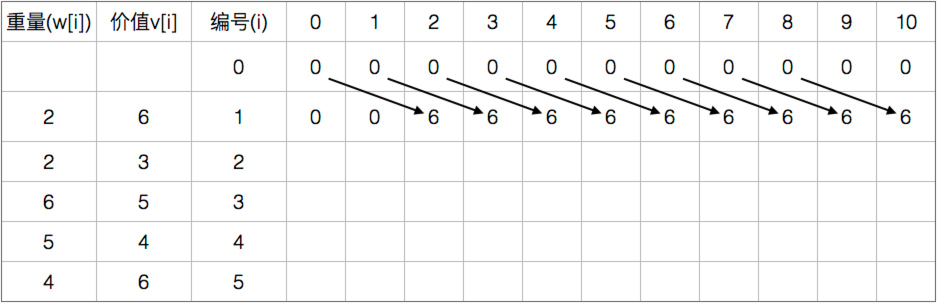
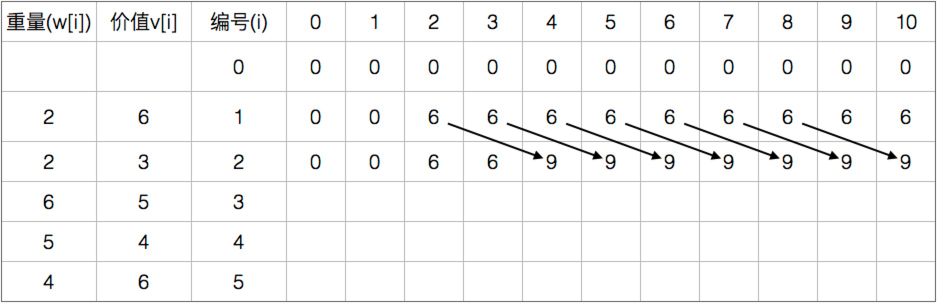
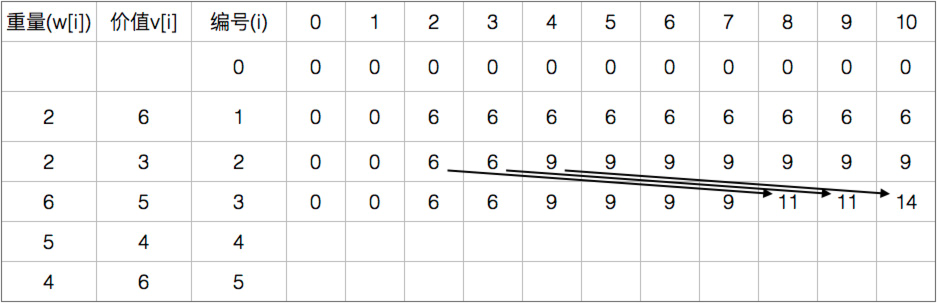
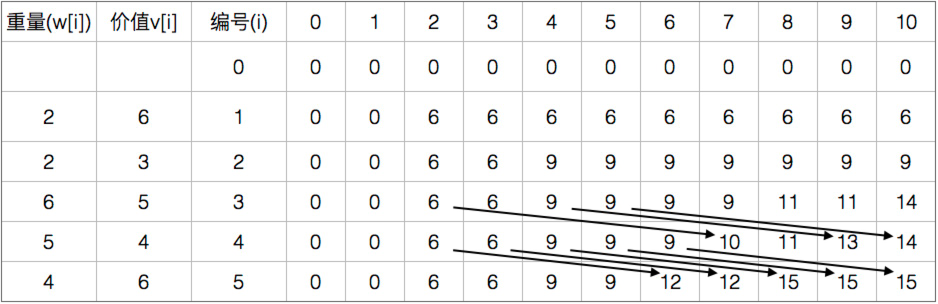
01背包的代码:
1 for(int i=1;i<=n;i++) 2 { 3 for(int j=v[i];j<=V;j++) 4 d[i][j]=max( d[i-1][j], d[i-1][j-v[i] ] +w[i] ); 5 }
这个代码的空间复杂度是V*n 状态转移的过程中只有d[i] 和d[i-1] 发生了转移 d[i] 是d[i-1] 的后一个状态
可以用一个一维数组来保存dp的状态 d[j] = max(d[ j ] , d[ j - v[ i ] ] + w[ i ] );
每次更新 都是 用体积较小的先更新 , 如果用 从前向后的更新方式 会出现一个物品被用多次的情况
所以更新的顺序是 从后向前更新
for(int i=1;i<=n;i++) { for(int j=V;j>=v[i];j--) d[j]=max(d[j] , d[j- v[i] ] +w[i]); }
空间复杂度为 O(N)
完全背包 是01背包的问题的变形 , 区别在于 每件物品的数量是无限的 , 这个问题和01背包的解法几乎完全一样
状态转移: d[ j ] = max ( d[ j ] , d [ j - c * v[ i ] ] +c * w [ i ] );
区别在于每件物品选了几件
1 for(int i=1;i<=n;i++)
2 {
3 for(int j=v[i] ; j<V;j++)
4 d[j] = max ( d [ j ] , d [ j - v [ i ] ] + w [ i ] ) ;
5 }
多重背包 : 指每种物品都有一定的数量 。 可以将其当成01背包来做 物品的数目太多时 如果枚举每件物品时间会花费很长
可以把物品拆分成若干个物品 , 比如说 把10个重量为 1 的物品拆成 1个重量为1的、1个重量为2的、1个重量为4的、一个重量为3的物品 共logn个物品 且这些物品可以组合成重量在1~n的任一物品。
这样相比第一种方式 多了log级别的优化