上一章主要描述了ID3算法的的原理,它是以信息熵为度量,用于决策树节点的属性选择,每次优选信息量最多
的属性,以构造一颗熵值下降最快的决策树,到叶子节点处的熵值为0,此时每个叶子节点对应的实例集中的实例属于同一类。
理想的决策树有三种:
1.叶子节点数最少
2.叶子加点深度最小
3.叶子节点数最少且叶子节点深度最小。
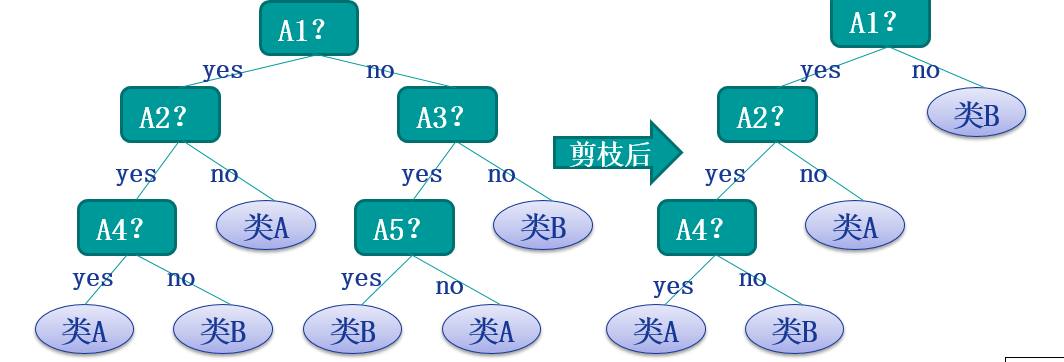
在实际的操作中还会设计到ID3算法的收敛,过度拟合等问题下面依次进行描述
1.ID算法收敛
2.过度拟合问题
1.ID3算法的收敛
当ID3确定根节点以及后续节点之后,因此当算法满足以下条件该分支的既可以结束
1.该群数据的每一个数据都已经归类到同一类别中
2.该群数据已经没有办法找到新的属性进行节点分割
3.该群数据已经没有任何尚未处理的数据。
2.过度拟合问题
原因:
造成多度拟合的潜在原因主要以下两个方面
1.噪声导致的过度拟合
比如错误的分类,或者属性值。
2.缺乏代表性样本所导致的过度拟合
方法:
1.预剪枝
通过提前停止树的构建而对树剪枝,一旦停止,节点就是树叶,该树叶持有子集元祖最频繁的类。
停止决策树生长最简单的方法有:
1.定义一个高度,当决策树达到该高度时就停止决策树的生长
2.达到某个节点的实例具有相同的特征向量,及时这些实例不属于同一类,也可以停止决策树的生长。这个方法对于处理
数据的数据冲突问题比较有效。
3.定义一个阈值,当达到某个节点的实例个数小于阈值时就可以停止决策树的生长
4.定义一个阈值,通过计算每次扩张对系统性能的增益,并比较增益值与该阈值大小来决定是否停止决策树的生长。
2.后剪枝方法
后剪枝(postpruning):它首先构造完整的决策树,允许树过度拟合训练数据,然后对那些置信度不够的结点子树用叶子结点来代替,该叶子的类标号用该结点子树中最频繁的类标记。相比于先剪枝,这种方法更常用,正是因为在先剪枝方法中精确地估计何时停止树增长很困难。
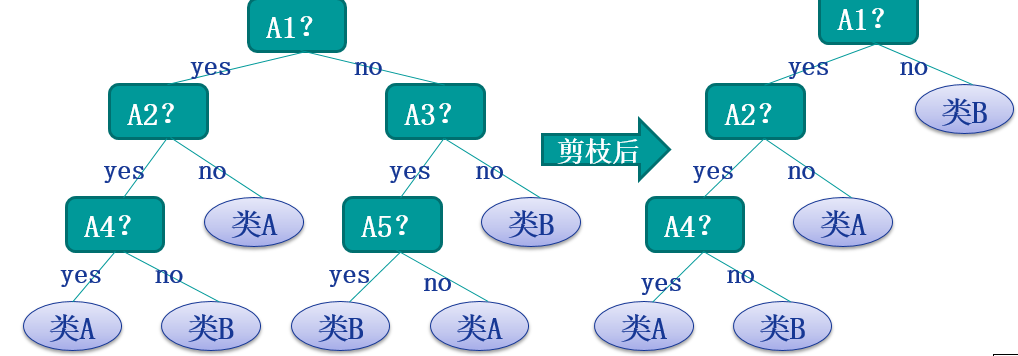
以上可以理解为后剪枝的基本思想,其中后剪枝方法主要有以下几个方法:
Reduced-Error Pruning(REP,错误率降低剪枝)
Pesimistic-Error Pruning(PEP,悲观错误剪枝)
Cost-Complexity Pruning(CCP,代价复杂度剪枝)
EBP(Error-Based
Pruning)(基于错误的剪枝)
以下分别进行说明:
1.REP
REP方法是一种比较简单的后剪枝的方法,在该方法中,可用的数据被分成两个样例集合:一个训练集用来形成学习到的决策树,一个分离的验证集用来评估这个决策树在后续数据上的精度,确切地说是用来评估修剪这个决策树的影响。
这个方法的动机是:即使学习器可能会被训练集中的随机错误和巧合规律所误导,但验证集合不大可能表现出同样的随机波动。所以验证集可以用来对过度拟合训练集中的虚假特征提供防护检验。
该剪枝方法考虑将书上的每个节点作为修剪的候选对象,决定是否修剪这个结点有如下步骤组成:
1:删除以此结点为根的子树
2:使其成为叶子结点
3:赋予该结点关联的训练数据的最常见分类
4:当修剪后的树对于验证集合的性能不会比原来的树差时,才真正删除该结点
因为训练集合的过拟合,使得验证集合数据能够对其进行修正,反复进行上面的操作,从底向上的处理结点,删除那些能够最大限度的提高验证集合的精度的结点,直到进一步修剪有害为止(有害是指修剪会减低验证集合的精度)。
REP是最简单的后剪枝方法之一,不过由于使用独立的测试集,原始决策树相比,修改后的决策树可能偏向于过度修剪。这是因为一些不会再测试集中出现的很稀少的训练集实例所对应的分枝在剪枝过如果训练集较小,通常不考虑采用REP算法。
尽管REP有这个缺点,不过REP仍然作为一种基准来评价其它剪枝算法的性能。它对于两阶段决策树学习方法的优点和缺点提供了了一个很好的学习思路。由于验证集合没有参与决策树的创建,所以用REP剪枝后的决策树对于测试样例的偏差要好很多,能够解决一定程度的过拟合问题。
2.PEP
悲观错误剪枝法是根据剪枝前后的错误率来判定子树的修剪。该方法引入了统计学上连续修正的概念弥补REP中的缺陷,在评价子树的训练错误公式中添加了一个常数,假定每个叶子结点都自动对实例的某个部分进行错误的分类。
把一颗子树(具有多个叶子节点)的分类用一个叶子节点来替代的话,在训练集上的误判率肯定是上升的,但是在新数据上不一定。于是我们需要把子树的误判计算加上一个经验性的惩罚因子。对于一颗叶子节点,它覆盖了N个样本,其中有E个错误,那么该叶子节点的错误率为(E+0.5)/N。这个0.5就是惩罚因子,那么一颗子树,它有L个叶子节点,那么该子树的误判率估计为:
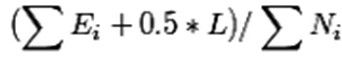
这样的话,我们可以看到一颗子树虽然具有多个子节点,但由于加上了惩罚因子,所以子树的误判率计算未必占到便宜。剪枝后内部节点变成了叶子节点,其误判个数J也需要加上一个惩罚因子,变成J+0.5。那么子树是否可以被剪枝就取决于剪枝后的错误J+0.5在的标准误差内。对于样本的误差率e,我们可以根据经验把它估计成各种各样的分布模型,比如是二项式分布,比如是正态分布。
那么一棵树错误分类一个样本值为1,正确分类一个样本值为0,该树错误分类的概率(误判率)为e(e为分布的固有属性,可以通过统计出来),那么树的误判次数就是伯努利分布,我们可以估计出该树的误判次数均值和标准差:
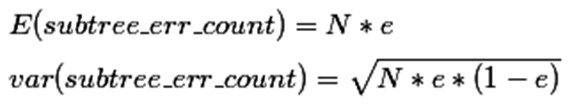
把子树替换成叶子节点后,该叶子的误判次数也是一个伯努利分布,其概率误判率e为(E+0.5)/N,因此叶子节点的误判次数均值为

使用训练数据,子树总是比替换为一个叶节点后产生的误差小,但是使用校正后有误差计算方法却并非如此,当子树的误判个数大过对应叶节点的误判个数一个标准差之后,就决定剪枝:

这个条件就是剪枝的标准。当然并不一定非要大一个标准差,可以给定任意的置信区间,我们设定一定的显著性因子,就可以估算出误判次数的上下界。
话不多说,上例子:
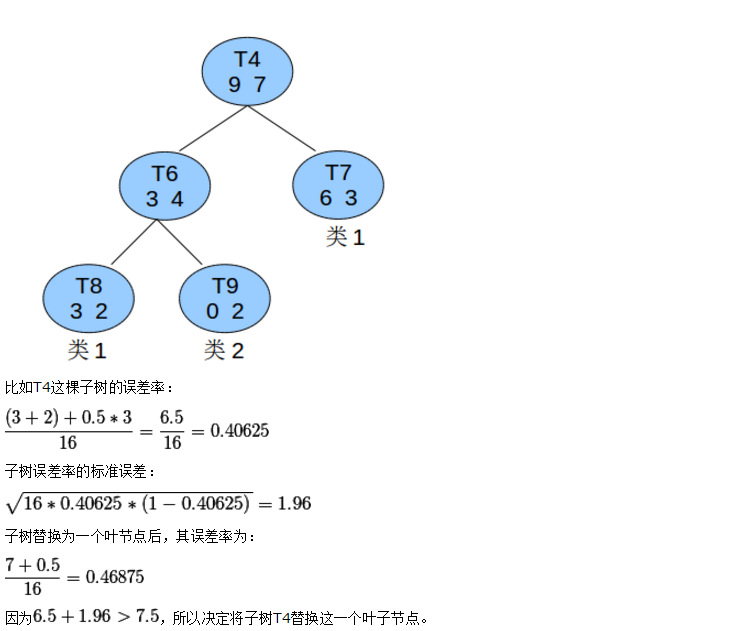
在上述例子中T8种的类1可以认为是识别错误的T4这课子树的估计错误为5,T4子树的最后叶子节点为3个
上述是悲观错误剪枝。
悲观剪枝的准确度比较高,但是依旧会存在以下的问题:
1.PeP算法实用的从从上而下的剪枝策略,这种剪枝会导致和预剪枝同样的问题,造成剪枝过度。
2.Pep剪枝会出现剪枝失败的情况。d
代价复杂度剪枝:
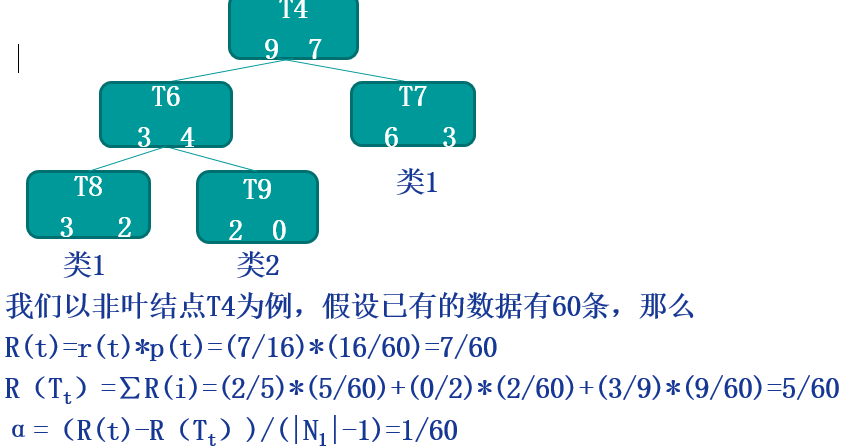
该算法为子树Tt定义了代价(cost)和复杂度(complexity),以及一个可由用户设置的衡量代价与复杂度之间关系的参数α,其中,代价指在剪枝过程中因子树Tt被叶节点替代而增加的错分样本,复杂度表示剪枝后子树Tt减少的叶结点数,α则表示剪枝后树的复杂度降低程度与代价间的关系,定义为:

其中,
|N1|:子树Tt中的叶节点数;
R(t):结点t的错误代价,计算公式为R(t)=r(t)*p(t),
r(t)为结点t的错分样本率,p(t)为落入结点t的样本占所有样本的比例;
R(Tt):子树Tt错误代价,计算公式为R(Tt)=∑R(i),i为子树Tt的叶节点。
CCP剪枝算法分为两个步骤:
1.对于完全决策树T的每个非叶结点计算α值,循环剪掉具有最小α值的子树,直到剩下根节点。在该步可得到一系列的剪枝树{T0,T1,T2......Tm},其中T0为原有的完全决策树,Tm为根结点,Ti+1为对Ti进行剪枝的结果;
2.从子树序列中,根据真实的误差估计选择最佳决策树。
上例子:
EBP:
以下是几种剪枝的方法的比较:
| REP | PEP | CCP | |
| 剪枝方式 | 自底向上 | 自顶向下 | 自底向上 |
| 计算复杂度 | 0(n) | o(n) | o(n2) |
| 误差估计 | 剪枝集上误差估计 | 使用连续纠正 | 标准误差 |