【Codeforces 335 E】—Counting Skyscrapers

传送门

当询问$Alice$的时候可以发现答案就是$n$
因为考虑如果跳过一个高度为$i$的
中间经过的楼房数量就是$2^i$
考虑枚举中间有几个房子等比数列算一下就可以得到了

考虑$Bob$时
考虑枚举高度$i$
即加入一个新的高度的绳子覆盖原来的
考虑枚举当前的长度$j$
那么可能在$n-j$个位置出现
概率是$(n-j)(1-frac{1}{2^i})^{j-1}*frac{1}{2^{2i}}$

考虑减去覆盖的上一个高度的期望（再之前的已经被减去了）
$i-1$的就是中间$j-1$个楼房中高度为$i-1$的个数的
个数就是$1+(j-1)*frac{1}{2^i-1}$

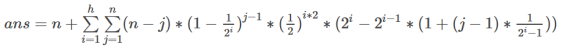
然后就完了

#include<bits/stdc++.h>
using namespace std;
const int RLEN=1<<20|1;
inline char gc(){
    static char ibuf[RLEN],*ib,*ob;
    (ob==ib)&&(ob=(ib=ibuf)+fread(ibuf,1,RLEN,stdin));
    return (ob==ib)?EOF:*ib++;
}
#define gc getchar
inline int read(){
    char ch=gc();
    int res=0,f=1;
    while(!isdigit(ch))f^=ch=='-',ch=gc();
    while(isdigit(ch))res=(res+(res<<2)<<1)+(ch^48),ch=gc();
    return f?res:-res;
}
#define ll long long
#define re register
#define pii pair<int,int>
#define fi first
#define se second
#define pb push_back
#define cs const
#define bg begin
template<class tp>inline void chemx(tp &a,tp b){a<b?a=b:0;}
template<class tp>inline void chemn(tp &a,tp b){a>b?a=b:0;}
int n,h;
double pw[73];
char s[10];
inline double ksm(double a,int b){
	double res=1;
	for(;b;b>>=1,a=a*a)if(b&1)res=res*a;
	return res;
}
int main(){
	scanf("%s",s+1);
	n=read(),h=read();
	if(s[1]=='A'){
		pw[0]=1;
		for(int i=1;i<=2*h;i++)pw[i]=pw[i-1]*0.5;
		double res=n;
		for(int i=1;i<=h;i++)
		for(int j=1;j<=n;j++)
		res+=1.0*(n-j)*ksm(1-pw[i],j-1)*pw[i*2]*((1<<i)-1.0*(1<<(i-1))*1.0*(1+1.0*(j-1)/((1<<i)-1)));
		printf("%.10f",res);
	}
	else cout<<n<<'
';
}