[敏捷软工个人项目博客]几何对象公共点

[个人项目作业] 平面图形的公共点个数

项目	内容
所属课程：北航-2020-春-软件工程	博客园班级博客链接
作业要求：计算平面图形的公共点个数	个人项目作业要求
我在这个课程的目标	提升在团队合作中开发“好软件”的能力
这个作业在哪些具体方面帮助我	根据《构建之法》前三章的内容搭建平面图形公共点个数计算程序，增加对个人开发流程的熟悉程度
教学班级	005
项目地址	https://github.com/Leomiku/ASE_personal_project.git

一、开始前PSP规划

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	30	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	120	120
· Design Spec	· 生成设计文档	120	30
· Design Review	· 设计复审 (和同事审核设计文档)	30	20
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	10	10
· Design	· 具体设计	180	60
· Coding	· 具体编码	600	240
· Code Review	· 代码复审	60	20
· Test	· 测试（自我测试，修改代码，提交修改）	180	60
Reporting	报告
· Test Report	· 测试报告	60	120
· Size Measurement	· 计算工作量	30	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	30
	合计	1480	730

二、解题思路描述

这道题的需求并不复杂，关键在于正确性和计算效率的要求。正确性可以用刚在《构建之法》中读到的单元测试加以保证，而计算效率则需要算法进行保证。

首先在抽象层面考虑问题，寻找高效率的解题算法。本题的基础问题为：计算平面中多条给定直线的公共点个数。首先映入脑海中的是复杂度为(O(n^2))的暴力算法。很自然就能想到可以利用平行关系和多条直线共点对暴力算法进行剪枝，却想不出降低算法阶数的办法。

用程序进行几何计算应该已经被前人探索过，互联网上应该存在相关资料。经过搜索后，题目的对应的领域浮出水面：计算几何，computational geometry。在几篇计算几何学相关的博客中，给出很多高效的几何计算方法：C++计算几何算法大全，但是这些方法对整体算法复杂度的降低并没有帮助。

一招不行，再出一招：从问题本身入手，用英语描述题目进行搜索。在WIKI百科中搜到了关于平面中直线相交的高效算法描述——Bentley–Ottmann algorithm，平均时间复杂度为(O((n+k)log{n})，其中n为直线数，k为交点数。在该WIKI百科中提到了当前的最优算法An optimal algorithm for finding segments intersections，其时间复杂度和空间复杂度达到了(O(nlog^2{n+k}))和(O(n))。

在准备好算法之后，可以进行项目方面的考量，好的算法固然高效，但也会拖慢项目的进度。考虑到笔者在写这段话时离作业截至只有两天，并且笔者还有其他两门作业，时间紧迫，所以首推使用(O(n^2))算法加剪枝的方法完成作业正确性的要求，若有时间，则尝试实现高效算法模块。

暴力算法的思路很自然：枚举所有直线的组合，遮掩自然能找出所有交点。

• 平行：在枚举遍历时，如果找到两条直线存在平行关系，则将两条直线加入同一平行直线集合中，并在之后的枚举中用平行直线集合进行加速。
• 多直线共点：在枚举遍历时，如果发现共点，则将当前枚举直线加入直线共点集合中，并在之后的枚举中用直线共点集合进行加速。

时间十分紧迫，以上优化方法没有实现。

直线之间交点计算

设两直线方程为

[A_1x+B_1y+C_1=0 \A_2x+B_2y+C_2=0 ]

联立解得，当(A_2B_1-A_1B_2 eq 0)时，有唯一交点坐标

[x = frac{B_2C_1 - C_2B_1}{A_2B_1-A_1B_2} \y = frac{A_1C_2 - A_2C_1}{A_2B_1-A_1B_2} ]

直线与圆之间的交点计算

设直线方程和圆方程分别为

[Ax+By+C=0 \(x-x_0)^2+(y-y_0)^2 = r^2 ]

首先根据圆心到直线距离与圆半径的关系判断直线与圆之间是否存在交点

如果存在交点，则将直线方程代入圆方程中，解得交点坐标

圆之间交点计算

联立圆方程进行求解较为困难，我们利用向量法求解圆之间交点。

参考博客为 计算几何学 | 圆与圆的交点 | Cross Points of Circles

（向量法实在是巧妙，我被向量法的魅力所折服。）

三、设计实现

自然的，本项目中会存在三个类：point, line, circle。

1. Point类

实现继承pair类

Point类的规格如下

字段	类型	属性/方法	解释
x	浮点型	属性	横坐标
y	浮点型	属性	纵坐标
==	bool	方法	判断两Point在平面上是否是同一点
hash<Point>	size_t	方法	提供Point对象的哈希值，针对浮点数特殊处理。

2. Line类

Line类的实现规格如下，使用一般式(Ax+By+C=0)表示直线

字段	类型	属性/方法	解释
A	浮点型	属性	x系数
B	浮点型	属性	y系数
C	浮点型	属性	常数

3. Circle类

circle类的实现规格如下，使用((x-x_0)^2 + (y-y_0)^2=r^2)的表示圆

字段	类型	属性/方法	解释
x_0	浮点型	属性	圆心横坐标
y_0	浮点型	属性	原型纵坐标
r	浮点型	属性	圆半径

4.IO类

IO类的功能如下

• 解析命令行参数，得到输入输出路径。
• 提供读取几何对象的接口。
• 提供输出结果的接口。

接口约定

接口功能	接口名	约定
读取几何对象的接口	read	返回装有输入文件所有行的vector<string>
输出几何对象的接口	write	输入为装有所有输出行的vector<string>

5.Canvas类

实现几何对象的管理和交互

字段	类型	属性/方法	解释
draw	int	方法	根据传入的字符串vector构建几何对象并计算其公共点
line_line_intersection	Point*	方法	计算传入的两条直线之间是否存在交点
line_circle_intersection	void	方法	计算传入的直线和圆之间是否存在交点
circle_circle_intersection	void	方法	计算传入的两个圆之间是否存在交点
intersect_points	unordered_set<Point>	属性	管理几何图形所形成的公共点

四、性能改进与分析

中等样本输入的性能查探器统计结果如下

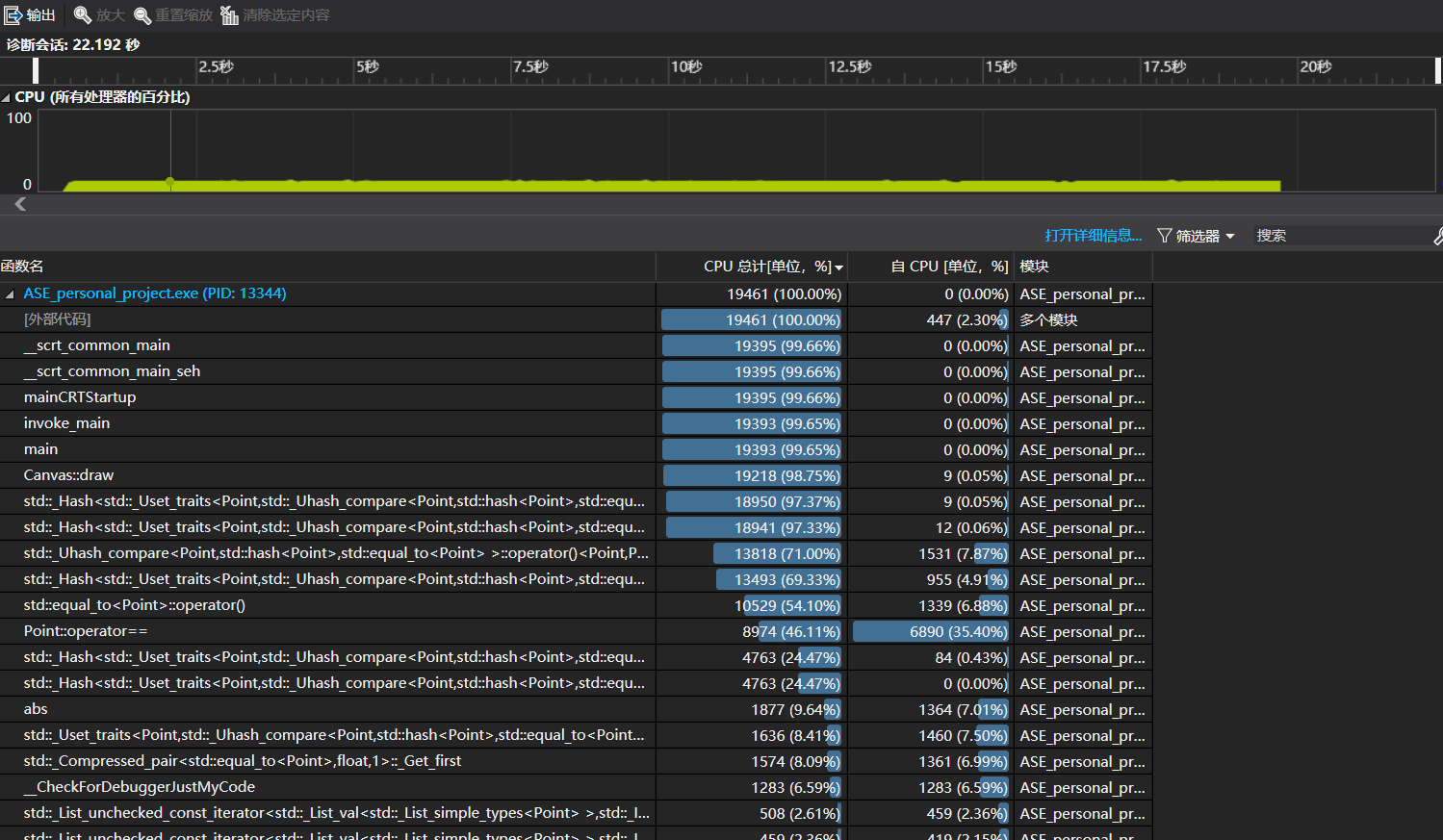
可以很明显的看出，在程序运行的过程中，hash函数占用了大量的时间。为此，我试验了用set替换unordered_set，性能表现并无明显变化。

五、代码说明

本题的关键为计算三种交点的计算方法

直线与直线之间的交点计算十分简单，直接套用公式就可以

inline Point* Canvas::line_line_intersection(Line* first, Line* second)
{
	double bottom = second->A * first->B - first->A * second->B;
	if (abs(bottom) < eps)
	{
		return NULL;
	}
	else
	{
		double x = (second->B * first->C - second->C * first->B) / bottom;
		double y = (first->A * second->C - second->A * first->C) / bottom;
		return new Point(x, y);
	}	
}

直线与圆之间交点的计算比较复杂，之所以代码这么长是因为考虑了圆与直线：{相切，相交} * {直线垂直于x轴，直线垂直于y轴，直线与两坐标轴都有交点} 6中情况。因为采用的方法是暴力联立再带入求根公式，所以表达式的来由并没什么要强调的。

Point* c1 = NULL, * c2 = NULL;
double d = abs(line->A * circle->x_0 + line->B * circle->y_0 + line->C) / sqrt(line->A * line->A + line->B * line->B);	// 计算圆心到直线的距离
if (fequal(d, circle->r))	// 直线与圆相切
{
double B;
double square_add = circle->x_0 * circle->x_0 + circle->y_0 * circle->y_0 - circle->r * circle->r;
double i_1_x, i_1_y, i_2_x, i_2_y;
if (line->A == 0)	// 直线垂直于y轴
{
B = -2 * circle->x_0;
i_1_x = -0.5 * B;
c1 = new Point(i_1_x, -line->C);
}
else if (line->B == 0)	//直线垂直于x轴
{
B = -2 * circle->y_0;
i_1_y = -0.5 * B;
c1 = new Point(-line->C, i_1_y);
}
else	// 直线与两个坐标轴都有交点
{
B = (2 * line->A * line->C - 2 * circle->x_0 - 2 * line->A * circle->y_0) / (line->A * line->A + 1);
i_1_x = -0.5 * B;
i_1_y = line->A * i_1_x + line->C;
c1 = new Point(i_1_x, i_1_y);
}
}
else if (d < circle->r) // 直线与圆有两个交点
{
double B, C, deta;
double square_add = circle->x_0 * circle->x_0 + circle->y_0 * circle->y_0 - circle->r * circle->r;
double i_1_x, i_1_y, i_2_x, i_2_y;
if (line->A == 0)	//直线垂直于y轴
{
B = -2 * circle->x_0;
C = square_add + 2 * line->C * circle->y_0 + line->C * line->C;
deta = sqrt(0.25 * B * B - C);
i_1_x = -0.5 * B + deta;
i_2_x = -0.5 * B - deta;
c1 = new Point(i_1_x, -line->C);
c2 = new Point(i_2_x, -line->C);
}
else if (line->B == 0)	//直线垂直于x轴
{
B = -2 * circle->y_0;
C = square_add + 2 * line->C * circle->x_0 + line->C * line->C;
deta = sqrt(0.25 * B * B - C);
i_1_y = -0.5 * B + deta;
i_2_y = -0.5 * B - deta;
c1 = new Point(-line->C, i_1_y);
c2 = new Point(-line->C, i_2_y);
}
else			//直线与两个坐标轴都有交点
{
B = (2 * line->A * line->C - 2 * circle->x_0 - 2 * line->A * circle->y_0) / (line->A * line->A + 1);
C = (square_add + line->C * line->C - 2 * line->C * circle->y_0) / (line->A * line->A + 1);
deta = sqrt(0.25 * B * B - C);
i_1_x = -0.5 * B + deta;
i_2_x = -0.5 * B - deta;
i_1_y = line->A * i_1_x + line->C;
i_2_y = line->A * i_2_x + line->C;
c1 = new Point(i_1_x, i_1_y);
c2 = new Point(i_2_x, i_2_y);
}
}

对于圆与圆之间的交点，采用向量法，较为简便

Point* ip_1 = NULL, * ip_2 = NULL;
double r_add = c_1->r + c_2->r, r_sub = abs(c_1->r - c_2->r); // 计算两圆半径之和与差
double c_dis = sqrt((c_1->x_0 - c_2->x_0) * (c_1->x_0 - c_2->x_0) + (c_1->y_0 - c_2->y_0) * (c_1->y_0 - c_2->y_0));				// 计算两圆圆心距离
if (fequal(r_add, c_dis))
{						// 若两圆外切，则直接计算加权平均
    ip_1 = new Point((c_1->x_0 * c_2->r + c_2->x_0 * c_1->r) / (c_1->r + c_2->r),
                     (c_1->y_0 * c_2->r + c_2->y_0 * c_1->r) / (c_1->r + c_2->r));
}
else if (fequal(r_sub, c_dis))
{					
// 若两圆内切，则先将圆心相减计算向量v，再按照大圆半径长与v模之比对v进行缩放，最后将缩放后的v与大圆圆心相加得切点。
    Circle *small, *large;
    if (c_1->r > c_2->r)
    {
        small = c_2;
        large = c_1;
    }
    else
    {
        small = c_1;
        large = c_2;
    }
    double c12_v_x = small->x_0 - large->x_0;
    double c12_v_y = small->y_0 - large->y_0;
    double riot = large->r / sqrt(c12_v_x * c12_v_x + c12_v_y * c12_v_y);
    ip_1 = new Point(large->x_0 + riot * c12_v_x, large->y_0 + riot * c12_v_y);
}
else if (c_dis > r_sub && c_dis < r_add)
{
// 若两圆存在两个交点，则先利用余弦定理计算出某一个交点与大圆连线和两圆圆心连线之间的夹角。再计算出两圆圆心之间的夹角。通过正余弦和差角公式计算出大圆与交点连线与x轴的夹角。最后辅以大圆半径长及大圆圆心坐标就能计算出交点坐标。
    double c12_v_x = c_2->x_0 - c_1->x_0;
    double c12_v_y = c_2->y_0 - c_1->y_0;
    double cos_ceta = (c_1->r * c_1->r + c_dis * c_dis - c_2->r * c_2->r) / (2 * c_1->r * c_dis);
    double sin_ceta = sqrt(1 - cos_ceta * cos_ceta);
    double sin_alpa = c12_v_y / sqrt(c12_v_x * c12_v_x + c12_v_y * c12_v_y);
    double cos_alpa = c12_v_x / sqrt(c12_v_x * c12_v_x + c12_v_y * c12_v_y);
    double sin_1 = sin_alpa * cos_ceta + cos_alpa * sin_ceta;
    double cos_1 = cos_alpa * cos_ceta - sin_alpa * sin_ceta;
    double sin_2 = sin_alpa * cos_ceta - cos_alpa * sin_ceta;
    double cos_2 = cos_alpa * cos_ceta + sin_alpa * sin_ceta;
    ip_1 = new Point(c_1->x_0 + c_1->r * cos_1, c_1->y_0 + c_1->r * sin_1);
    ip_2 = new Point(c_1->x_0 + c_1->r * cos_2, c_1->y_0 + c_2->r * sin_2);
}

六、单元测试与代码检查

1.代码检查

通过Code Quality Analyze，已无警告存在

2.单元测试

单元测试运行结果如下