转自:http://www.cnblogs.com/jillzhang/archive/2006/11/02/547679.html
哈希表和哈希函数是大学数据结构中的课程,实际开发中我们经常用到Hashtable这种结构,当遇到键-值对存储,采用Hashtable比ArrayList查找的性能高。为什么呢?我们在享受高性能的同时,需要付出什么代价(这几天看红顶商人胡雪岩,经典台词:在你享受这之前,必须受别人吃不了的苦,忍受别人受不了的屈辱),那么使用Hashtable是否就是一桩无本万利的买卖呢?就此疑问,做以下分析,希望能抛砖引玉。
1)hash它为什么对于键-值查找性能高
学过数据结构的,都应该晓得,线性表和树中,记录在结构中的相对位置是随机的,记录和关键字之间不存在明确的关系,因此在查找记录的时候,需要进行一系列的关键字比较,这种查找方式建立在比较的基础之上,在.net中(Array,ArrayList,List)这些集合结构采用了上面的存储方式。
比如,现在我们有一个班同学的数据,包括姓名,性别,年龄,学号等。假如数据有
| 姓名 | 性别 | 年龄 | 学号 |
| 张三 | 男 | 15 | 1 |
| 李四 | 女 | 14 | 2 |
| 王五 | 男 | 14 | 3 |
假如,我们按照姓名来查找,假设查找函数FindByName(string name);
1)查找“张三”
只需在第一行匹配一次。
2)查找"王五"
在第一行匹配,失败,
在第二行匹配,失败,
在第三行匹配,成功
上面两种情况,分别分析了最好的情况,和最坏的情况,那么平均查找次数应该为 (1+3)/2=2次,即平均查找次数为(记录总数+1)的1/2。
尽管有一些优化的算法,可以使查找排序效率增高,但是复杂度会保持在log2n的范围之内。
如何更更快的进行查找呢?我们所期望的效果是一下子就定位到要找记录的位置之上,这时候时间复杂度为1,查找最快。如果我们事先为每条记录编一个序号,然后让他们按号入位,我们又知道按照什么规则对这些记录进行编号的话,如果我们再次查找某个记录的时候,只需要先通过规则计算出该记录的编号,然后根据编号,在记录的线性队列中,就可以轻易的找到记录了 。
注意,上述的描述包含了两个概念,一个是用于对学生进行编号的规则,在数据结构中,称之为哈希函数,另外一个是按照规则为学生排列的顺序结构,称之为哈希表。
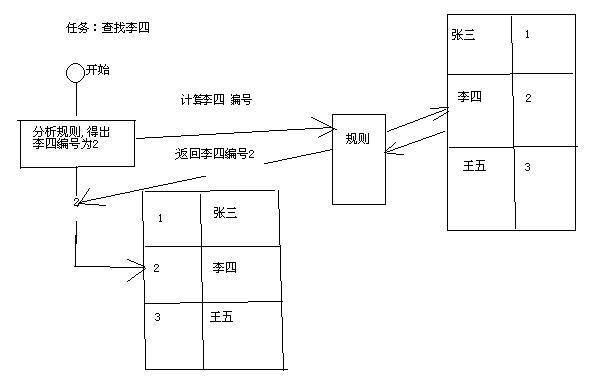
仍以上面的学生为例,假设学号就是规则,老师手上有一个规则表,在排座位的时候也按照这个规则来排序,查找李四,首先该教师会根据规则判断出,李四的编号为2,就是在座位中的2号位置,直接走过去,“李四,哈哈,你小子,就是在这!”
看看大体流程:
从上面的图中,可以看出哈希表可以描述为两个筒子,一个筒子用来装记录的位置编号,另外一个筒子用来装记录,另外存在一套规则,用来表述记录与编号之间的联系。这个规则通常是如何制定的呢?
a)直接定址法:
我在前一篇文章对GetHashCode()性能比较的问题中谈到,对于整形的数据GetHashCode()函数返回的就是整形 本身,其实就是基于直接定址的方法,比如有一组0-100的数据,用来表示人的年龄
那么,采用直接定址的方法构成的哈希表为:
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0岁 | 1岁 | 2岁 | 3岁 | 4岁 | 5岁 |
.....
这样的一种定址方式,简单方便,适用于元数据能够用数字表述或者原数据具有鲜明顺序关系的情形。
b)数字分析法:
有这样一组数据,用于表述一些人的出生日期
| 年 | 月 | 日 |
| 75 | 10 | 1 |
| 75 | 12 | 10 |
| 75 | 02 | 14 |
分析一下,年和月的第一位数字基本相同,造成冲突的几率非常大,而后面三位差别比较大,所以采用后三位
c)平方取中法
取关键字平方后的中间几位作为哈希地址
d) 折叠法:
将关键字分割成位数相同的几部分,最后一部分位数可以不相同,然后去这几部分的叠加和(取出进位)作为哈希地址,比如有这样的数据20-1445-4547-3
可以
5473
+ 4454
+ 201
= 10128
取出进位1,取0128为哈希地址
e)取余法
取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。H(key)=key MOD p (p<=m)
f) 随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key)=random(key) ,其中random为随机函数。通常用于关键字长度不等时采用此法。
总之,哈希函数的规则是:通过某种转换关系,使关键字适度的分散到指定大小的的顺序结构中。越分散,则以后查找的时间复杂度越小,空间复杂度越高。
2)使用hash,我们付出了什么?
hash是一种典型以空间换时间的算法,比如原来一个长度为100的数组,对其查找,只需要遍历且匹配相应记录即可,从空间复杂度上来看,假如数组存储的是byte类型数据,那么该数组占用100byte空间。现在我们采用hash算法,我们前面说的hash必须有一个规则,约束键与存储位置的关系,那么就需要一个固定长度的hash表,此时,仍然是100byte的数组,假设我们需要的100byte用来记录键与位置的关系,那么总的空间为200byte,而且用于记录规则的表大小会根据规则,大小可能是不定的,比如在lzw算法中,如果一个很长的用于记录像素的byte数组,用来记录位置与键关系的表空间,算法推荐为一个12bit能表述的整数大小,那么足够长的像素数组,如何分散到这样定长的表中呢,lzw算法采用的是可变长编码,具体会在深入介绍lzw算法的时候介绍。
注:hash表最突出的问题在于冲突,就是两个键值经过哈希函数计算出来的索引位置很可能相同。