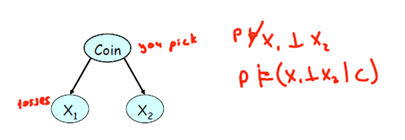
之后要用到的定义
Factor 是定义在一系列variables上的函数。它的定义域就是这些variable构成的笛卡尔积。
引入factor的原因
1 Fundamental building block for defining distributions in high-dimensional spaces
2 Set of basic operations for manipulating these probability distributions
在此基础上,我们定义factor的一系列操作
1 product
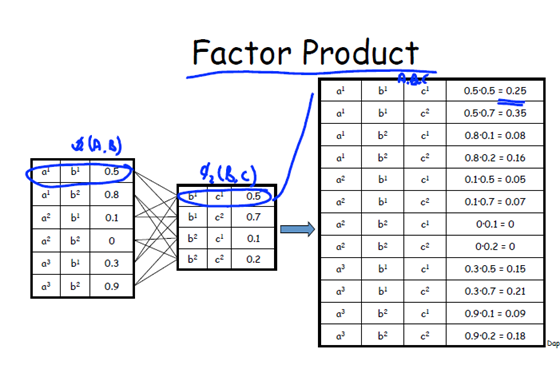
2Factor Marginalization
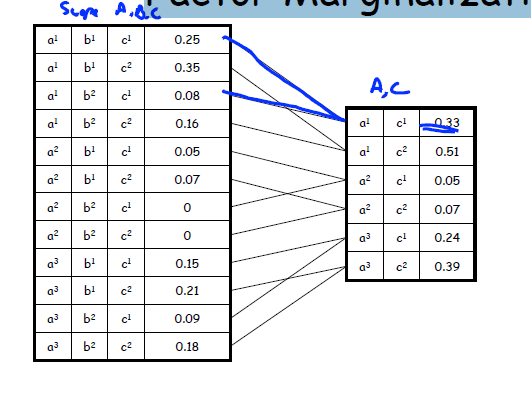
注意:Factor production 与我们概率意义上的合并有不同。
Week 1 主要是介绍贝叶斯网络的基本定义和结构。并将他和严密的概率论中的"独立性"关联起来。
一、Defination
(1)结构上:有向图
(2)数值上:For each node Xi a CPD P(Xi | ParG(Xi))
这两点其实能描述一个bayesian network 的全部性质。
Bayesian network 其实表达的东西是 Joint Distribution over the nodes(variables) and this Joint distribution is defined by the
(1)Structure of the networks(who is the parents and who is the children)
(2)The chain rule P(X1,…,Xn) = Πi P(Xi | ParG(Xi)).
注意:
站在纯数学(数值)层面上来看,Bayesian network做的就是这么一件事:在一个有向图上定义一个量。这个量的定义为:P(X1,…,Xn) = Πi P(Xi | ParG(Xi)). 更准确的说是定义一种函数/factor,函数的定义域/scope 是variable的笛卡尔积。 也就是说到现在在为止,我们还没有将这种纯数学上的定义和概率论东西结合起来。然而,我们采用这种有向图的结构很显然暗示着这一烈的变量之间存在着依赖关系,采用一个"图"的模型就是为了方便的刻画这种依赖关系。
接下来一部分就是在做这样一件事情,将图的结构和概率论上的"独立"联系起来。
二、图的结构和变量间的依赖关系
1、一个例子
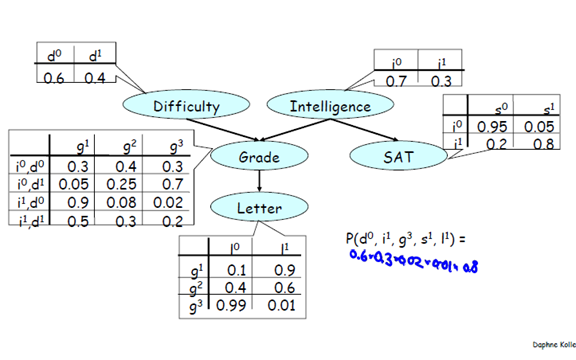
2 关于这个例子的一些讨论
我们究竟要干嘛呢。什么叫建立图的结构和变量间依赖关系呢。看到这张图。我们很明显地希望/认为
(1)对Difficulty 和 Intelligence 的观测是会影响 Letter 的概率分布的。而且是很明显的通过影响Grade 影响 Letter。
解释:在这里,所谓的"影响"讲的很抽象,到底什么是影响,为什么会影响。要说明白这一点还要提到,bayesian network的原理。之前我们已经讲到了贝叶斯网络的定义,一种第一在variable的笛卡尔积上的函数,我们可以认为一旦这个函数定义好了之后,这个贝叶斯网络模型就是静态的了。我们输入自变量,variables的一种排列,就能得到一个对应的值/概率。
然而,这其实并不是我们想要的,我们往往感兴趣的并不是针对"全部变量"计算出来的概率。实际问题的结构往往是:
(1)我们有部分变量的观测值
(2)我们关心的往往仅仅是其中的一个变量。
所以,我们要做的就是根据观测值,得到关于某一个变量的概率分布。
比如,Difficulty:难。Intelligence:中等。SAT:高分。预测能否那道Letter.
解决这个问题只要做两件事情:
(1)修改Difficulty,Intelligence 的概率分布。Difficulty:难的概率改为:1. …
(2)根据新的图,计算factors over the graph,之后在做关于variable Letter的一个factor Marginalization
我们很可能甘短困惑,why bother! 这几根据最后一节点不就好了么,然而这不是计算机处理的方式,也不是一个general solution.我们这种方法能处理一般性的问题。所有的这类为题都可以这样来做:
(1)根据obsered evidence,修改某些factor
(2)计算Joint Distribution
(3) 在Joint Distribution 的基础上做关于我们想要变量的marginalization.
这里需要注意的是Joint Distribution 和单纯的将各个factors 做production 有所不同。Joint Distribution 还应该多有一个normalization的过程。即概率的归一化。
3 将图的结构和概率意义上各个变量间的依赖关系建立起来。
3.1
先建立描述图的结构的语言: Active trail 和描述变量间的依赖关系的概率论上的概念:独立和条件独立
A trail X1 ─ … ─ Xn is active given Z if:
– for any v-structure Xi-1 → Xi ← Xi+1 we have that Xi or one of its descendants ∈Z
– no other Xi is in Z

独立:

条件独立

硬币:0.5、0.5 和biased,0.7,0.3
3.2 Factorization 和 Independecy 的联系
Factorization of a distribution P implies independencies that hold in P
If P factorizes over G, can we read these independencies from the structure of G?
结论:
就是在数学上的factorization和概率上的dependence上建立一种联系。
从最简单的独立性出发,根据chain rule ,很好就证明了。