欧拉定理，欧拉降幂

在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质定理。了解欧拉定理之前先来看一下费马小定理：

a是不能被质数p整除的正整数，则有a^(p-1) ≡ 1 (mod p)

欧拉给出了推广形式

若n，a为正整数且互质，则，其中φ(n)表示小于等于n的数中与n互质的数的数目。可以看出费马小定理是欧拉定理的一种特殊情况。

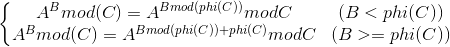
证明（好文章）：https://zhuanlan.zhihu.com/p/24902174

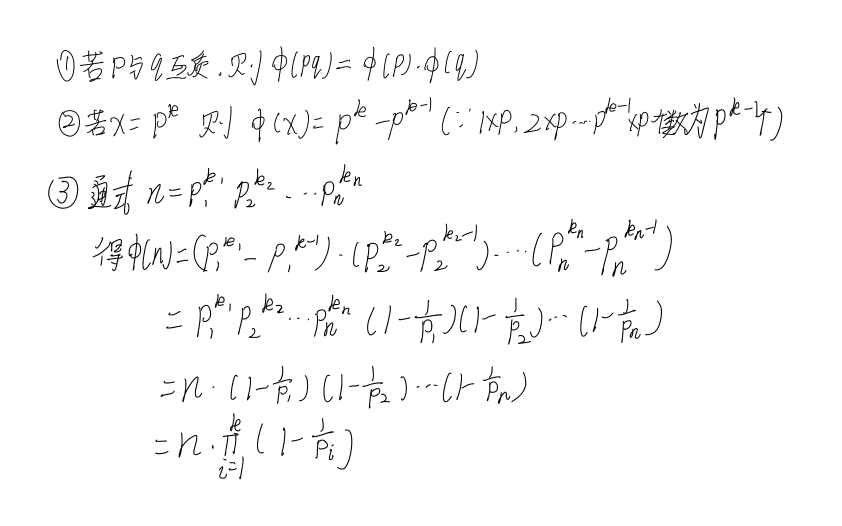
欧拉函数板子：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 1e6+5;
LL n;
LL get_Euler(LL x)
{
    LL res = x; ///初始值
    for(LL i = 2LL; i * i <= x; ++i) 
    {
        if(x % i == 0) 
        {
            res = res / i * (i - 1); ///先除后乘，避免数据过大
            while(x % i == 0) 
                x /= i;
        }
    }
    if(x > 1LL) 
        res = res / x * (x - 1); ///若x大于1，则剩下的x必为素因子
    return res;
}

int main(){
    while(cin >> n) {
        cout << get_Euler(n) << endl; ///求n的互质数的个数
       // cout << n * get_Euler(n) / 2 << endl; ///求n的所有互质数之和
    }
    return 0;
} 
//预处理打表写法：
/* 
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <vector>
#include <set>
using namespace std;
typedef long long LL;
const int maxn = 1e6+5;
int n, phi[maxn];
void phi_table() {
    phi[0] = 0, phi[1] = 1; ///1的欧拉函数值为1，唯一与1互质的数
    for(int i = 2; i < maxn; ++i) phi[i] = i; //先初始化为其本身
    for(int i = 2; i < maxn; ++i) {
        if(phi[i] == i) { ///如果欧拉函数值仍为其本身，说明i为素数
            for(int j = i; j < maxn; j += i) ///把i的欧拉函数值改变，同时也把能被素因子i整除的数的欧拉函数值改变
                phi[j] = phi[j] / i * (i - 1);
        }
    }
}
int main(){
    phi_table(); 
    int m;
    while(cin >> n>>m) {
        int sum=0;
        //cout << phi[n] << endl;
        for(int i=n;i<=m;i++)
            sum+=phi[i];
        cout<<sum<<endl;
    }
    return 0;
} */ 

题：https://vjudge.net/problem/FZU-1759

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int M=1e6+6;
char s[M];
typedef long long ll;
ll ph(ll x)
{
    ll res = x; ///初始值
    for(ll i = 2LL; i * i <= x; ++i) 
    {
        if(x % i == 0) 
        {
            res = res / i * (i - 1); ///先除后乘，避免数据过大
            while(x % i == 0) 
                x /= i;
        }
    }
    if(x > 1ll) 
        res = res / x * (x - 1); ///若x大于1，则剩下的x必为素因子
    return res;
}
ll ksm(ll a,ll b,ll mod){
    ll t=1;
    while(b){
        if(b&1)
            t=(t*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return t;
}
int main(){
    ll a,m;
    while(~scanf("%I64d %s %I64d",&a,s,&m)){
        ll ans=0;
        int len=strlen(s);
        ll p=ph(m);
        
        for(int i=0;i<len;i++)
            ans=(ans*10+s[i]-'0')%p;
        //cout<<p<<endl;
        ans+=p;
        printf("%I64d
",ksm(a,ans,m));
    }
    return 0;
}

经典题：https://www.lydsy.com/JudgeOnline/problem.php?id=3884

指数是无穷的，但是模数是有限的，从不断减小p去考虑。

因为次数是无穷的，所以B肯定>=ph()，所以采用第二条式子去递归

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long ll;
ll ph(ll x){
    ll ans=x;
    for(ll i=2ll;i*i<=x;i++){
        if(x%i==0){
            ans=ans/i*(i-1);
            while(x%i==0)
                x/=i;
        }
    }
    if(x>1ll)
        ans=ans/x*(x-1);
    return ans;
}
ll ksm(ll a,ll b,ll mod){
    ll t=1;
    while(b){
        if(b&1)
            t=(t*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return t;
}
ll dfs(ll p){
    if(p==1)
        return 0;
    ll k=ph(p);
    return ksm(2,dfs(k)+k,p);
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        ll p;
        scanf("%lld",&p);
        printf("%lld
",dfs(p));
    }
    return 0;
}