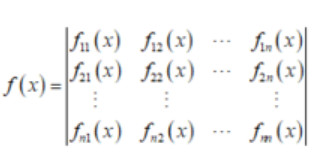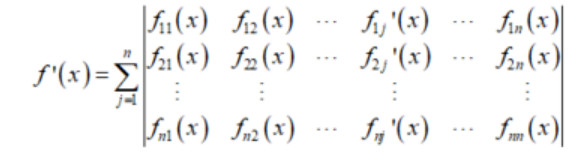2020 CCPC Wannafly Winter Camp Day1 Div.1&2 D 生成树 基尔霍夫矩阵带权版，线性代数求导

题：https://ac.nowcoder.com/acm/contest/3979/D

题意：题意是：有n个点，有2个边集构成了2个图G1，G2。要求在G1中的每个生成树有多少条边同时在G2中存在 

分析：基尔霍夫矩阵带权值版本，在g1中权值为0，同时在g1，g2中权值为1，（因为0为没价值，所以我们用1代表0，x代表1），求生成树的权值和；

　　　得到的基尔霍夫矩阵主子式行列式为f（x）=∑a_i *xⁱ 这里的a_i代表权值为权值为 i 的生成树的方案数，所以答案：Σi*a_i 即等价于f ' (1)；

　　　求导过程如图：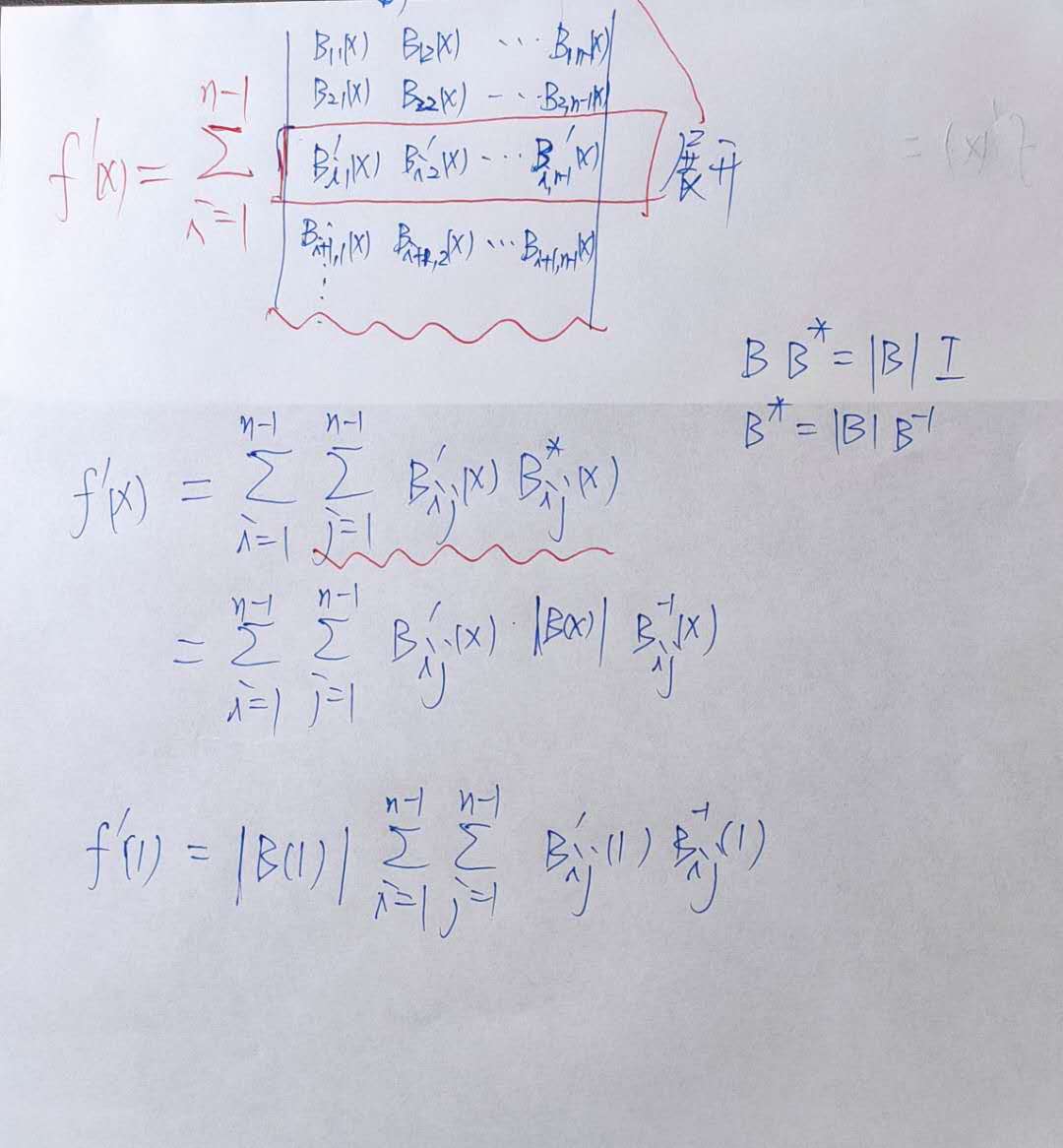

　　　所以只要求|B（1）| 以及B' 和B的逆矩阵；

　　　其中B‘ 即为代码中的g2，因为B的每个位置只会有1个x；|B（1）|为D；B^-1为inv；

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
const int inf=0x3f3f3f3f;
const ll INF=1e18;
const int M=404;
const int mod=998244353;
ll g1[M][M],g2[M][M],x[M];
char s[M];
ll ksm(ll x,ll y){
    ll t=1;
    while(y){
        if(y&1)
            t=(t*x)%mod;
        x=(x*x)%mod;
        y>>=1;
    }
    return t;
}
ll A[M][M];
ll Det(int n){///求行列式
    ll res=1;
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j++){
            if(A[j][i]!=0){
                swap(A[i],A[j]);
                if(i!=j)
                    res*=-1;
                break;
            }
        }
        for(int j=i+1;j<=n;j++){
            ll c=A[j][i]*ksm(A[i][i],mod-2)%mod;
            for(int k=i;k<=n;k++)
                (A[j][k]-=c*A[i][k])%=mod;
        }
    }
    for(int i=1;i<=n;i++) (res*=A[i][i])%=mod;
    res=(res+mod)%mod;
    return res;
}
ll G[M][M],inv[M][M];
///利用将G转化为单位矩阵进而将单位矩阵inv转化为G的逆矩阵
void Gauss(int n){
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j++){
            if(G[j][i]!=0){
                swap(G[i],G[j]);
                swap(inv[i],inv[j]);
                break;
            }
        }
        ll c=ksm(G[i][i],mod-2);
        for(int j=1;j<=n;j++)
            (G[i][j]*=c)%=mod,(inv[i][j]*=c)%=mod;
        ///将同列消成0
        for(int j=1;j<=n;j++){
            if(i!=j){
                c=G[j][i];
                for(int k=1;k<=n;k++){
                    (G[j][k]-=c*G[i][k])%=mod;
                    (inv[j][k]-=c*inv[i][k])%=mod;
                }

            }
        }
    }
}
void Inv(int n){
    for(int i=1;i<=n;i++){
        inv[i][i]=1;
        for(int j=1;j<=n;j++)
            G[i][j]=A[i][j];
    }
    Gauss(n);
}
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        for(int j=1;j<=n;j++){
            g1[i][j]=s[j]-'0';
            if(i<j&&g1[i][j]){
                A[i][i]++,A[j][j]++;
                A[i][j]--,A[j][i]--;
            }
        }
    }
    for(int i=1;i<=n;i++){
        scanf("%s",s+1);
        for(int j=1;j<=n;j++){
            g2[i][j]-=g1[i][j]&(s[j]-'0');
            if(i!=j)
                g2[i][i]-=g2[i][j];
        }
    }
    Inv(n-1);
    ll D=Det(n-1);
    ll ans=0;
    for(int i=1;i<=n-1;i++)
        for(int j=1;j<=n-1;j++){
            ans=(ans+inv[i][j]*D%mod*g2[i][j]%mod+mod)%mod;
        }
    printf("%lld
",ans);
    return 0;
}

矩阵求导法则：