E. Bricks（最少1*x 覆盖矩阵，最大独立集）

题：https://codeforces.com/contest/1404/problem/E

题意：给定n*m矩阵‘#’表示要用砖头覆盖，‘.’表示不能被覆盖，只有1*x的砖头（x可任意），问在砖头不相互覆盖的前提下，最少用几块砖头能按规定把矩阵覆盖

分析：

• 假设一开始全部都是1*1的砖头去覆盖，那么就有sum块（‘#’点的个数），要是相邻边合并sum减1，那么就是求在合法情况下最多能合并多少边；
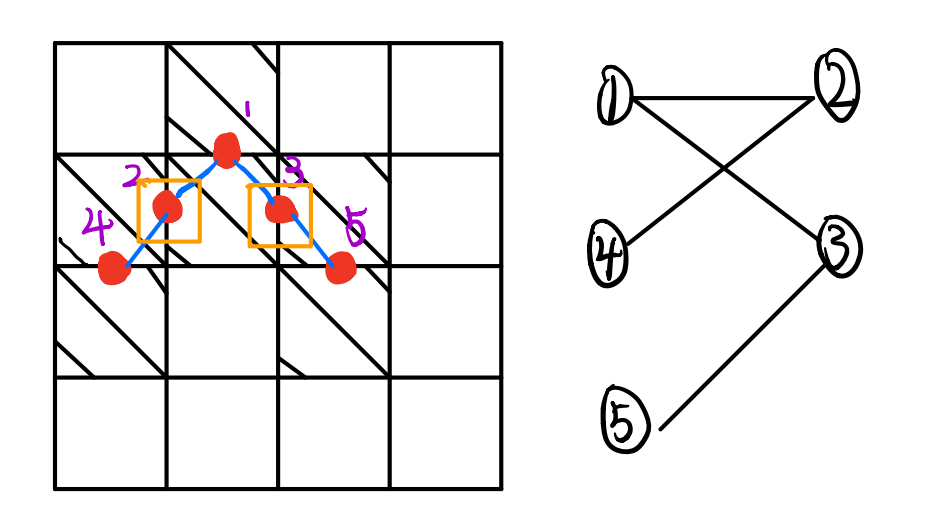
• 在合法情况下就是限制的1*x，也就不能出现‘L’型砖头，假设要是俩块砖头能形成‘L’型，那么就将这俩块砖头连边(以对偶图的形式)（这明显就是一个二分图的模型）；
• 合法情况就是求独立集（点集中各点没有连边）大小；
• 而最大独立集就是二分图中节点-最小点覆盖，应用到这道题上就是去掉这些点，相应连的边也就没有了，相当于花了贡献把这些点独立出来，剩下的点也就相互独立了；
• ans=sum-最大独立集。
• (下图标号只是方便，不代表该点的真实点标号)

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define pb push_back
const int inf=0x3f3f3f3f;
const ll INF=(1ll<<40);
const int M=1e6+5;
const int N=250;
int tot,S,T,n,m;
struct node{
    int u,v,nextt;
    int w;
}e[M<<1];
char s[N][N];
int head[M],deep[M],cur[M];
void addedge(int u,int v,int w){
    e[tot].v=v;
    e[tot].w=w;
    e[tot].nextt=head[u];
    head[u]=tot++;
    e[tot].v=u;
    e[tot].w=0;
    e[tot].nextt=head[v];
    head[v]=tot++;
}
bool bfs(){
    for(int i=0;i<=T;i++)
        deep[i]=0;
    queue<int>que;
    que.push(S);
    deep[S]=1;
    while(!que.empty()){
        int u=que.front();
        que.pop();
        for(int i=head[u];~i;i=e[i].nextt){
            int v=e[i].v;
            if(e[i].w>0&&deep[v]==0){
                deep[v]=deep[u]+1;
                if(v==T)
                    return true;
                que.push(v);
            }
        }
    }
    return deep[T]!=0;
}
int dfs(int u,int fl){

    if(u==T)
        return fl;
    int ans=0,x=0;
    for(int i=cur[u];~i;i=e[i].nextt){
        int v=e[i].v;
        if(e[i].w>0&&deep[v]==deep[u]+1){
            x=dfs(v,min(fl-ans,e[i].w));
            e[i].w-=x;
            e[i^1].w+=x;
            ans+=x;
            if(ans==fl)
                return ans;
            if(e[i].w)
                cur[u]=i;

        }
    }
    if(ans==0)
        deep[u]=0;
    return ans;
}
int dinic(){
    int res=0;
    while(bfs()){
        for(int i=0;i<=T;i++)
            cur[i]=head[i];
        res+=dfs(S,inf);
    }
    return res;
}
int getid(int x,int y,int other){
    return (x-1)*m+y+other;
}
int main(){

    scanf("%d%d",&n,&m);

    S=2*n*m+10,T=S+1;
    for(int i=0;i<=T;i++)
        head[i]=-1;
    for(int i=1;i<=n;i++)
        scanf("%s",s[i]+1);

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++)
            if(s[i][j]=='#'){
                ///将横纵作为二分图的两边
                ///L R在对偶图上相差1
                int L = (j-1>=1&&s[i][j-1]=='#') ? getid(i,j-1,0) : 0;
                int R = (j+1<=m&&s[i][j+1]=='#') ? getid(i,j-1,1) : 0;
                ///U D在对偶图上相差m
                int U = (i-1>=1&&s[i-1][j]=='#') ? getid(i-1,j,n*m) : 0;
                int D = (i+1<=n&&s[i+1][j]=='#') ? getid(i-1,j,n*m+m) : 0;
                if(L&&U) addedge(L,U,1);
                if(L&&D) addedge(L,D,1);
                if(R&&U) addedge(R,U,1);
                if(R&&D) addedge(R,D,1);
            }
    }
    int sum=0;
    int res=0;///二分图点数
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            if(s[i][j]=='#'){
                sum++;
                ///row点连接S
                if(j+1<=m&&s[i][j+1]=='#')
                    addedge(S,getid(i,j-1,1),1),res++;
                ///colu点连接T
                if(i+1<=n&&s[i+1][j]=='#')
                    addedge(getid(i-1,j,n*m+m),T,1),res++;
            }

    printf("%d
",sum-(res-dinic()));
    return 0;
}