【字符串】Manacher

【 快速寻找出一字符串内的最长回文子串 】

以abaaba为例

 

因为回文串也分为奇数长度与偶数长度的

所以回文子串的中心点可能是某个字符，也可能是某两个字符之间

所以算法先会预处理初始字符串，让每两个字符之间加一个原本不存在的特殊字符

 

即原串会先被处理为 #a#b#a#a#b#a#

然后为了防止数组越界，在左右两边再添加不同的特殊字符

左边加个@，右边直接 结束符

所以可见串会被处理成 @#a#b#a#a#b#a#

 

该部分代码为：

void initStr(){//重定义字符串
    int k=0;
    str[k++]='@';//开头加个特殊字符防止越界
    for(int i=0;i<len;i++){
        str[k++]='#';
        str[k++]=s[i];
    }
    str[k++]='#';
    len=k;
    str[k]='';//字符串尾设置为，防止越界
}

//好处就是如果回文串长度为奇数，中心就是原本的字符串中的字符

//如果长度是偶数，中心就是#号

 

然后定义三个变量和一个数组

mx 变量存目前处理到的所有回文串中，能到达的最右端的那个位置

id 变量存取到mx变量的那个回文串的中心字符

maxx，存回文串半径最大值，即答案 +1

数组 Len，Len[i] 表示以 i 这个位置为中心的最长回文串的半径

 

首先还是让i从0到len-1循环

上述三变量一数组全部置零

①    如果此时的i变量值小于mx，即目前i还是在前面处理到的最右端的那个回文串之内

　　那么就能靠回文串对称的关系，直接把可能的最小长度赋值给Len[i]

　　又因为id是取到mx的那个回文串的中心位置

　　所以我们可以拿i关于id对称的那个位置j，把Len[j]直接赋值给Len[i]先

　　j=id*2-i

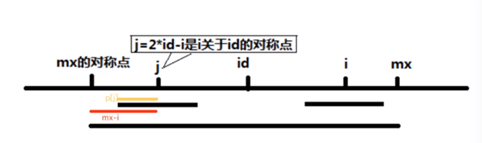
（图片来源 Bilibili av44612474）

　　因为i之前的所有位置的Len都是已经求出来的

　　所以直接拿对称点j，j能对称的长度可以先拿来给i

　　但又因为可能Len[j]的左端在mx对称点左侧

　　所以此时我们的Len[i]的右端又不能超过mx，即Len[i]=min(mx-i,Len[j])

②    如果此时的i变量值大于等于mx，直接赋值1先，因为单个字符肯定也是回文串

　　该部分代码为：

if(mx>i)
    Len[i]=min(mx-i,Len[2*id-i]);
else
    Len[i]=1;

　　初始赋值完成后开始向两边搜索能不能使这个回文串变更长

　　即已知i和此时的Len[i]，开始向两边推

　　代码为：

while(str[i+Len[i]]==str[i-Len[i]])
    Len[i]++;

　　最后，看看能不能更新三变量即可

if(Len[i]+i>mx){ 
    mx=Len[i]+i;
    id=i;
    maxx=max(maxx,Len[i]);
}

例题 HDU3068

总代码如下：

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+5;
char s[MAXN],str[MAXN*2];
int Len[MAXN*2],len=0;
/*
    Len[i]表示以i为中心点的最长的回文串的半径，包括i位置本身
*/
void initStr(){//重定义字符串
    int k=0;
    str[k++]='@';//开头加个特殊字符防止越界
    for(int i=0;i<len;i++){
        str[k++]='#';
        str[k++]=s[i];
    }
    str[k++]='#';
    len=k;
    str[k]='';//字符串尾设置为，防止越界
}
int manacher(){
    int mx=0,id=0,maxx=0;
    /*
        mx为当前处理到的回文串到达的最右边位置
        id为当前处理到的到达mx位置的回文串的中心点
        maxx为最长的Len，减去1后即为答案
    */
    for (int i=1;i<len;i++){
        if(mx>i)
            Len[i]=min(mx-i,Len[2*id-i]);//判断当前的点是否超过mx，没超过则可以通过取i关于id的对称点（已经求出来的）的Len值作为初始值
        else
            Len[i]=1;//如果超过了mx，初始值就等于1
        while(str[i+Len[i]]==str[i-Len[i]])
            Len[i]++;//判断当前点是不是最长回文子串，不断的向右扩展
        if(Len[i]+i>mx){//如果当前以i为中心点加上长度后比之前处理出来的mx要大，即越过了边界
            mx=Len[i]+i;//更新mx
            id=i;//更新此时的中间点id
            maxx=max(maxx,Len[i]);//更新最长回文字串长度
        }
    }
    return maxx-1;
}
int main(){
    char c;
    while((c=getchar())!='
')
        s[len++]=c;
    initStr();//重定义字符串
    printf("%d
",manacher());
    return 0;
}

例题 ZOJ 4110