基础算法--树的概述

树的具体的定义不说了，说几个重要的树的性质

一棵树是N个节点和N-1条边的集合，因为除了根节点以外的每一个节点都通过一条边连接到它的父亲节点，所以有N-1条边。

对于任意节点n，n的深度为从根节点到这个节点的唯一路径的长度（长度就是边的个数）。

对于任意节点n，n的高度为从n到一片树叶的最长路径的长度。一棵树的高等于它的根的高。

结点的层次从根开始定义起，根为第一层，根的孩子为第二层。

如果将树中的结点的各子树看成从左到右是有次序的，不能交换的，则称该树为有序树，否则称为无序树。

树的存储结构

说到了存储结果，我们熟悉的无非就是顺序存储结构和链式存储结构。

用一段地址连续的存储单元依次存储线性表的数据元素，这对于线性表很自然，但是对于一对多的树结构，简单的顺序存储结构是不能满足要求的。但是在原来的顺序存储结构上做一些trick还是可以做到的。下面要介绍三种不同的树的表示方法：双亲表示法、孩子表示法、孩子兄弟表示法。

双亲表示法

以一组连续空间存储树的结点，同时在每个结点中，增加一个指示器来指示其双亲结点在数组中的位置。

双亲表示法

data

parent

双亲表示法的结点结构定义代码：

/*树的双亲表示法结点结构定义*/
#define MAX_TREE_SIZE 100
typedef int TElemType;	/*树结点的数据类型，目前定义为整型*/
typedef struct PTNode	/*结点结构*/
{
	TElemType data;	/*结点数据*/
	int parent;	/*双亲位置*/
}PTNode;


typedef struct PTree	/*树结构*/
{
	PTNode nodes[MAX_TREE_SIZE];	/*结点数组*/
	int r,n;	/*根结点位置和结点树*/
}

　　同时，由于树的根结点没有双亲，所以我们约定根节点的位置域设置为-1，代表没有双亲结点。这就意味着所有的结点都存有它的双亲的位置。

如下图，按照从上到下，从左到右的顺序依次存放树的结点：

这样的存储结构，拿到一个结点，很容易根据这个结点的parent指针找到它的双亲结点。并且顺着往上找，一直找到parent为-1时，也就找到了树的根。可是如果想知道这个结点的孩子是谁，那么就得要遍历整个数组了。

为了能克服上面结构的却缺点，为结点增加一个指针域，指向该结点最左边的孩子，不妨叫它长子域，这样就很容易的得到了该结点的一个孩子了。如果没有孩子的结点，这个长子域就设置为-1。

这样对于有0个或者1个孩子的结点来说，这样的结构解决了找孩子的问题，甚至具有2个孩子的结点，知道了长子是谁，那么数组的下一个元素就是次子了（因为结点是从上到下从左到右的顺序存放的）。

如果我们关心某个结点的兄弟是谁，那么就可以这样设计结点结构：

如果，我关注结点的双亲、结点的孩子、结点的兄弟，而且对时间遍历要求还高，那么就可以把结点结构设计成这个样子：

data

parent

firstChild

rightSib

所以数据结构是很灵活的，根据具体的问题，设计具体的数据结构，没有一成不变的东西。

孩子表示法

 在介绍真正的孩子表示法之前，先来说一下两种方案，作为孩子表示法的引出。

方案一：

每个结点的指针域的个数等于树的度，树的度是树中各个结点度的最大值。

data

child1

child2

child3

......

childn

这种方法对于树中各结点的度相差很大时，显然很浪费空间，于是提出方案二。

方案二：

每个结点的指针域的个数等于该结点的度，同时专门设置一个位置来存储结点指针域的个数。

data

degree

child1

child2

......

childn

这种方案虽然克服了空间浪费，但是由于各个结点的链表的结构不同，加上要维护每个结点的度degree的值，所有带来时间上的损耗。

孩子表示法方案:

为了要遍历整棵树，把每个结点放到一个顺序存储结构的数组中，但是每个结点的孩子的数目是不确定的，所以我们再对每个结点的孩子建立一个单链表体现他们的关系。

这样的话，就需要定义两种结点结构，一个是孩子链表的孩子结点：

child

next

另一个就是表头数组的表头结构：

data	firstchild

所以结点结构的定义代码：

#define MAX_TREE_SIZE 100
typedef struct CTNode	/*孩子结点*/
{
	int child;
	struct CTNode *next;
}CTNode;

typedef struct CTBox	/*表头结构*/
{
	TElemType data;
	struct CTNode *firstChild;
};

typedef struct CTree	/*树结构*/
{
	CTBox nodes[MAX_TREE_SIZE];	/*结点数组*/
	int r,n;	/*根的位置和结点数*/
}CTree;

　　这样就能很方便的找到某个结点的孩子，只需要找这个结点的单链表就可以了，也很容易遍历整个树。但是如果想找某个结点的双亲结点，似乎有点困难。

最后我们把双亲表示法和孩子表示法结合一下得到孩子双亲表示法：

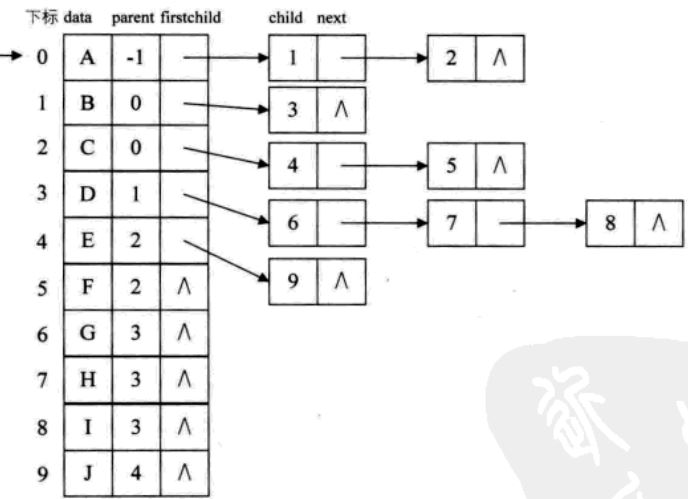
孩子兄弟表示法

任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在就是唯一的，因此得到了孩子兄弟表示法：

data

firstChild

rightsib

结点结构的定义代码：

/*树的孩子兄弟表示法结点结构定义*/
typedef struct CSNode
{
	TElemType data;
	struct CSNode *firstChild, *rightSib;
}CSNode;

　　

如果真的有必要向找某个结点的双亲结点，大不了就为每个结点再增加一个指针域parent指向该结点的双亲结点。其实这个表示法的最大的好处是把一个复杂的树变成了一个二叉树。

 树结构的具体应用

树的应用很多，比较流行的就是UNIX、DOS等许多的常用的操作系统的目录结构，如下面的图所示：

 

看到这是一个很一般的树结构，现在要用程序把它当做一个Unix的目录结构来遍历一下，在Unix的终端中我们可以利用cd命令在各个目录中切换。cd ..命令表示回到当前目录的上一次，cd /表示回到根目录，同时ls命令能看到该目录的所有子目录。所以这个树结构的应用关心结点的双亲结点、结点的所有孩子结点、结点的兄弟结点（关心孩子结点必然是通过长子的兄弟结点找到其他的孩子结点）。

所以知道了需求之后，就要选一种最合适的树结构结点结构的定义方式。其实三种结点结构表示方法都是合适的，这里我选用孩子双亲表示法，就是孩子表示法和双亲表示法的综合。

既然选择了双亲孩子表示法，选定了数据结构和结点的表示方式，下面就开始结点结构的定义代码：

#define MAX_TREE_SIZE 100

typedef struct CTNode *PCTNode;
typedef struct CTNode	/*孩子结点*/
{
	int child;
	PCTNode next;
}CTNode;

typedef struct CTBox	/*表头结构*/
{
	string data;
	int parent;
	PCTNode firstChild;
}CTBox;

typedef struct CTree	/*树结构*/
{
	CTBox nodes[MAX_TREE_SIZE];	/*结点数组*/
	int r,n;	/*根的位置和结点数*/
}CTree;

　　定义好了结点结构的表示方法，下面就看一下遍历各个结点的方法：

这段代码基于上面数据结构的实现代码：

//定义一棵全局的树
CTree cTree;
//定义孩子链表用到的结点数组
CTNode cTNode[10];

void PrintDirName(string strDirectoryName, int depth)
{
	for(int i = 0; i < depth; i++)
	{
		cout << "	";
	}
	
	cout << strDirectoryName << endl;
}

void ListDir(int nodeId, int depth)
{
	if(nodeId >= 0 && nodeId <= cTree.n -  1)
	{
		string str = cTree.nodes[nodeId].data;
		PrintDirName(str, depth);
		
		PCTNode ptrTNode = cTree.nodes[nodeId].firstChild;
		while(ptrTNode != NULL)
		{
			ListDir(ptrTNode->child, depth + 1);
			ptrTNode = ptrTNode->next;
		}
	}
}

void ListDirectory()
{
	int nodeId = 0;//数组下标为0的那个元素存储的就是根节点
	int depth = 0;	//定义根节点的深度为0，这个depth的作用就是在不同层次的目录打印不同的制表符	
	
	ListDir(nodeId, depth);
}

　　为了简单，在源代码中手动初始化一下一棵树，然后测试算法：

void main()
{
	//按照图中初始化孩子结点
	cTNode[0].child = 1;
	cTNode[0].next  = &cTNode[1];

	cTNode[1].child = 2;
	cTNode[1].next  = &cTNode[2];

	cTNode[2].child = 3;
	cTNode[2].next  = NULL;

	cTNode[3].child = 4;
	cTNode[3].next  = &cTNode[4];

	cTNode[4].child = 5;
	cTNode[4].next  = &cTNode[5];

	cTNode[5].child = 6;
	cTNode[5].next  = NULL;

	cTNode[6].child = 7;
	cTNode[6].next  = &cTNode[7];

	cTNode[7].child = 8;
	cTNode[7].next  = NULL;

	cTNode[8].child = 9;
	cTNode[8].next  = &cTNode[9];

	cTNode[9].child = 10;
	cTNode[9].next  = NULL;

	//初始化头结点的数据
	cTree.nodes[0].data = "usr";
	cTree.nodes[0].parent = -1;
	cTree.nodes[0].firstChild = &cTNode[0];
	
	cTree.nodes[1].data = "market";
	cTree.nodes[1].parent = 0;
	cTree.nodes[1].firstChild = &cTNode[3];

	cTree.nodes[2].data = "course";
	cTree.nodes[2].parent = 0;
	cTree.nodes[2].firstChild = NULL;

	cTree.nodes[3].data = "bill";
	cTree.nodes[3].parent = -0;
	cTree.nodes[3].firstChild = &cTNode[6];

	cTree.nodes[4].data = "ch1.r";
	cTree.nodes[4].parent = 1;
	cTree.nodes[4].firstChild = NULL;

	cTree.nodes[5].data = "ch2.r";
	cTree.nodes[5].parent = 1;
	cTree.nodes[5].firstChild = NULL;

	cTree.nodes[6].data = "ch3.r";
	cTree.nodes[6].parent = 1;
	cTree.nodes[6].firstChild = NULL;

	cTree.nodes[7].data = "work";
	cTree.nodes[7].parent = 3;
	cTree.nodes[7].firstChild = &cTNode[8];

	cTree.nodes[8].data = "ch6.r";
	cTree.nodes[8].parent = 3;
	cTree.nodes[8].firstChild = NULL;

	cTree.nodes[9].data = "ch4.r";
	cTree.nodes[9].parent = 7;
	cTree.nodes[9].firstChild = NULL;

	cTree.nodes[10].data = "ch5.r";
	cTree.nodes[10].parent = 7;
	cTree.nodes[10].firstChild = NULL;

	cTree.n = 11;
	cTree.r = 0;


	ListDirectory();

}

　　算法代码的运行结果

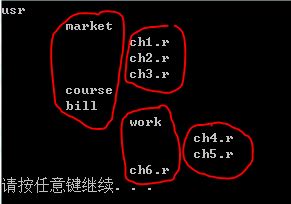
验证完了上面的代码，现在再来看另外的一个需求，需要统计每个目录占用的磁盘块数，文件夹也占用一个磁盘块的。如下图所示：

 

再来看一下后序遍历的方法：

算法的代码实现：

void PrintDirInfo(string strDirectoryName, int depth, int block)
{
	cout << block;

	for(int i = 0; i < depth; i++)
	{
		cout << "	";
	}
	
	cout << strDirectoryName << endl;
}//PrintDirInfo
int SizeDirectory(int nodeId, int depth)
{
	int totalSize = 0;

	if(nodeId >= 0 && nodeId <= cTree.n -  1)
	{
		string str = cTree.nodes[nodeId].data;
		totalSize = cTree.nodes[nodeId].block;
		
		PCTNode ptrTNode = cTree.nodes[nodeId].firstChild;
		while(ptrTNode != NULL)
		{
			totalSize += SizeDirectory(ptrTNode->child, depth + 1);
			ptrTNode = ptrTNode->next;
		}
		PrintDirInfo(str, depth, totalSize);
	}

	return totalSize;
}//SizeDirectory()

　　结点结构定义中，在数据结点中增加一个表示磁盘块的int block变量，在main函数的测试代码中按照上图中的数值初始化一下，就可以继续跑起来了。

看一下运行结果：

总结

 上面的代码的结点结构的表示方法用的是双亲表示和孩子表示法的综合，当然也可以利用双亲结点表示法和孩子兄弟表示法的综合，算法的实现大体相似，这里就不另写一个了。上面的两个算法的不同之处就是问题的需求不同，所用到的树的遍历的方式不同，第一个题目用到了树的先序遍历，后面的一个题目用到了树的后序遍历。

返回目录链接：基础算法--树