863. 二叉树中所有距离为 K 的结点 力扣（中等） bfs

题目描述：

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

示例 1：

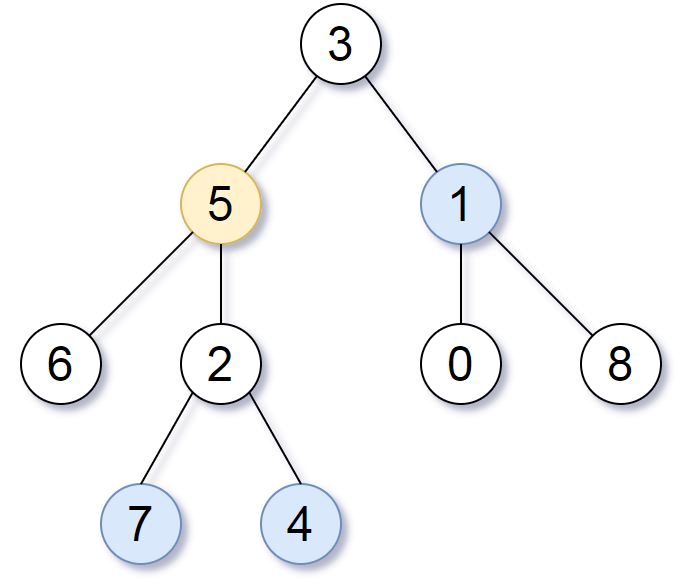
输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1

 

注意，输入的 "root" 和 "target" 实际上是树上的结点。上面的输入仅仅是对这些对象进行了序列化描述。

题源：

题解：

先将树转化成图，然后进行bfs遍历，耗时8ms, 内存消耗12.9M

代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
    vector<int> res;
    if(k==0)
    {
        res.push_back(target->val);
        return res;
    }
    map<int,vector<int>> mp;   //  因为节点值唯一，可以构造关系矩阵
    queue<TreeNode*> Q;
    Q.push(root);
    while(!Q.empty())
    {
        TreeNode* p=Q.front();
        Q.pop();
        if(p->left!=NULL)
        {
            Q.push(p->left);
            mp[p->val].push_back(p->left->val);
            mp[p->left->val].push_back(p->val);
        }
        if(p->right!=NULL)
        {
            Q.push(p->right);
            mp[p->val].push_back(p->right->val);    //父亲节点连接右儿子节点
            mp[p->right->val].push_back(p->val);   // 儿子节点记录父亲节点
        }
    }
    
    queue<int> Q2;   //开始bfs遍历
    vector<int> sublevel;
    Q2.push(target->val);
    int step=0,l=1;
    bool flag[505];
    memset(flag,0,sizeof(flag)); //标记是否被访问过
    flag[target->val]=1;
    while(!Q2.empty())
    {
        sublevel.clear(); 
        for(int i=0;i<l;i++)
        {
            int p=Q2.front();
            Q2.pop();
            for(auto j:mp[p])
            {
                if (flag[j]) continue;
                sublevel.push_back(j);
                Q2.push(j);
                flag[j]=1;   // 不能忘记标记
            }
        }
        step++;
        l=sublevel.size();
        if(step==k) break;
    }
        return sublevel;
    }
};