Minimal Ratio Tree
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other)
Total Submission(s) : 12 Accepted Submission(s) : 7
Font: Times New Roman | Verdana | Georgia
Font Size: ← →
Problem Description
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
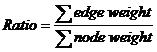
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
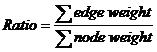
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input
Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
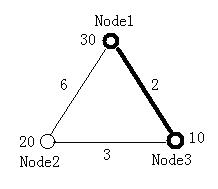
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output
For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .
Sample Input
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
Sample Output
1 3 1 2
#include <iostream> #include<cstdio> #include<cstring> #include<climits> using namespace std; int a[20],f[20],p[20]; int mp[20][20]; bool vis[20]; int i,j,n,m; double ans; void prim() //最小生成树 { bool vis[20]; int dis[20]; int sumnode,sumedge=0,k; memset(vis,0,sizeof(vis)); vis[1]=1; sumnode=p[a[1]]; for(int i=1;i<=m;i++) dis[i]=mp[a[1]][a[i]]; for(int i=1;i<m;i++) { int minn=INT_MAX; for(int j=1;j<=m;j++) { if (!vis[j] && dis[j]<minn) { minn=dis[j]; k=j; } } vis[k]=1; sumedge+=minn; sumnode+=p[a[k]]; for(int j=1;j<=m;j++) if (!vis[j] && dis[j]>mp[a[k]][a[j]]) dis[j]=mp[a[k]][a[j]]; } double w=sumedge*1.0/sumnode; if (w<ans) //把最优解存放在f数组中 { ans=w; for(int i=1;i<=m;i++) f[i]=a[i]; } return; } void dfs(int k,int num)//dfs暴力枚举m个节点是哪几个存在a数组中 { if (num==m) { prim(); return; } if (k>n) return; if (!vis[k]) { vis[k]=1; a[num+1]=k; dfs(k+1,num+1); vis[k]=0; } dfs(k+1,num); return; } int main() { while(scanf("%d%d",&n,&m)) { if (n==0 && m==0) break; for(i=1;i<=n;i++) scanf("%d",&p[i]); for(i=1;i<=n;i++) for(j=1;j<=n;j++) scanf("%d",&mp[i][j]); memset(vis,0,sizeof(vis)); ans=INT_MAX*1.0; dfs(1,0); for(i=1;i<m;i++) printf("%d ",f[i]); printf("%d\n",f[m]); } return 0; }