要求:
1.输入一个二维整形数组主,数组里有正数也有负数。
2.二维数组中连续的一个子矩阵组成一个子矩阵组成一个子数组,每个子数组都有一个和。
思路:根据上次写的找一维数组中最大子数组的经验,不妨把二维数组转化为一维数组的形式先进行求和,再比较,选出最大的子数组。首先以第一行为上界,依次向下确定数组的最大范围,把最大子数组按照一列有几个数,分成几种不同的行,对于产生数组的,进行一维数组求和计算并找出最大值。然后将上界下调一行,从第二行开始,依次向下确定数组最大范围,重复以上步骤。
代码如下:
#include<iostream>
using namespace std;
void main ()
{
int x,y,i,j,m=0,A[100][100];
cout<<"输入矩阵的行和列:";
cin>>x>>y;
if(x>100||y>100)
{
cout<<"请重新输入:";
cin>>x>>y;
}
for(i=0;i<x;i++)
{
for(j=0;j<y;j++)
{
cin>>A[i][j];
}
}
int sum[100]={0},max=0,result=A[0][0];
for(i=0;i<x;i++)
{
while(m+i<x)
{
for(j=0;j<y;j++)
{
sum[j]=sum[j]+A[m+i][j];
}
max=0;
for(j=0;j<y;j++)
{
if(max+sum[j]>sum[j])
{
max=max+sum[j];
}
else
{
max=sum[j];
}
if(max>result)
{
result=max;
}
}
m++;
}
m=0;
for(j=0;j<y;j++)
{
sum[j]=0;
}
}
cout<<result;
system("pause");
}
运行结果:
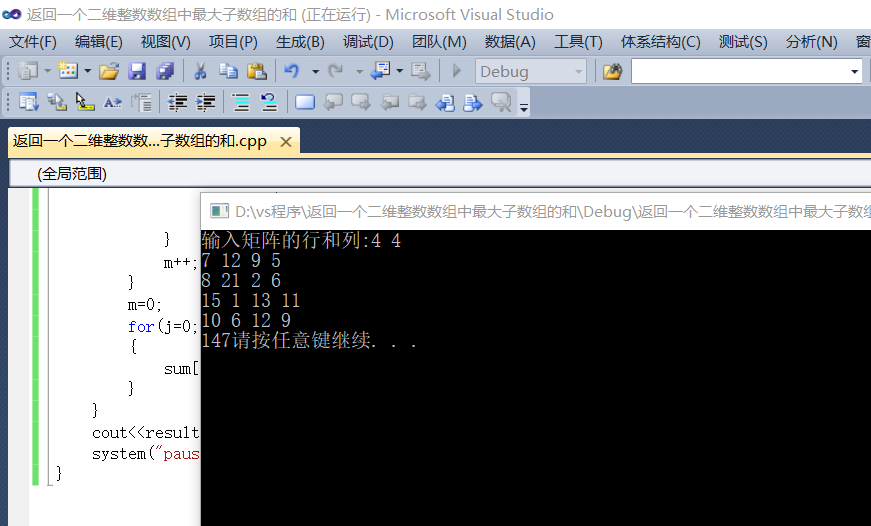

总结:这个方法有些类似枚举法,就算是枚举,它应当有按一定的规则进行,所以我们给它定制特点的选取数组方法。本次任务对于我和我的伙伴来说有很大的难度,我们一起探讨思路探讨了很久,彼此在决定方案的时候有一些分歧,在编写程序的过程中也有一些矛盾,比如我们在时间上有一些不同步,比如我们在任务分配上有一些不同意见,比如我们在策略决定上有一些不同想法。但是我们有着同一个目的,同样的解决问题的决心,也有着对彼此的宽容。最终我们完成了这项任务。

