简化电梯调度算法
GitHub: https://github.com/StolfdaInuit/object-oriented
| 编写程序的代码行数 | 调试的bug数 | 完成该次作业总耗时 |
|---|---|---|
| 245 + 265行 | 10 ~ 20个 | 12 ~ 15h |
文件清单
...elevator-scheduling
// A策略:选取当前 向上、向下、停靠 三类行动中让另外两类行动的乘客等待时间最小的一个
-> A.cpp
// B策略:估计三种行动的耗时,采用预估耗时最少的
-> B.cpp
// 可预知,暴力求解
-> test.cpp
优化过程
问题给出的目标是实现一个简化的电梯调度算法,要求尽可能使乘客等待总时长最短。考虑到电梯不能预知请求,推测可能不存在针对所有情况的唯一最优解。
所以如果根据唯一的要求让乘客等待总时长尽可能短来分析,不考虑电梯节能归位之类的因素,普通电梯的SCAN算法是不满足的,应该采取贪心策略,设定一些权值来判断。
一开始的思路就是为每个乘客的行动添加权值,然后统计归类,确定局部最优。
然而如何设定合适的权值计算公式这一步让我思考了很久,试了好几种方案。
改进策略的方法是自己做一些数据手动模拟测试。
试了一些数据感觉没什么问题之后,总结了下策略:
选取当前 向上、向下、停靠 三类行动中让另外两类行动的乘客等待时间最小的一个
确定好这个方案之后,就正式开始用C++实现了,IDE是VS2017。
写完大概一百行,然后开始测试数据,结果全是死循环。
fix掉几个粗心bug后发现还是死循环。
认真研究了一下,发现是最重要的选取策略实现有问题。应该对0人的情况进行特判,并且权值相同时优先满足人多的。
修修补补,加了一大段代码后,终于能正常运行了。
做了几个特殊边界情况的数据,果然又出现bug了:A策略无法中途掉头。
在某些特殊的情况下,为了满足多数人的需求,或者两拨人方向相异时,应当能够中途掉头来取得最优时间。
改了一天,重构了整个算法,甚至把核心策略改成了:
估计三种行动的耗时,采用预估耗时最少的
虽然自以为新策略应该更优一些,也能够解决之前发现的问题,但实际上在随机的5组数据里,2组更优,2组不变,1组更差。
于是干脆把新策略命名为plan B,和之前的plan A一起塞到github上去了。
之后又试着写了未卜先知的电梯,确定最优解来比对,方法是生成全排列全部方案走一遍,找到最优的。因为算法太暴力,所以跑起来很慢。
测试数据
数据1:目的信息同时出现,电梯应当达到理论最优解
0 5 1
5 4 1
5 2 0
5 6 0
5 8 1
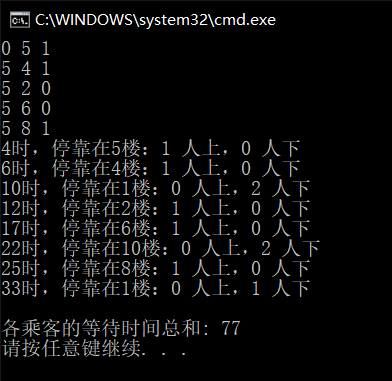
测试结果:
B.cpp:77
得到最优解,符合预测
数据2:电梯应当能够在运行中掉头才能得到最优解
0 1 0
0 1 0
0 1 0
0 1 0
2 2 1

测试结果:
B.cpp:58
中途掉头,符合预测
数据3:电梯应当不在运行中掉头才能得到最优解
0 1 0
0 1 0
0 1 0
0 1 0
5 2 1
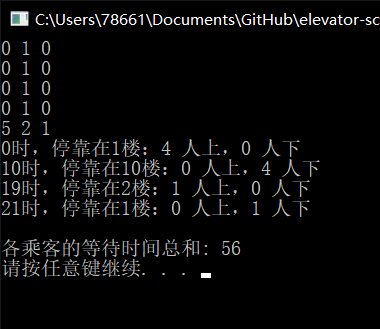
测试结果:
B.cpp:56
中途不掉头,符合预测
数据4:不同时间,同起点出发,应当尽可能搭载多个同目的地乘客
0 5 0
3 5 1
6 5 0
9 5 1
12 5 0
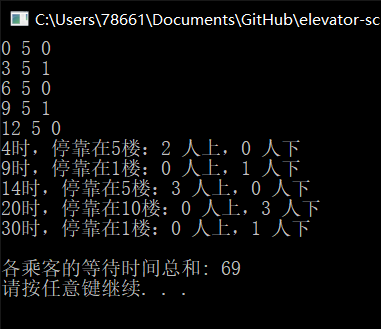
测试结果:
B.cpp:69
符合预测
数据5:随机的较大数据,观察是否出现异常
666 3 0
667 7 1
660 5 1
663 8 0
673 1 0
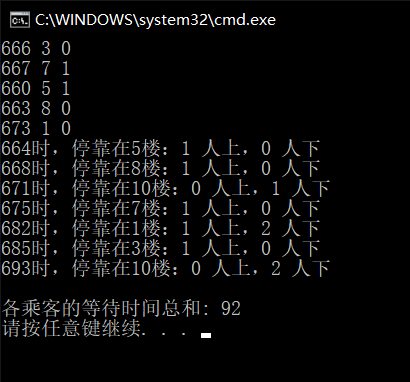
测试结果:
B.cpp:92
电梯正常,结果可以接受
Pintia小作业