题目
题目链接:https://www.luogu.com.cn/problem/P1447
栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量。在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐,一共有 \(n\) 列,每列有 \(m\) 棵,植物的横竖间距都一样,因此对于每一棵植物,栋栋可以用一个坐标 \((x, y)\) 来表示,其中 \(x\) 的范围是 \(1\) 至 \(n\),\(y\) 的范围是 \(1\) 至 \(m\),表示是在第 \(x\) 列的第 \(y\) 棵。
由于能量汇集机器较大,不便移动,栋栋将它放在了一个角上,坐标正好是 \((0, 0)\)。
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有 \(k\) 棵植物,则能量的损失为 \(2k + 1\)。例如,当能量汇集机器收集坐标为 \((2, 4)\) 的植物时,由于连接线段上存在一棵植物 \((1, 2)\),会产生 \(3\) 的能量损失。注意,如果一棵植物与能量汇集机器连接的线段上没有植物,则能量损失为 \(1\)。现在要计算总的能量损失。
下面给出了一个能量采集的例子,其中 \(n = 5\),\(m = 4\),一共有 \(20\) 棵植物,在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
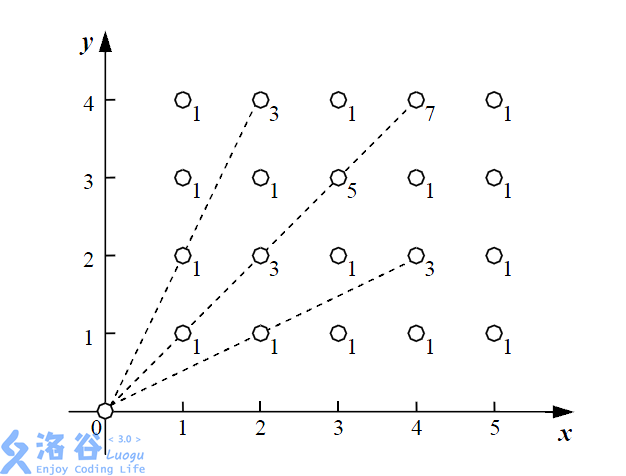
在这个例子中,总共产生了 \(36\) 的能量损失。
思路
容易发现点 \((x,y)\) 到点 \((0,0)\) 路径上有 \(\gcd(x,y)\) 个点(包括 \((x,y)\))。所以答案为
设 \(f(i)\) 表示 \(\gcd(x,y)=i\) 的方案数,有
答案即为
甚至不用整除分块,直接算即可。
时间复杂度 \(O(n\log n)\)。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
int n,m,cnt,mu[N],prm[N];
ll ans,sum;
bool v[N];
void findprm(int n)
{
mu[1]=1;
for (int i=2;i<=n;i++)
{
if (!v[i])
prm[++cnt]=i,mu[i]=-1;
for (int j=1;j<=cnt;j++)
{
if (1LL*i*prm[j]>n) break;
v[i*prm[j]]=1; mu[i*prm[j]]=-mu[i];
if (!(i%prm[j]))
{
mu[i*prm[j]]=0;
break;
}
}
}
}
int main()
{
findprm(N-1);
scanf("%d%d",&n,&m);
for (int i=1;i<=min(n,m);i++)
{
sum=0;
for (int j=i;j<=min(n,m);j+=i)
sum+=1LL*mu[j/i]*(n/j)*(m/j);
ans+=sum*i;
}
printf("%lld\n",ans*2LL-1LL*n*m);
return 0;
}