★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
➤微信公众号:山青咏芝(shanqingyongzhi)
➤博客园地址:山青咏芝(https://www.cnblogs.com/strengthen/)
➤GitHub地址:https://github.com/strengthen/LeetCode
➤原文地址:https://www.cnblogs.com/strengthen/p/11032155.html
➤如果链接不是山青咏芝的博客园地址,则可能是爬取作者的文章。
➤原文已修改更新!强烈建议点击原文地址阅读!支持作者!支持原创!
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
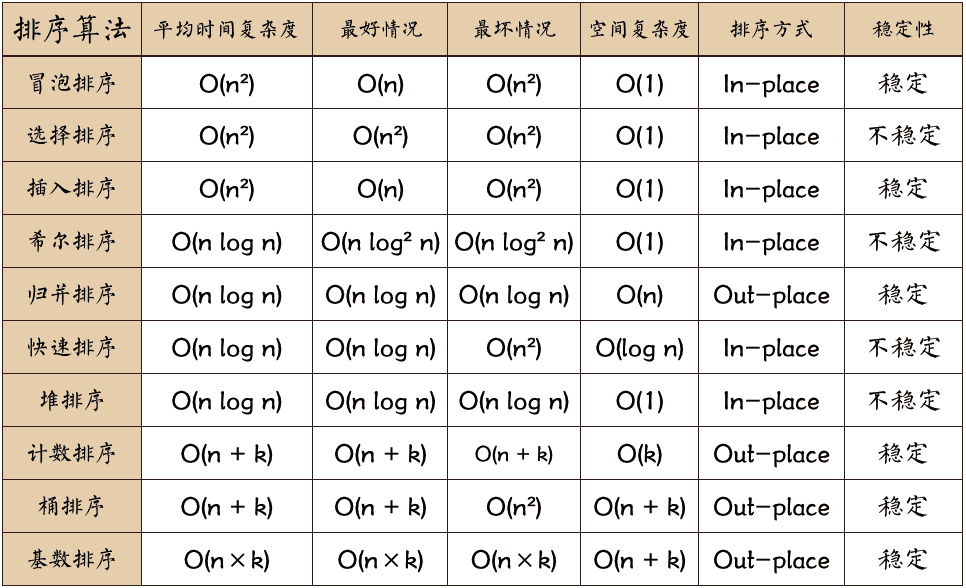
1、鸡尾酒排序,也称双向冒泡排序,是冒泡排序的究极进化版本,是稳定的比较排序算法。该算法与冒泡排序不同之处在于:在数组的两个方向上进行排序。它可以实现比标准冒泡排序稍好的性能。但它只提供了微小的性能改进,并没有改善渐近性能;和冒泡排序一样,鸡尾酒排序没有实际意义,它只在算法教育中有一定作用。插入排序是简单排序的首选
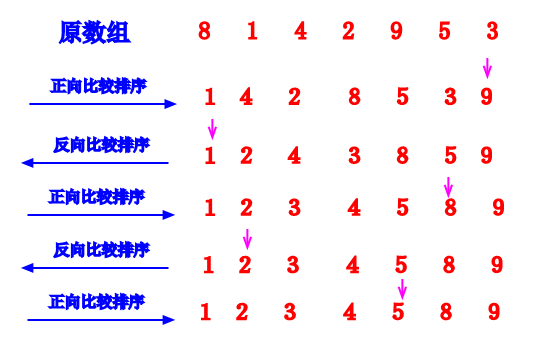

2、与冒泡排序的区别:通常鸡尾酒排序比冒泡排序快两倍。
例如:对[2,3,4,5,1]进行排序:
鸡尾酒排序只需排序一次,
升序冒泡排序需要排序四次。
3、鸡尾酒排序优化:
排序中记住最后一次实际交换的位置。在下一次迭代中,将没有超出此限制的交换。当鸡尾酒排序按双向排序时,可能的交换范围(即待测范围)将通过每次减少,从而略微减少整体运行时间。但是这些改进都不会导致该算法比插入排序更好。
4、Talk is cheap.Show me your code:
1 //MARK:鸡尾酒排序 2 func cocktailSort(_ arr:inout [Int]) 3 { 4 var left:Int = 0 5 var right:Int = arr.count - 1 6 while (left < right) 7 { 8 for i in left..<right 9 { 10 if arr[i] > arr[i + 1] 11 { 12 arr.swapAt(i,i + 1) 13 } 14 } 15 right -= 1 16 for i in stride(from:right,to:left,by:-1) 17 { 18 if arr[i - 1] > arr[i] 19 { 20 arr.swapAt(i,i - 1) 21 } 22 } 23 left += 1 24 } 25 }
5、测试
1 var arr:[Int] = [1,9,2,8,3,7,4,6,5,10,11,12] 2 cocktailSort(&arr) 3 print(arr) 4 //Print [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]