学习数据结构和算法要从复杂度分析说起。表示时间的大O符号,是用来描述算法效率的语言和度量单位。算法复杂度包括时间复杂度和空间复杂度,两者中又以时间复杂度相对重要,因为就 Web 应用而言,我们常见的性能优化策略都是以空间换时间,比如缓存系统就是如此。
时间复杂度表示代码执行时间随数据规模增长的变化趋势,表示方法图所示:
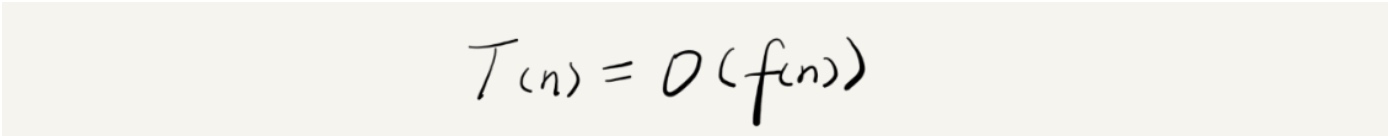
即大O表示法,我们在分析时间复杂度的时候往往遵循以下原则:
- 1、只关注循环执行次数最多的一段代码;
- 2、加法法则:总复杂度等于量级最大的那段代码的复杂度;
- 3、乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。
常见时间复杂度如下所示:

注意事项:
- 常量不算在运算时间里。
例如某个O(2N)的算法实际上是O(N)。特定输入中,O(N)很有可能会比O(1)代码还要快。大O仅仅描述了增长的趋势。
- 丢弃不重要的项
应该舍弃无关紧要的项。比如 O(N2+N)变成O(N2)、O(N+logN)变成O(N)、O(5*2^N+1000N^100)变成O(2^N)等。
- logN运行时间
元素的个数每次减半,它的运行时间很可能是O(logN)。
以二分查找为例。假设一个排序数组长度为N,目标值为x。首先比较x与中值,如果x等于中值直接返回,如果小于中值,搜索数组的左边,如果大于中值,搜索数组的右边。
开始时有N个元素的排序数组要搜索,经过一次搜索之后,还剩下N/2个元素,再一次,剩下N/4个元素,直到找到目标值或者待搜索元素个数为1时才停止搜索。
同理,在平衡二叉搜索树中查找一个元素也是O(logN),每次比较,非左即右。
- 递归的运行时间
当一个多次调用自己的递归函数出现时,它的运行时间往往是O(分支数^数的深度),分支数即每次调用自己的次数。
例如:
int f(int n) { if (n <= 1) { return 1; } return f(n-1) + f(n-1); }
运行时间是O(2^N)。
这个例子的空间复杂度为O(N),尽管树节点总数为O(2^N),但同一时刻只有O(N)个节点存在。
再例如:
把平衡二叉搜索树上所有节点的值相加,运行时间是多少?
分支树是2,深度大概是logN,所以为O(2^logN) = O(N) , 运行时间是O(N)。