今天开始,我们将花三篇文章的篇幅由浅及深地介绍几个字符串匹配算法,首先从最简单的字符串匹配算法 —— BF 算法说起,BF 是 Brute Force 的缩写,中文译作暴力匹配算法,也叫朴素匹配算法。
BF算法(暴力匹配算法)
BF 算法的原理很简单,在继续介绍之前,我们先引入两个术语:主串和模式串。简单来说,我们要在字符串 A 中查找子串 B,那么 A 就是主串,B 就是模式串。
作为最简单、最暴力的字符串匹配算法,BF 算法的思想可以用一句话来概括,那就是,如果主串长度为 n,模式串长度为 m,我们在主串中检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟模式串匹配的。图示如下:

结合上图,具体来说,就是每次拿模式串和主串对齐,然后从左到右依次比较每个字符,如果出现不相等,则把模式串往后移一个位置,再次重复上述步骤,直到模式串每个字符与对应主串位置字符都相等,则返回主串对应下标,表示找到,否则返回 -1,表示没找到。
这个算法很好理解,因为这就是我们正常都能想到的暴力匹配,BF 算法的时间复杂度最差是 O(n*m),意味着要模式串要移到主串 n-m 的位置上,并且模式串每个字符都要与子串比较。
尽管 BF 算法复杂度看起来很高,但是在日常开发中,如果主串和模式串规模不大的话,该算法依然比较常用,因为足够简单,实现起来容易,不容易出错。另外,在规模不大的情况下,开销也可以接受,毕竟 O(n*m) 是最差的表现,大部分时候,执行效率比这个都要高。
但是对于对时间要求比较敏感,或者需要高频匹配,数据规模较大的情况下,比如编辑器中的匹配功能、敏感词匹配系统等,BF 算法就不适用了。
KMP算法(Knuth Morris Pratt 算法)
KMP 算法可以说是字符串匹配算法中最知名的算法了,KMP 算法是根据三位作者(D.E.Knuth,J.H.Morris 和 V.R.Pratt)的名字来命名的,算法的全称是 Knuth Morris Pratt 算法,简称为 KMP 算法。
KMP 算法的核心思想
假设主串是 a,模式串是 b。在模式串与主串匹配的过程中,当遇到不可匹配的字符的时候,我们希望找到一些规律,可以将模式串往后多滑动几位,跳过那些肯定不会匹配的情况,从而避免 BF 算法这种暴力匹配,提高算法性能。下面我们来探讨下这个规律如何找到。
参考下面个主串和模式串的匹配,当模式串移动到当前位置,比对到最后一个字符 D 时,发现与主串不匹配,如果按照 BF 算法,就是把模式串往后移一位,再逐个比较,这样做固然可以,但是效率很差:

一个基本事实是,当 D 与主串不匹配时,我们已知前面的主串序列是 ABCDA,如果把模式串往后移一位肯定和主串不匹配,我们可不可以直接把模式串移到下一个可能和 A 匹配的主串位置?
实际上,KMP 算法正是基于这一理念,设法利用这个已知信息,不把模式串移到已经比较过的位置,继续把它向后移,这样综合下来就极大提高了搜索匹配效率。
怎么找到这个规律,确定把模式串往后移多少位呢?在模式串和主串匹配的过程中,我们把不能匹配的那个字符仍然叫作「坏字符」,把已经匹配的那段字符串叫作「好前缀」:
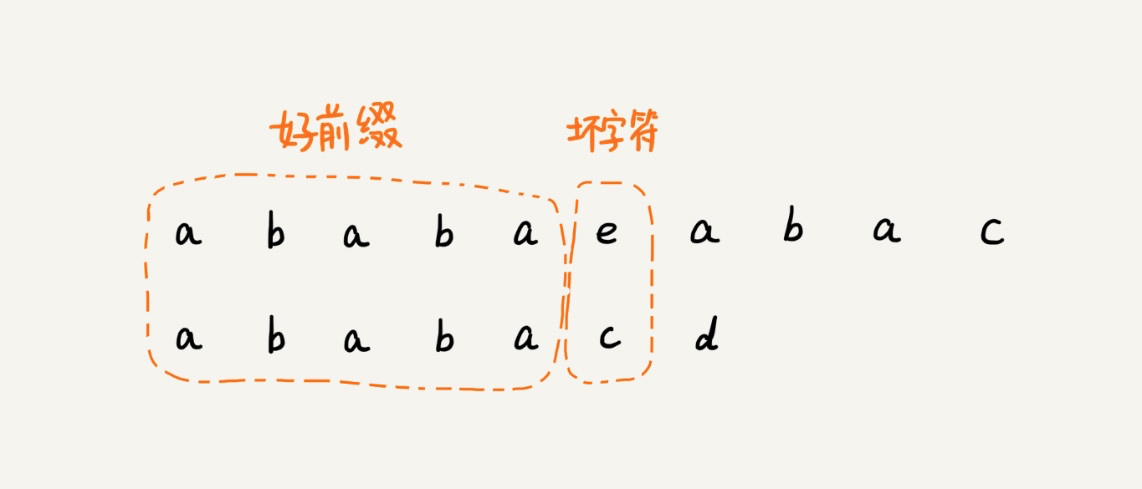
在模式串和主串匹配的过程中,当遇到坏字符后,对于已经比对过的好前缀,我们只需要拿好前缀本身,在它的后缀子串中,查找最长的那个可以跟好前缀的前缀子串匹配的下标位置,然后将模式串后移到该位置即可。
这里,我们要解释几个概念:
- 后缀子串:以某个字符串最后一个字符为尾字符的子串(不包含字符串自身),比如上面的
ababa,后缀子串为baba、aba、ba、a; - 前缀子串:以某个字符串第一个字符为首字符的子串(不包含字符串自身),还是以
ababa为例,前缀子串为a、aba、abab; - 最长可匹配后缀子串:后缀子串与前缀子串最长可匹配子串,也可叫做共有子串,以
ababa为例,自然是aba了,长度为 3; - 最长可匹配前缀子串:与上面定义相对,即前缀子串与后缀子串最长可匹配子串。最长可匹配前缀子串和最长可匹配后缀子串肯定是一样的。
假设坏字符所在位置是 j,最长可匹配后缀子串长度为 k,则模式串需要后移的位数为 j-k。每当我们遇到坏字符,就将模式串后移 j-k 位,直到模式串与对应主串字符完全匹配;如果移到最后还是不匹配,则返回 -1。这就是 KMP 算法的核心思想。
KMP 算法的实现
了解了核心思想,接下来,就可以考虑如何实现 KMP 算法了,实现 KMP 算法最核心的部分是构建一个用来存储模式串中每个前缀子串(这些前缀都有可能是好前缀)最长可匹配前缀子串的结尾字符下标数组,我们把这个数组叫做 next 数组,对于上面 ababacd 这个模式串而言,对应的 next 数组如下:
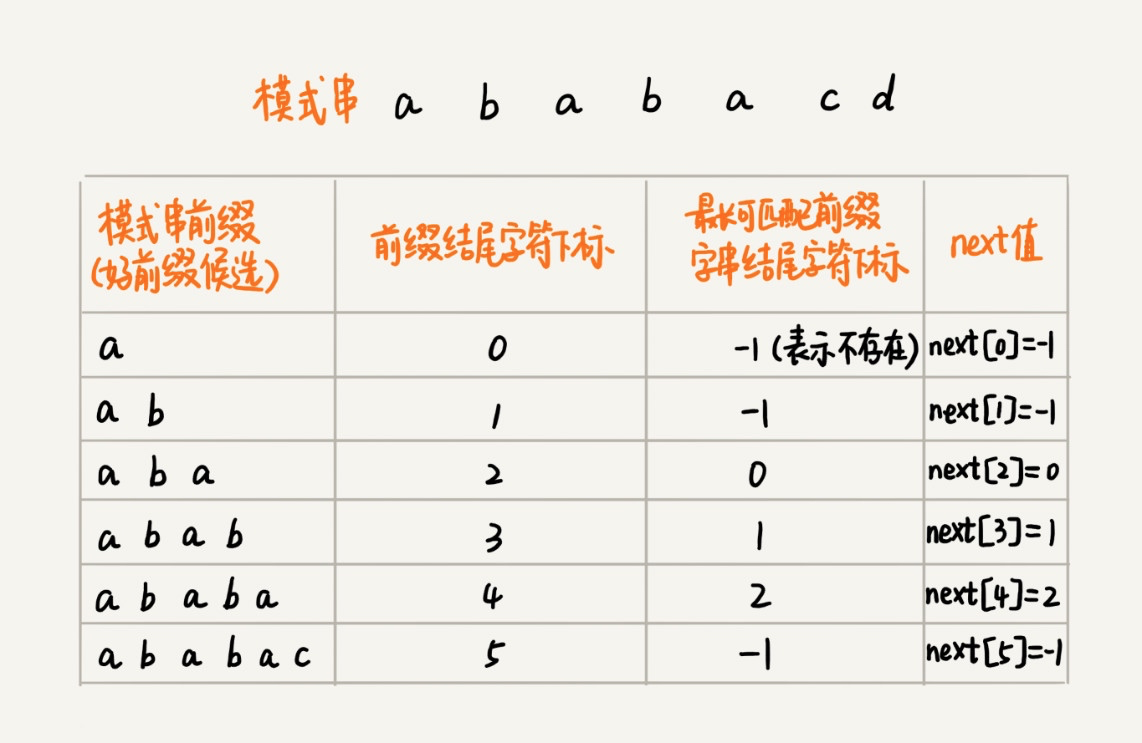
其中,数组的下标是前缀子串结尾字符下标,数组的值是这个前缀的最长可匹配前缀子串的结尾字符下标。
有了这个 next 数组,我们就可以实现 KMP 匹配算法的核心代码了:
/ KMP 算法 PHP 实现代码,$a 表示主串,$n 表示主串长度,$b 表示模式串,$m 表示模式串长度
function kmp($a, $n, $b, $m)
{
$next = generateNexts($b, $m); // 生成 next 数组
$j = 0;
for ($i = 0; $i < $n; $i++) { // 遍历主串
while ($j > 0 && $a[$i] != $b[$j]) {
// 如果主串字符和模式串字符不相等,
// 更新模式串坏字符下标位置为好前缀最长可匹配前缀子串尾字符下标+1
// 然后从这个位置重新开始与主串匹配
// 相当于前面提到的把模式串向后移动 j - k 位
$j = $next[$j - 1] + 1;
}
if ($a[$i] == $b[$j]) {
$j++;
}
if ($j == $m) {
return $n - $m + 1; // 全部相等,找到匹配位置
}
}
return -1;
}
接下来就是如何生成 next 数组了,这一步是最难的,我们现在可以参考上面 next 数组生成原理通过循环比对前缀子串和后缀子串的方式去理解,毕竟我们在实际开发中不太可能自己去实现 KMP 算法,了解原理即可,以后说到动态规划,会用动态规划来实现它。这里就不再深入探究了。
Trie 树的定义、实现及应用
Trie 树的定义
Trie 树,也叫「前缀树」或「字典树」,顾名思义,它是一个树形结构,专门用于处理字符串匹配,用来解决在一组字符串集合中快速查找某个字符串的问题。
注:Trie 这个术语来自于单词「retrieval」,你可以把它读作 tree,也可以读作 try。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起,比如我们有["hello","her","hi","how","seo","so"] 这个字符串集合,可以将其构建成下面这棵 Trie 树:
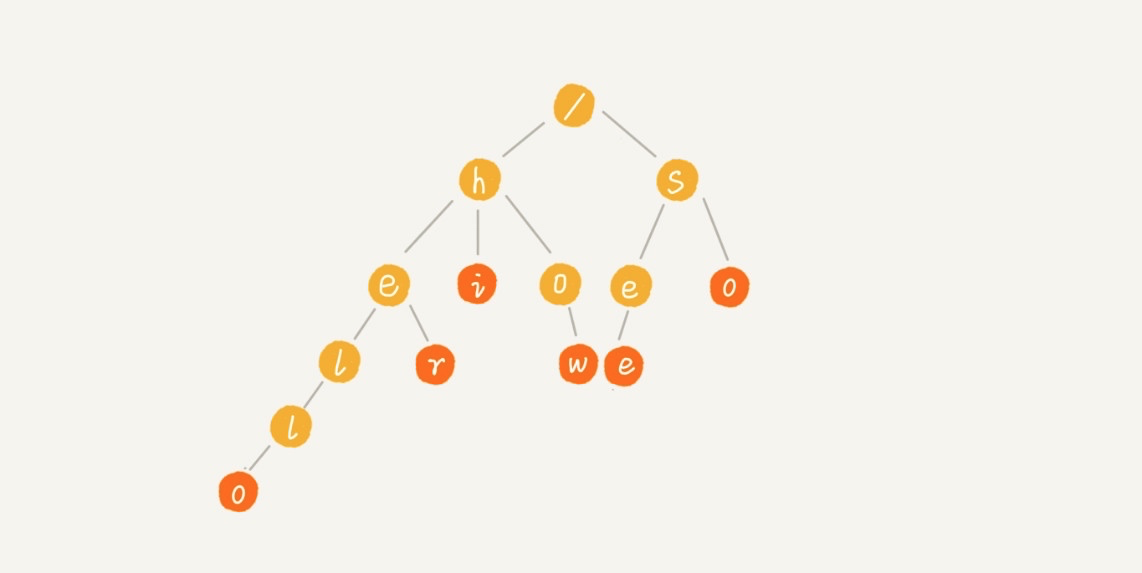
每个节点表示一个字符串中的字符,从根节点到红色节点的一条路径表示一个字符串(红色节点表示是某个单词的结束字符,但不一定都是叶子节点)。
这样,我们就可以通过遍历这棵树来检索是否存在待匹配的字符串了,比如我们要在这棵 Trie 树中查询 her,只需从 h 开始,依次往下匹配,在子节点中找到 e,然后继续匹配子节点,在 e 的子节点中找到 r,则表示匹配成功,否则匹配失败。通常,我们可以通过 Trie 树来构建敏感词或关键词匹配系统。
如何实现 Trie 树
从刚刚 Trie 树的介绍来看,Trie 树主要有两个操作,一个是将字符串集合构造成 Trie 树。这个过程分解开来的话,就是一个将字符串插入到 Trie 树的过程。另一个是在 Trie 树中查询一个字符串。
Trie 树是个多叉树,二叉树中,一个节点的左右子节点是通过两个指针来存储的,对于多叉树来说,我们怎么存储一个节点的所有子节点的指针呢?
我们将 Trie 树的每个节点抽象为一个节点对象,对象包含的属性有节点字符、子节点引用和是否是字符串结束字符标志位:
class TrieNode
{
public $data; // 节点字符
public $children = []; // 存放子节点引用(因为有任意个子节点,所以靠数组来存储)
public $isEndingChar = false; // 是否是字符串结束字符
public function __construct($data)
{
$this->data = $data;
}
}
要构造一棵完整的 Trie 树,关键在于存储子节点引用的 $children 属性的实现。借助散列表的思想,我们通过一个下标与字符一一映射的数组,来构造 $children:我们将字符串中每个字符转化为 ASCII 码作为数组下标,将对应节点对象引用作为数组值,依次插入所有字符串,从而构造出 Trie 树。对应 PHP 实现代码如下:
class Trie
{
private $root;
public function __construct()
{
$this->root = new TrieNode('/'); // 存储无意义字符
}
// 往 Trie 树中插入一个字符串
public function insert(array $text)
{
$p = $this->root;
for ($i = 0; $i < count($text); $i++) {
$index = ord($text[$i]) - ord('a');
if ($p->children[$index] == null) {
$newNode = new TrieNode($text[$i]);
$p->children[$index] = $newNode;
}
$p = $p->children[$index];
}
$p->isEndingChar = true;
}
// 在 Trie 树中查找一个字符串
public function find(array $pattern)
{
$p = $this->root;
for ($i = 0; $i < count($pattern); $i++) {
$index = ord($pattern[$i]) - ord('a');
if ($p->children[$index] == null) {
// 不存在 pattern
return false;
}
$p = $p->children[$index];
}
if ($p->isEndingChar == false) {
return false; // 不能完全匹配,只是前缀
}
return true; // 找到 pattern
}
}
但是这个 Trie 树只适用于 ASCII 编码字符,无法对更加复杂的字符集进行操作。对于 PHP 数组来说,我们完全可以将每个字符值作为下标,因为 PHP 数组本身就是散列表,这样就可以上述实现改造为直接支持中文的字符串匹配,改造后的代码如下:
class PhpTire
{
private $root;
public function __construct()
{
$this->root = new TrieNode('/'); // 存储无意义字符
}
// 往 Trie 树中插入一个字符串
public function insert($text)
{
$p = $this->root;
for ($i = 0; $i < mb_strlen($text); $i++) {
$index = $data = $text[$i];
if ($p->children[$index] == null) {
$newNode = new TrieNode($data);
$p->children[$index] = $newNode;
}
$p = $p->children[$index];
}
$p->isEndingChar = true;
}
// 在 Trie 树中查找一个字符串
public function find($pattern)
{
$p = $this->root;
for ($i = 0; $i < mb_strlen($pattern); $i++) {
$index = $pattern[$i];
if ($p->children[$index] == null) {
// 不存在 pattern
return false;
}
$p = $p->children[$index];
}
if ($p->isEndingChar == false) {
return false; // 不能完全匹配,只是前缀
}
return true; // 找到 pattern
}
}
我们可以编写一段简单的测试代码:
$trie = new PhpTire();
$strs = ['Laravel', 'PHP汉子', 'Framework', 'Hyperf', 'MixPHP', 'Swoole'];
foreach ($strs as $str) {
$trie->insert($str);
}
if ($trie->find('汉子')) {
print '包含这个字符串';
} else {
print '不包含这个字符串';
}
结果会返回 不包含这个字符串。
Trie 树的复杂度
构建 Trie 树的过程比较耗时,对于有 n 个字符的字符串集合而言,需要遍历所有字符,对应的时间复杂度是 O(n),但是一旦构建之后,查询效率很高,如果匹配串的长度是 k,那只需要匹配 k 次即可,与原来的主串没有关系,所以对应的时间复杂度是 O(k),基本上是个常量级的数字。
Trie 树显然也是一种空间换时间的做法,构建 Trie 树的过程需要额外的存储空间存储 Trie 树,而且这个额外的空间是原来的数倍。
你会发现,通过 Trie 树进行字符串匹配和之前介绍的 BF 算法和 KMP 算法有所不同,BF 算法和 KMP 算法都是在给定主串中匹配单个模式串,而 Trie 树是将多个模式串与单个主串进行匹配,因此,我们将 BF 和 KMP 这种匹配算法叫做单模式匹配算法,而将 Trie 树这种匹配算法叫做多模式匹配算法。
Trie 树的应用
Trie 树适用于那些查找前缀匹配的字符串,比如敏感词过滤和搜索框联想功能。
1、敏感词过滤系统
一个简单的敏感词过滤系统,就用到了 Trie 树来对敏感词进行搜索匹配:首先运营在后台手动更新敏感词,底层通过 Tire 树构建敏感词库,然后当商家发布商品时,以商品标题+详情作为主串,将敏感词库作为模式串,进行匹配,如果模式串和主串有匹配字符,则以此为起点,继续往后匹配,直到匹配出完整字符串,然后标记为匹配出该敏感词(如果想嗅探所有敏感词,继续往后匹配),否则将主串匹配起点位置往后移,从下一个字符开始,继续与模式串匹配。
2、搜索框联想功能
另外,搜索框的查询关键词联想功能也是基于 Trie 树实现的:
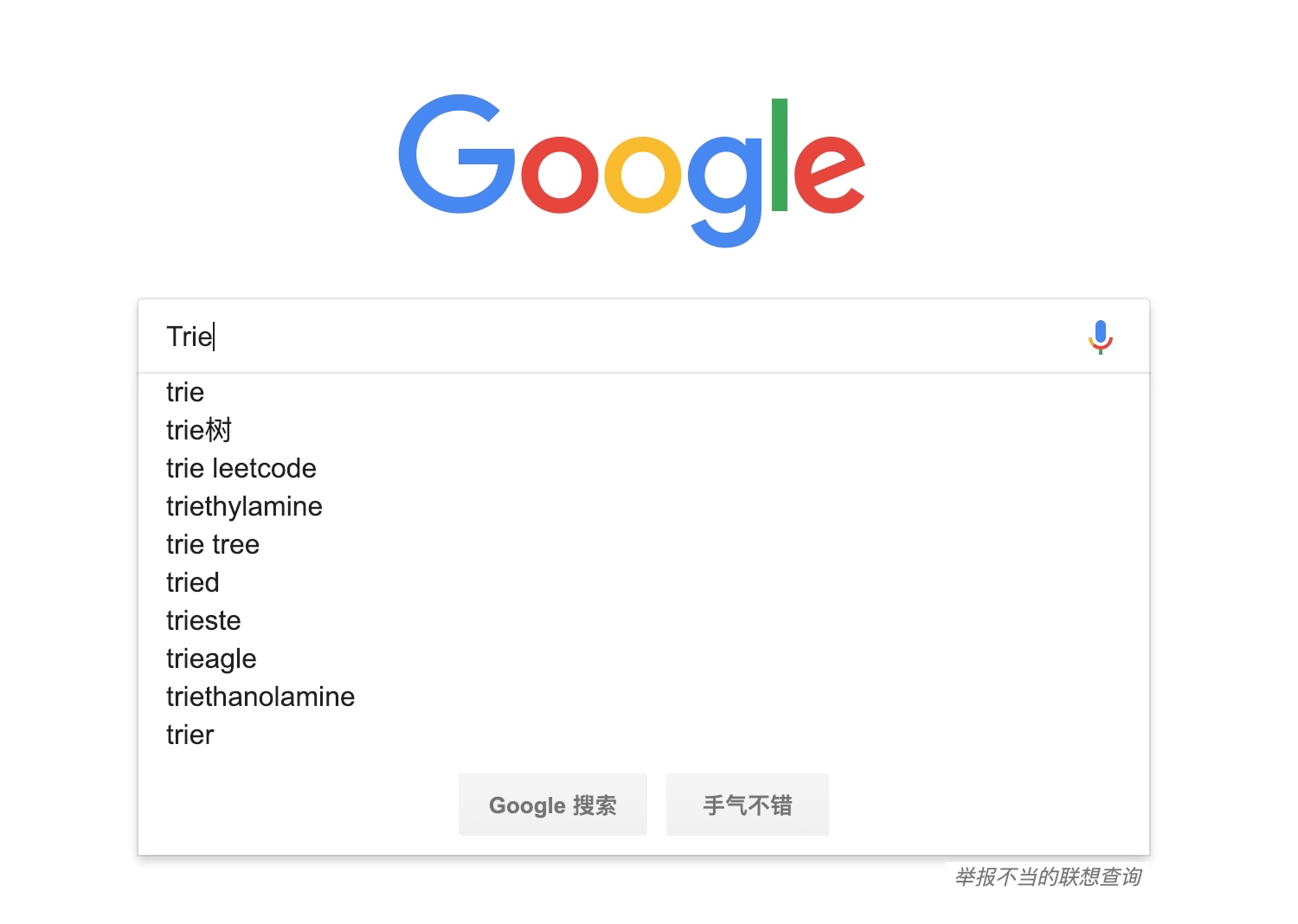
进而可以扩展到浏览器网址输入自动补全、IDE代码编辑器自动补全、输入法自动补全功能等。