前面几篇分享中我们陆续介绍了平衡二叉树的定义、实现原理、构建过程演示以及对应的实现代码,我们提到平衡二叉树是最理想的二叉排序树,性能最好,也最稳定,但是缺点是维护成本高,需要在插入和删除节点时维护新树的平衡性,所以工程实践中,我们倾向于使用另一种二叉排序树 —— 红黑树,什么是红黑树?红黑树的性能如何?如何实现红黑树?
什么是红黑树
红黑树(Red-Black Tree)是每个节点都带有颜色属性的二叉排序(查找)树,具备以下特性:
- 节点是红色或黑色;
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
下面是一个典型的红黑树示例:
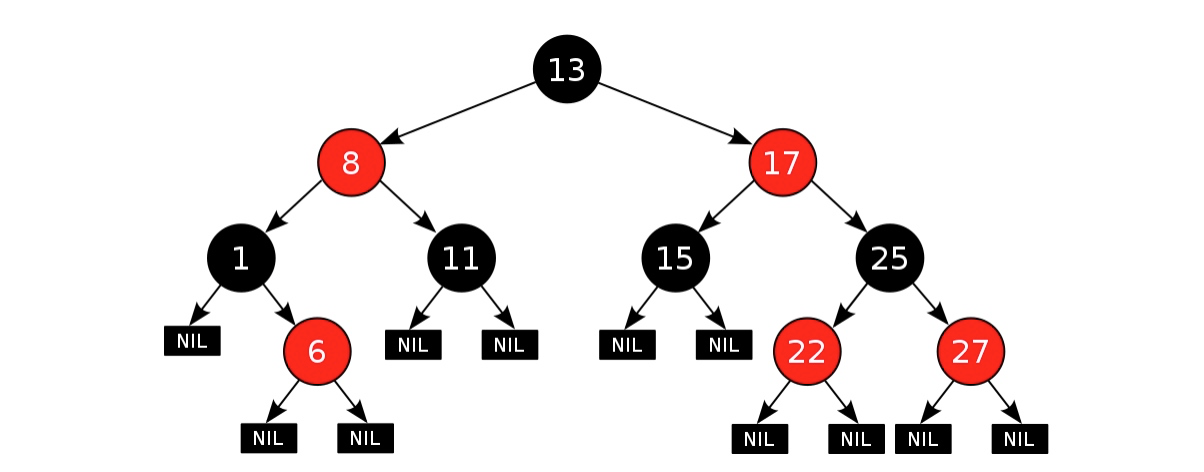
红黑树的算法复杂度
我们上面提到由于红黑树的特性,可以确保即使在最差情况下,红黑树也是大致平衡的,下面我们来简单推导下红黑树的时间复杂度。
前面我们讲二叉排序树的时候说到二叉排序树的时间复杂度和树的高度成正比,红黑树是红黑相间的,我们可以先把红色的节点去掉,剩下的黑色节点就可能变成四叉树了,比如我们上面示例的那个红黑树。由于红黑树每条路径上黑色节点相同,所以可以继续把这个四叉树转化为完全二叉树,假设黑色节点的数量为 m,这样,这棵树的时间复杂度就是 O(logm) 了;然后我们把红色节点塞回来,红色节点的总数目肯定是小于等于黑色节点的,我们不妨假设等于黑色节点,这样,树的高度就增加一倍,对应的时间复杂度就是 2O(logm) 了,m≈n/2,由于在计算时间复杂度的时候,常量可以舍弃,所以红黑树的时间复杂度也是 O(logn)。虽然这里面都是估算的,但是由于前面提到的红黑树的特性约束,数量级上是没问题的。
为什么工程上大多使用红黑树
红黑树维护成本比平衡二叉树低,性能上也能大致做到 O(logn),且比较稳定,可以应付最差的情况。
红黑树的动态平衡实现原理分析
插入节点
红黑树规定,插入的节点必须是红色的。而且,二叉排序(查找)树中新插入的节点都是放在叶子节点上。首先,我们来看两种最简单的情况:
- 如果插入节点的父节点是黑色的,那我们什么都不用做,它仍然满足红黑树的定义。
- 如果插入的节点是根节点,那我们直接把它设置为黑色就可以了。
除此之外,其他情况都会违背红黑树的特性,所以我们需要进行动态调整,与平衡二叉树不同,调整的过程除了左右旋转之外,还涉及到节点颜色的调整。
新节点插入之后,如果红黑树的平衡被打破,那一般会有下面三种情况。我们只需要根据每种情况的特点,不停地调整,就可以让红黑树继续符合定义,也就是继续保持平衡。
有了前面平衡二叉树的铺垫,相信理解起来红黑树的构建过程将会更加轻松。为了方便表述,我们把正在处理的节点叫关注节点。
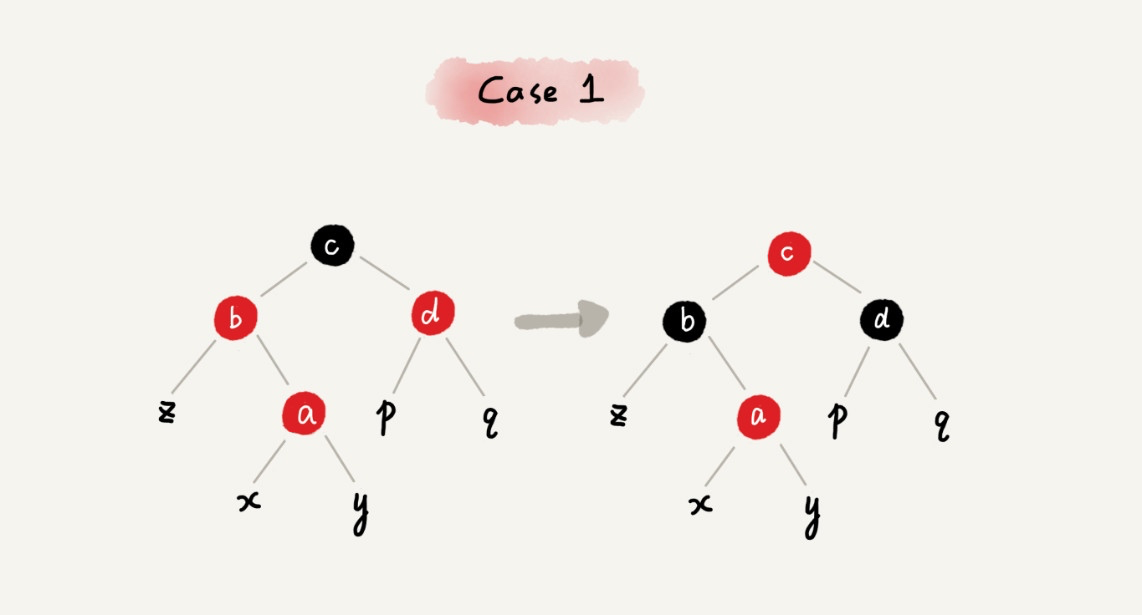
CASE 1:如果关注节点是 a(待插入节点),它的叔叔节点(父亲的兄弟节点,从二叉排序树的角度来说叫伯伯节点更合适?) d 是红色,我们就依次执行下面的操作:
- 将关注节点 a 的父节点 b、叔叔节点 d 的颜色都设置成黑色;
- 将关注节点 a 的祖父节点 c 的颜色设置成红色;
- 关注节点变成 a 的祖父节点 c;
- 跳到下面的 CASE 2 或者 CASE 3 继续处理。
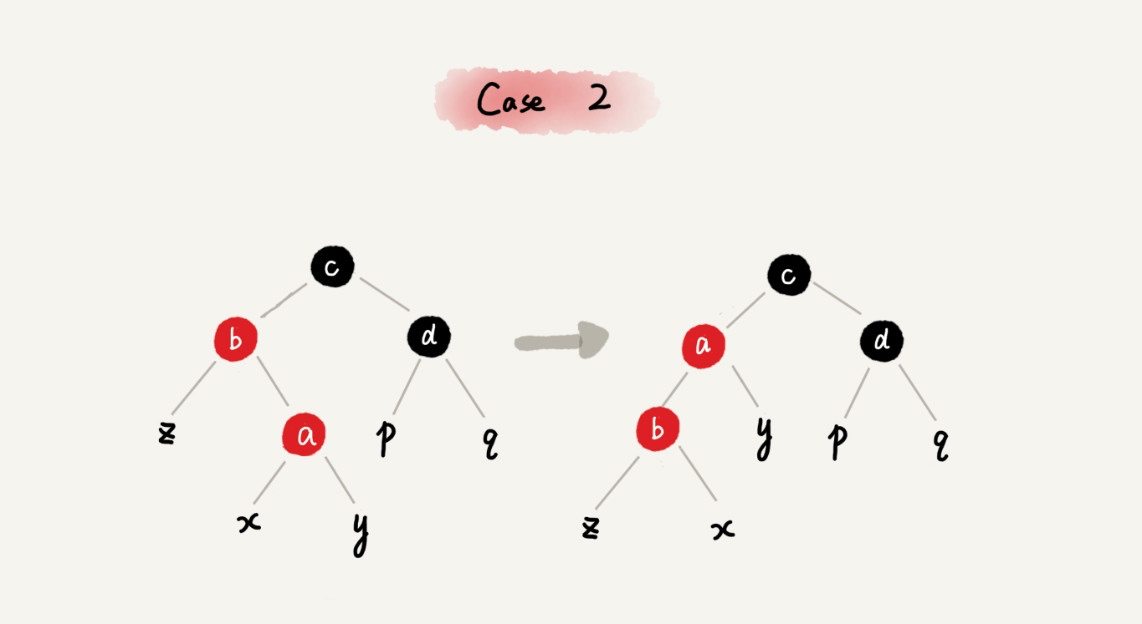
CASE 2:如果关注节点是 a,它的叔叔节点 d 是黑色,关注节点 a 是其父节点 b 的右子节点,我们就依次执行下面的操作:
- 关注节点变成节点 a 的父节点 b;
- 围绕新的关注节点 b 左旋;
- 跳到 CASE 3。
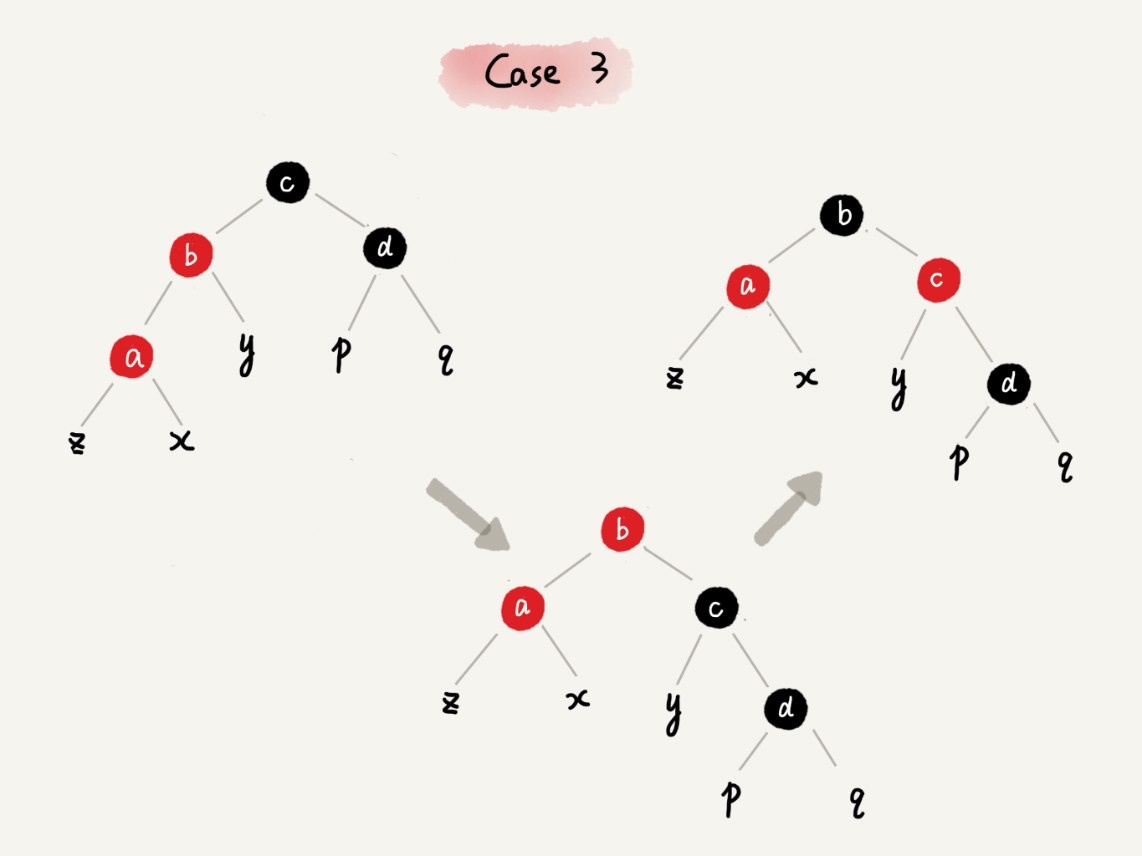
CASE 3:如果关注节点是 a,它的叔叔节点 d 是黑色,关注节点 a 是其父节点 b 的左子节点,我们就依次执行下面的操作:
- 围绕关注节点 a 的祖父节点 c 右旋;
- 将关注节点 a 的父节点 b、兄弟节点 c 的颜色互换。
- 调整结束,至此就构造出来一棵红黑树。
在看上面三个 CASE 的时候要动态的去看,从 CASE 1 跳到 CASE 2 或 CASE 3,或者从 CASE 2 跳到 CASE 3,或者从 CASE 3 开始,不要分割开来。如果从 CASE 1 跳到到 CASE 2 或 CASE 3,后两者的关注节点 a 就是 CASE 1 中最终的关注节点 c。
删除节点
删除节点的平衡调整更加复杂,可以分为两步,第一步是针对删除节点初步调整。初步调整只是保证整棵红黑树在一个节点删除之后,仍然满足最后一条定义的要求,也就是说,每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;第二步是针对关注节点进行二次调整,让它满足红黑树的第三条定义,即不存在相邻的两个红色节点。
1、针对删除节点的初步调整
这里需要注意一下,红黑树的定义中「只包含红色节点和黑色节点」,经过初步调整之后,为了保证满足红黑树定义的最后一条要求,有些节点会被标记成两种颜色,「红-黑」或者「黑-黑」。如果一个节点被标记为了「黑-黑」,那在计算黑色节点个数的时候,要算成两个黑色节点。
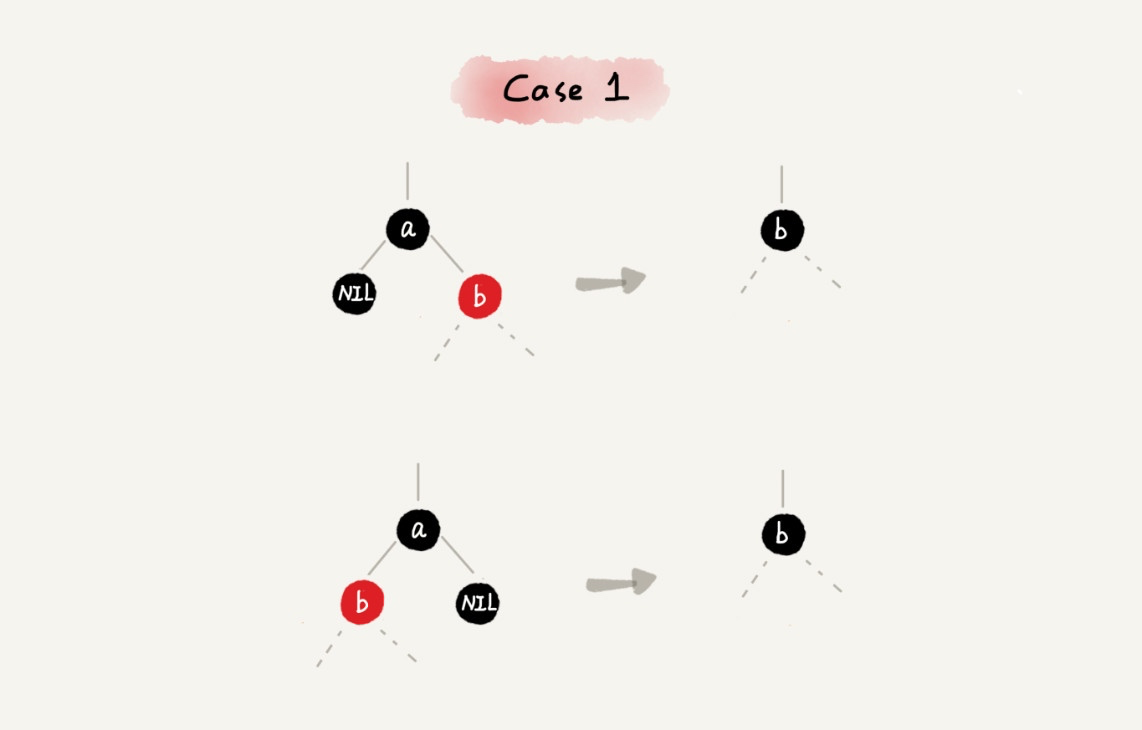
CASE 1:如果要删除的节点是 a,它只有一个子节点 b,那我们就依次进行下面的操作:
- 删除节点 a,并且把节点 b 替换到节点 a 的位置,这一部分操作跟普通的二叉查找树的删除操作一样;
- 节点 a 只能是黑色,节点 b 也只能是红色,其他情况均不符合红黑树的定义。这种情况下,我们把节点 b 改为黑色;
- 调整结束,不需要进行二次调整。
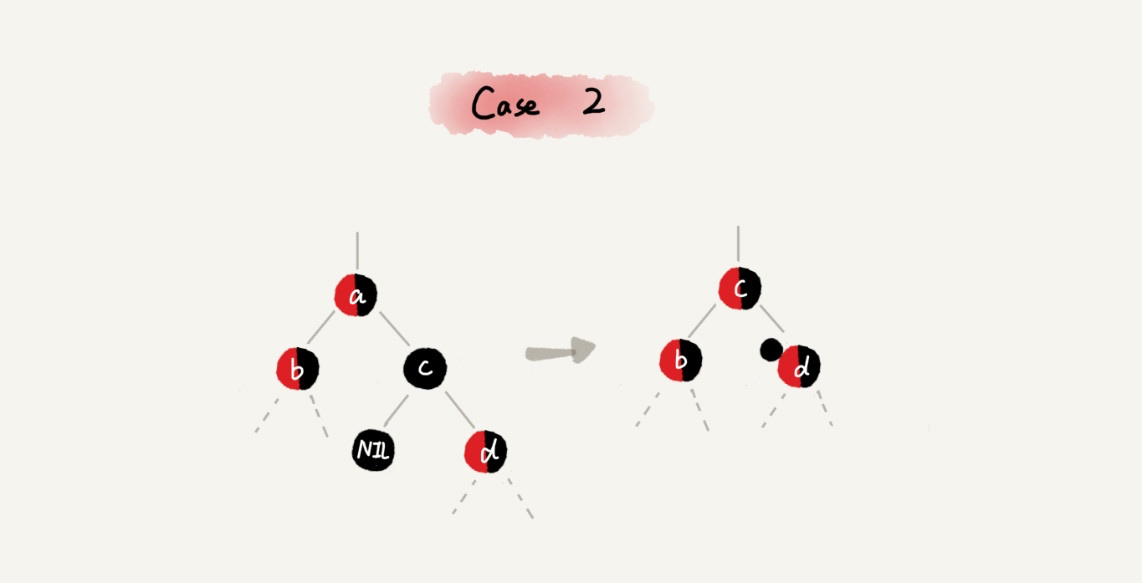
CASE 2:如果要删除的节点 a 有两个非空子节点,并且它的后继节点就是节点 a 的右子节点 c
- 如果节点 a 的后继节点就是右子节点 c,那右子节点 c 肯定没有左子树(否则就不是后继节点了)。我们把节点 a 删除,并且将节点 c 替换到节点 a 的位置。这一部分操作跟普通的二叉查找树的删除操作无异;
- 然后把节点 c 的颜色设置为跟节点 a 相同的颜色;
- 如果节点 c 是黑色,为了不违反红黑树的最后一条定义,我们给节点 c 的右子节点 d 多加一个黑色,这个时候节点 d 就成了「红-黑」或者「黑-黑」;
- 这个时候,关注节点变成了节点 d,第二步的调整操作就会针对关注节点来做。
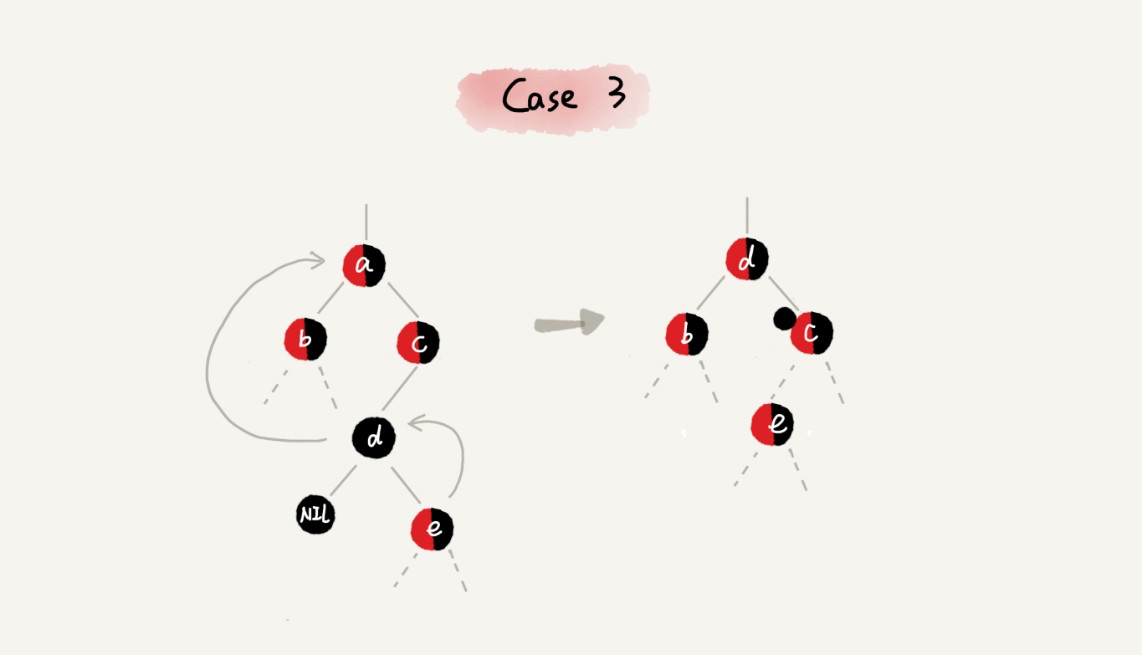
CASE 3:如果要删除的是节点 a,它有两个非空子节点,并且节点 a 的后继节点不是右子节点,我们就依次进行下面的操作:
- 找到后继节点 d,并将它删除,删除后继节点 d 的过程参照 CASE 1;
- 将节点 a 替换成后继节点 d;
- 把节点 d 的颜色设置为跟节点 a 相同的颜色;
- 如果节点 d 是黑色,为了不违反红黑树的最后一条定义,我们给节点 d 的右子节点 c 多加一个黑色,这个时候节点 c 就成了「红-黑」或者「黑-黑」;
- 这个时候,关注节点变成了节点 c,第二步的调整操作就会针对关注节点来做。
2、针对关注节点的二次调整
经过初步调整之后,关注节点变成了「红-黑」或者「黑-黑」节点。针对这个关注节点,我们再分四种情况来进行二次调整。二次调整是为了让红黑树中不存在相邻的红色节点。
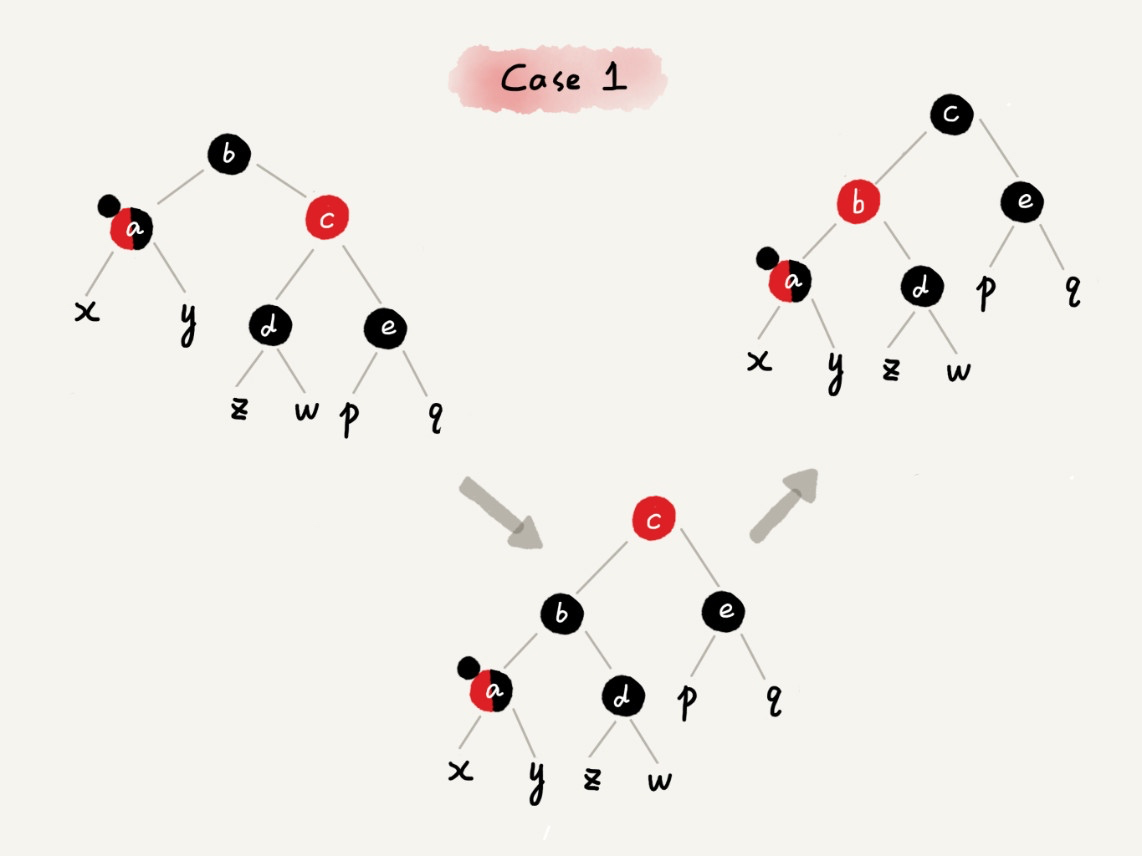
CASE 1:如果关注节点是 a,它的兄弟节点 c 是红色的
- 围绕关注节点 a 的父节点 b 左旋;
- 关注节点 a 的父节点 b 和祖父节点 c 交换颜色;
- 关注节点不变;
- 继续从四种情况中选择适合的规则来调整。
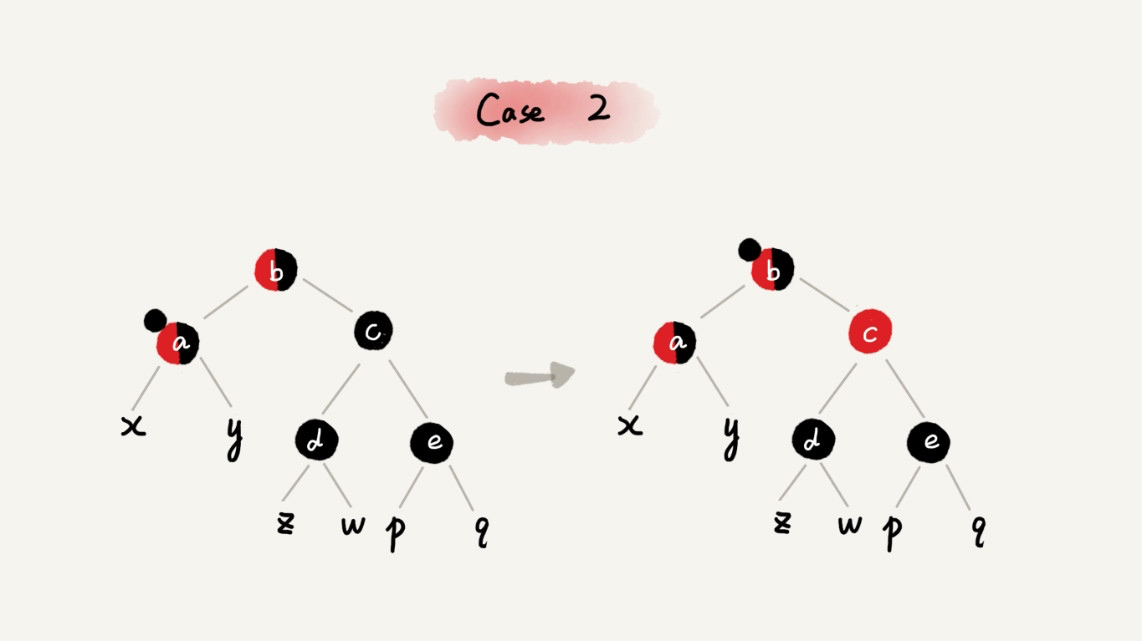
CASE 2:如果关注节点是 a,它的兄弟节点 c 是黑色的,并且节点 c 的左右子节点 d、e 都是黑色的
- 将关注节点 a 的兄弟节点 c 的颜色变成红色;
- 从关注节点 a 中去掉一个黑色,这个时候节点 a 就是单纯的红色或者黑色;
- 给关注节点 a 的父节点 b 添加一个黑色,这个时候节点 b 就变成了「红-黑」或者「黑-黑」;
- 关注节点从 a 变成其父节点 b;
- 继续从四种情况中选择符合的规则来调整。
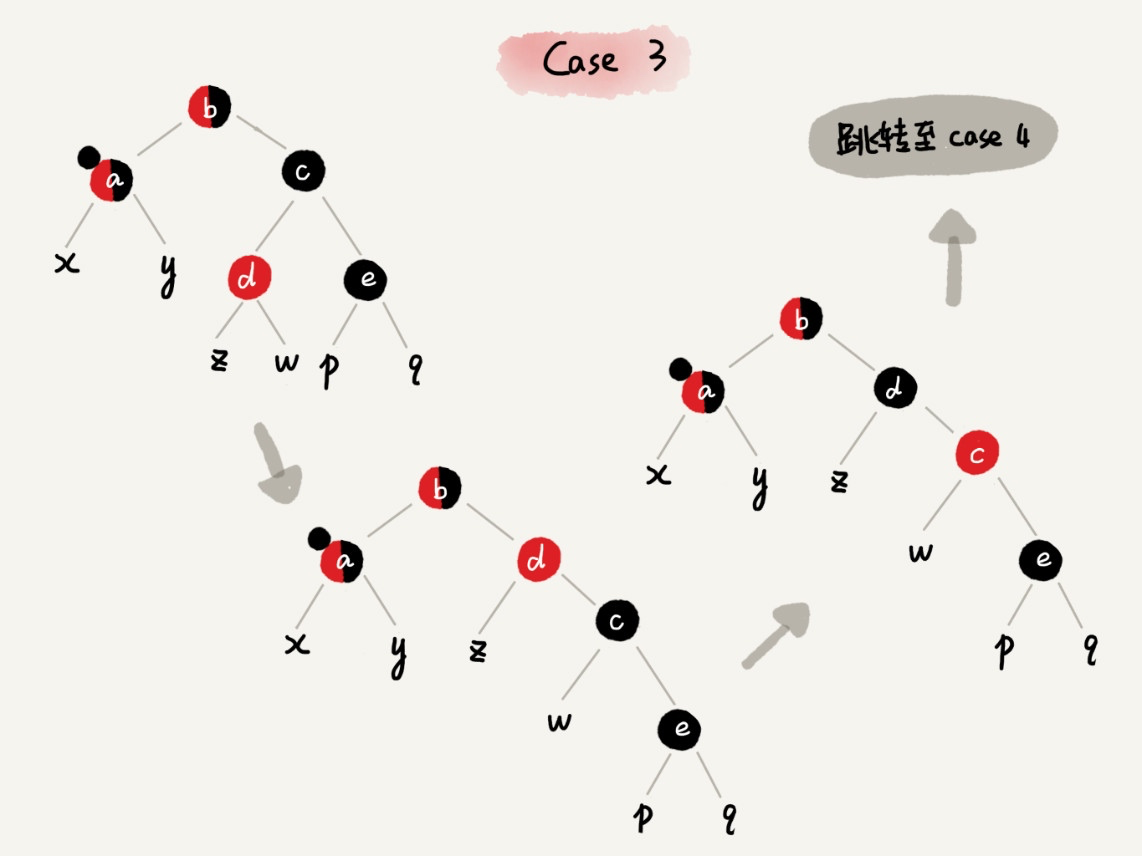
CASE 3:如果关注节点是 a,它的兄弟节点 c 是黑色,c 的左子节点 d 是红色,c 的右子节点 e 是黑色,我们就依次进行下面的操作:
- 围绕关注节点 a 的兄弟节点 c 右旋;
- 节点 c 和节点 d 交换颜色;
- 关注节点不变;
- 跳转到 CASE 4,继续调整。
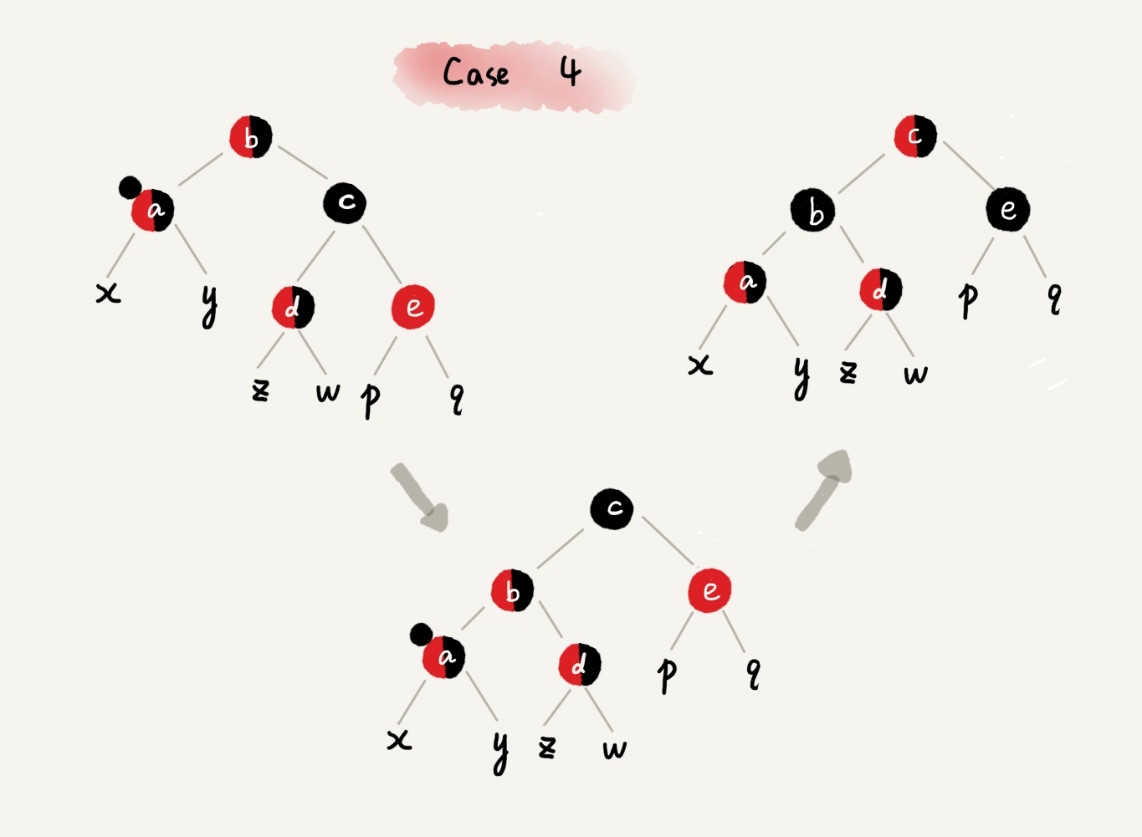
CASE 4:如果关注节点 a 的兄弟节点 c 是黑色的,并且 c 的右子节点是红色的,我们就依次进行下面的操作:
- 围绕关注节点 a 的父节点 b 左旋;
- 将关注节点 a 的兄弟节点 c 的颜色,跟关注节点 a 的父节点 b 设置成相同的颜色;
- 将关注节点 a 的父节点 b 的颜色设置为黑色;
- 从关注节点 a 中去掉一个黑色,节点 a 就变成了单纯的红色或者黑色;
- 将关注节点 a 的叔叔节点 e 设置为黑色;
- 调整结束。
为什么叶子节点都是黑色的空节点
你可能会好奇,为什么叶子节点都是黑色的空节点,其实这就是为了红黑树实现起来更方便。只要满足这一条要求,那在任何时刻,红黑树的平衡操作都可以归结为我们刚刚讲的那几种情况。
不要担心这么做会浪费存储空间,因为其实只要一个空节点就好了:
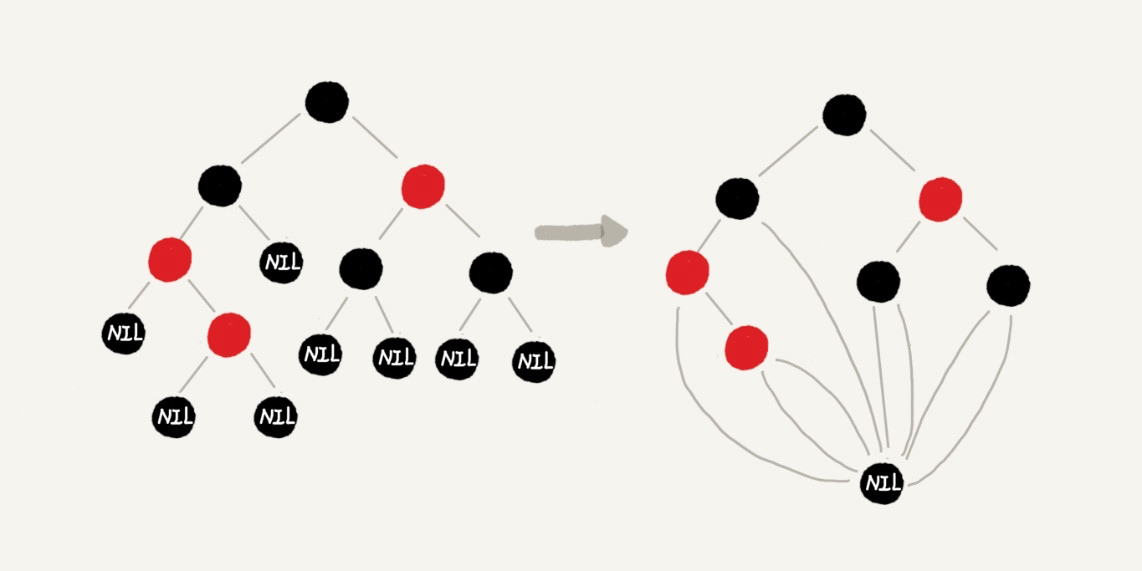
注:以上红黑树的动态平衡过程主要参考了极客时间王争的算法专栏相应教程。关于红黑树的实现原理,了解其大致实现过程就好了,如果觉得复杂,看不懂,也没啥关系,毕竟基本上不会遇到手动实现红黑树的场景。