昨天的judge系统出现问题了,hahahahaha~(导致做题中断了,唉。。。)
今天对一些问题的理解:
1科学计数法(概念,表示方法)
2一元二次方程求解问题(解的多元化)
3开关灯(开关门)问题(简化代码版)
科学记数法
在科学记数法中,一个数被写成一个1与10之间的实数(尾数)与一个10的幂的积,为了得到统一的表达方式,该尾数并不包括10:
782300=7.823×10^5
0.00012=1.2×10^(−4)
10000=1×10^4
在电脑或计算器中一般用E或e(英语Exponential)来表示10的幂:
7.823E5=782300
1.2e−4=0.00012
若用一般的方法,将一个数的所有数位都写出,在表示非常大或非常小的数时,将难以清楚知道它的大小,有时亦会浪费很多空间。使用科学记数法写的数的数量级、精确度和数值都非常明确。
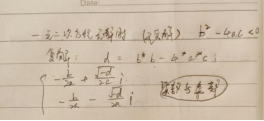
一元二次方程求解:
#include <cmath>
#include<iostream>
using namespace std;
int main()
{
double a, b, c, d, x1, x2, rp, ip ;
cin >> a >> b >> c ;
if ( fabs( a ) <= 1e-8 )
cout << " It is not quadratic." << endl ;
else
{
d = b * b - 4 * a * c ;
if ( fabs( d ) <= 1e-8 )
cout << "It has two equal real roots: " << -b / ( 2*a ) << endl ;
else
if ( d > 1e-8 )
{
x1 = ( -b + sqrt( d ) ) / ( 2*a ) ; x2 = ( -b - sqrt( d ) ) / ( 2*a ) ;
cout <<"It has two distinct real roots: "<<x1<<" and "<<x2<<endl ;
}
else
{
rp = -b / ( 2*a ) ; ip = sqrt( -d ) / ( 2*a ) ;
cout << "It has two complex roots: " << endl ;
cout << rp << " + " << ip << "i" << endl ;
cout << rp << " - " << ip << "i" << endl ;
}
}
return 0;
}
解此题时要注意解的个数,第一次判断是否为一元二次方程,当方程确定后判断解的个数,有两个相等的实根或不同的实根,最后也是关键部分,一般考虑不到,就是存在复解的情形。之前做题时当bb-4a*c<0时一般就判定无解(无实根),但是那仅局限于初中水平的数学。现在还要考虑到复解问题,这样情况才算完整。
灯
有 n 盏灯,编号为 1-n。第 1 个人把所数的开关(这些灯将被关掉),第 3 个掉的灯将被打开,开着的灯将被关闭)灯开着?输入第一行输入一个正整数 T (T<=10)接下来 T 行,每行输入一个正整数 n输出对于每个 n,输出 n 次操作后亮着的灯
样例
input
4
1
2
3
4
Output
1
1
1
2
对于这个题目让我想到了开关门问题:
当时是定义了内外双层循环:
int n,first=1;
memset(a,0sizeof(a));
for(int i=1;i<=n;i++);
for(int j=1;j<=n;j++);
if(j%i==0)a[j]!=a[j];
for(int i=1;i<=n;i++)
if(a[i])
{ if(first)first=0;else printf(“ “);
cout<<i;
}
这是当时100扇门的处理方法,输出开着的门,当然以上mesmet(a,0,sizeof(a))的作用是把数组a清零,它在cstrinig中定义。另外值得注意的是first的使用使得输出时除第一个变量前均有空格。不过好像又可以直接来打cout<<i<<” “;来实现,这种是最后不要求不留空格的情况下可以使用,当然也可以用for循环打到n-1,最后再打n,这种与题目做法是等效思想,但是在本题中行不通。
当然灯的问题中只要求输出个数,故最后只需要累加即可,然后n盏灯是否熄灭,多少盏灯还亮着就知道了,最后再从外围来一个大循环就可以计算T组数据了,但是缺点就是n太大时,每次内循环都要试n*n次,工作量太大。在此题中行不通,n 太大必然超时。
然后就引入了新的解法:
很容易考虑到因子个数上,偶数个因子的灯是关闭的,奇数个因子的灯是开着的(因为每个人都对他的倍数的灯做开关操作,因此当灯的因子确定后,每个因子的人对它进行一次相反操作,一开始灯都是关的,因此重复偶数次依然是关的,奇数次自然就是开的),而只有完全平方数的因子个数是奇数个。
对于一个数 x,可以看成因子是成对拆分出的,
例如:12=112=34,
而完全平方数存在 x=aa 的情况,
例如:36=136=218=312=49=66,对于 6*6,两数相同,算一个因子,所以完全平方数的因子个数是奇数个。
问题转化成,1-n 内有几个完全平方数,sqrt(n)个。
代码就可以简化为:
#include<bits/stdc++.h>
using namespace std;
int T;
int main()
{
long long n;
cin>>T;
while(T--)
{
cin>>n;
cout<<(int)(sqrt(n))<<endl;
}
}