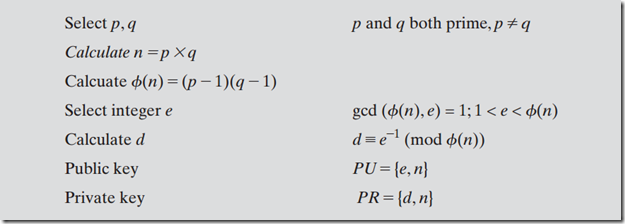RSA是一种非对称加密算法,在公开密钥和电子商业中RSA被广泛使用。它是基于一个很简单的数论事实,两个素数相乘很容易,对两素数乘积因式分解很困难。原理就不再阐述了,我谈谈算法的编程实现过程。
一、RSA加密和解密过程是基于以下形式,其中明文为M,密文为C,公匙PU={e, n},密匙PR={d, n}。
1、准备工作,选择两个大素数p和q,计算p和q的乘积n,计算p-1和q-1的乘积,选择一个与p-1和q-1乘积互质的数e,计算出d
2、加密过程
3、解密过程
程序没有生成大素数,只是列出1000以内的素数,随机取两个素数p和q,利用欧德里德扩展算法计算出e和d,用反复平方法求数的幂
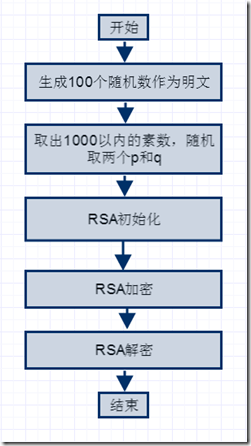
二、程序流程图
三、程序源码
 View Code1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <ctime> 5 #include <cstdlib> 6 using namespace std; 7 8 9 int Plaintext[100];//明文 10 long long Ciphertext[100];//密文 11 int n, e = 0, d; 12 13 //二进制转换 14 int BianaryTransform(int num, int bin_num[]) 15 { 16 17 int i = 0, mod = 0; 18 19 //转换为二进制,逆向暂存temp[]数组中 20 while(num != 0) 21 { 22 mod = num%2; 23 bin_num[i] = mod; 24 num = num/2; 25 i++; 26 } 27 28 //返回二进制数的位数 29 return i; 30 } 31 32 //反复平方求幂 33 long long Modular_Exonentiation(long long a, int b, int n) 34 { 35 int c = 0, bin_num[1000]; 36 long long d = 1; 37 int k = BianaryTransform(b, bin_num)-1; 38 39 for(int i = k; i >= 0; i--) 40 { 41 c = 2*c; 42 d = (d*d)%n; 43 if(bin_num[i] == 1) 44 { 45 c = c + 1; 46 d = (d*a)%n; 47 } 48 } 49 return d; 50 } 51 52 //生成1000以内素数 53 int ProducePrimeNumber(int prime[]) 54 { 55 int c = 0, vis[1001]; 56 memset(vis, 0, sizeof(vis)); 57 for(int i = 2; i <= 1000; i++)if(!vis[i]) 58 { 59 prime[c++] = i; 60 for(int j = i*i; j <= 1000; j+=i) 61 vis[j] = 1; 62 } 63 64 return c; 65 } 66 67 68 //欧几里得扩展算法 69 int Exgcd(int m,int n,int &x) 70 { 71 int x1,y1,x0,y0, y; 72 x0=1; y0=0; 73 x1=0; y1=1; 74 x=0; y=1; 75 int r=m%n; 76 int q=(m-r)/n; 77 while(r) 78 { 79 x=x0-q*x1; y=y0-q*y1; 80 x0=x1; y0=y1; 81 x1=x; y1=y; 82 m=n; n=r; r=m%n; 83 q=(m-r)/n; 84 } 85 return n; 86 } 87 88 //RSA初始化 89 void RSA_Initialize() 90 { 91 //取出1000内素数保存在prime[]数组中 92 int prime[5000]; 93 int count_Prime = ProducePrimeNumber(prime); 94 95 //随机取两个素数p,q 96 srand((unsigned)time(NULL)); 97 int ranNum1 = rand()%count_Prime; 98 int ranNum2 = rand()%count_Prime; 99 int p = prime[ranNum1], q = prime[ranNum2]; 100 101 n = p*q; 102 103 int On = (p-1)*(q-1); 104 105 106 //用欧几里德扩展算法求e,d 107 for(int j = 3; j < On; j+=1331) 108 { 109 int gcd = Exgcd(j, On, d); 110 if( gcd == 1 && d > 0) 111 { 112 e = j; 113 break; 114 } 115 116 } 117 118 } 119 120 //RSA加密 121 void RSA_Encrypt() 122 { 123 cout<<"Public Key (e, n) : e = "<<e<<" n = "<<n<<' '; 124 cout<<"Private Key (d, n) : d = "<<d<<" n = "<<n<<' '<<' '; 125 126 int i = 0; 127 for(i = 0; i < 100; i++) 128 Ciphertext[i] = Modular_Exonentiation(Plaintext[i], e, n); 129 130 cout<<"Use the public key (e, n) to encrypt:"<<' '; 131 for(i = 0; i < 100; i++) 132 cout<<Ciphertext[i]<<" "; 133 cout<<' '<<' '; 134 } 135 136 //RSA解密 137 void RSA_Decrypt() 138 { 139 int i = 0; 140 for(i = 0; i < 100; i++) 141 Ciphertext[i] = Modular_Exonentiation(Ciphertext[i], d, n); 142 143 cout<<"Use private key (d, n) to decrypt:"<<' '; 144 for(i = 0; i < 100; i++) 145 cout<<Ciphertext[i]<<" "; 146 cout<<' '<<' '; 147 } 148 149 150 //算法初始化 151 void Initialize() 152 { 153 int i; 154 srand((unsigned)time(NULL)); 155 for(i = 0; i < 100; i++) 156 Plaintext[i] = rand()%1000; 157 158 cout<<"Generate 100 random numbers:"<<' '; 159 for(i = 0; i < 100; i++) 160 cout<<Plaintext[i]<<" "; 161 cout<<' '<<' '; 162 } 163 164 int main() 165 { 166 Initialize(); 167 168 while(!e) 169 RSA_Initialize(); 170 171 RSA_Encrypt(); 172 173 RSA_Decrypt(); 174 175 return 0; 176 }
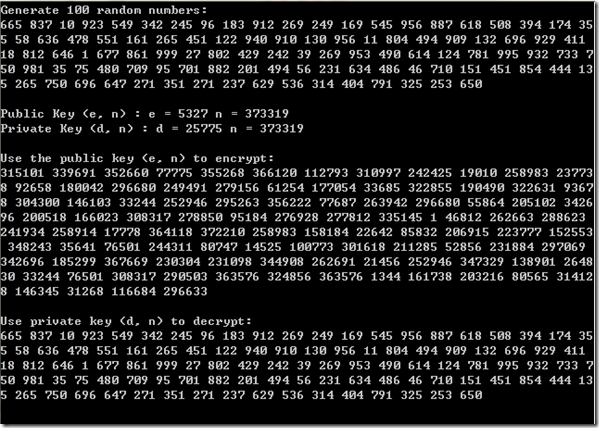
View Code1 #include <iostream> 2 #include <cmath> 3 #include <cstring> 4 #include <ctime> 5 #include <cstdlib> 6 using namespace std; 7 8 9 int Plaintext[100];//明文 10 long long Ciphertext[100];//密文 11 int n, e = 0, d; 12 13 //二进制转换 14 int BianaryTransform(int num, int bin_num[]) 15 { 16 17 int i = 0, mod = 0; 18 19 //转换为二进制,逆向暂存temp[]数组中 20 while(num != 0) 21 { 22 mod = num%2; 23 bin_num[i] = mod; 24 num = num/2; 25 i++; 26 } 27 28 //返回二进制数的位数 29 return i; 30 } 31 32 //反复平方求幂 33 long long Modular_Exonentiation(long long a, int b, int n) 34 { 35 int c = 0, bin_num[1000]; 36 long long d = 1; 37 int k = BianaryTransform(b, bin_num)-1; 38 39 for(int i = k; i >= 0; i--) 40 { 41 c = 2*c; 42 d = (d*d)%n; 43 if(bin_num[i] == 1) 44 { 45 c = c + 1; 46 d = (d*a)%n; 47 } 48 } 49 return d; 50 } 51 52 //生成1000以内素数 53 int ProducePrimeNumber(int prime[]) 54 { 55 int c = 0, vis[1001]; 56 memset(vis, 0, sizeof(vis)); 57 for(int i = 2; i <= 1000; i++)if(!vis[i]) 58 { 59 prime[c++] = i; 60 for(int j = i*i; j <= 1000; j+=i) 61 vis[j] = 1; 62 } 63 64 return c; 65 } 66 67 68 //欧几里得扩展算法 69 int Exgcd(int m,int n,int &x) 70 { 71 int x1,y1,x0,y0, y; 72 x0=1; y0=0; 73 x1=0; y1=1; 74 x=0; y=1; 75 int r=m%n; 76 int q=(m-r)/n; 77 while(r) 78 { 79 x=x0-q*x1; y=y0-q*y1; 80 x0=x1; y0=y1; 81 x1=x; y1=y; 82 m=n; n=r; r=m%n; 83 q=(m-r)/n; 84 } 85 return n; 86 } 87 88 //RSA初始化 89 void RSA_Initialize() 90 { 91 //取出1000内素数保存在prime[]数组中 92 int prime[5000]; 93 int count_Prime = ProducePrimeNumber(prime); 94 95 //随机取两个素数p,q 96 srand((unsigned)time(NULL)); 97 int ranNum1 = rand()%count_Prime; 98 int ranNum2 = rand()%count_Prime; 99 int p = prime[ranNum1], q = prime[ranNum2]; 100 101 n = p*q; 102 103 int On = (p-1)*(q-1); 104 105 106 //用欧几里德扩展算法求e,d 107 for(int j = 3; j < On; j+=1331) 108 { 109 int gcd = Exgcd(j, On, d); 110 if( gcd == 1 && d > 0) 111 { 112 e = j; 113 break; 114 } 115 116 } 117 118 } 119 120 //RSA加密 121 void RSA_Encrypt() 122 { 123 cout<<"Public Key (e, n) : e = "<<e<<" n = "<<n<<' '; 124 cout<<"Private Key (d, n) : d = "<<d<<" n = "<<n<<' '<<' '; 125 126 int i = 0; 127 for(i = 0; i < 100; i++) 128 Ciphertext[i] = Modular_Exonentiation(Plaintext[i], e, n); 129 130 cout<<"Use the public key (e, n) to encrypt:"<<' '; 131 for(i = 0; i < 100; i++) 132 cout<<Ciphertext[i]<<" "; 133 cout<<' '<<' '; 134 } 135 136 //RSA解密 137 void RSA_Decrypt() 138 { 139 int i = 0; 140 for(i = 0; i < 100; i++) 141 Ciphertext[i] = Modular_Exonentiation(Ciphertext[i], d, n); 142 143 cout<<"Use private key (d, n) to decrypt:"<<' '; 144 for(i = 0; i < 100; i++) 145 cout<<Ciphertext[i]<<" "; 146 cout<<' '<<' '; 147 } 148 149 150 //算法初始化 151 void Initialize() 152 { 153 int i; 154 srand((unsigned)time(NULL)); 155 for(i = 0; i < 100; i++) 156 Plaintext[i] = rand()%1000; 157 158 cout<<"Generate 100 random numbers:"<<' '; 159 for(i = 0; i < 100; i++) 160 cout<<Plaintext[i]<<" "; 161 cout<<' '<<' '; 162 } 163 164 int main() 165 { 166 Initialize(); 167 168 while(!e) 169 RSA_Initialize(); 170 171 RSA_Encrypt(); 172 173 RSA_Decrypt(); 174 175 return 0; 176 }四、运行结果