% 等高线矩阵的获取
C = contourc(peaks(20),3); % 获取3个等级的等高线矩阵
% 等高线图形的绘制
contour(peaks(20),10);colormap autumn % 绘制二维的等高线
contour3(peaks(20),10);colormap autumn % 绘制三维的等高线
% 还可以指定等高线的条数、坐标系的比例及某高度上的等高线
% 等高线图形的填充
contourf(peaks(20),10);colormap autumn %绘制填充的二维等高线,有n的等级
%等高线图形的标注
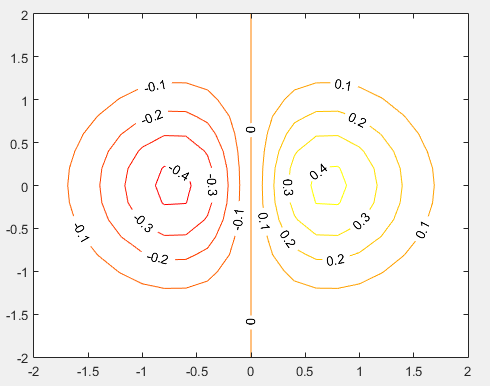
[x,y]=meshgrid(-2:.2:2);%生成格网
z=x.^exp(-x.^2-y.^2); %函数
[C,h]=contour(x,y,z);colormap autumn;
%-----方法一
text_handle = clabel(C,h);
set(text_handle,'BackgroundColor',[1 1 .6],'Edgecolor',[.7 .7 .7])
%标注颜色设置为黄色 %标注的“边界”设置为灰色
%-----方法二
clabel(C,h,'FontSize',10,'Color','r','LabelSpacing',72,'Rotation',0);
%字体大小 %颜色 %两个标注的间隔 %标注(字)是否旋转
——more information see matlab帮助——Contour Plots
等高线矩阵的数据结构
[C,h]=contour(x,y,z);colormap autumn;
% C是等高线矩阵,包括x,y坐标和该点等高线的等级
% C的记录格式如下图
| height1 | x1 | …… | xN1 | height2 | …… |
| 点数N1 | y1 | …… | yN1 | 点数N2 | …… |
注2:当等高线被边界截断时,等高线是不闭合的;闭合的等高线第一个点与最后一个点相等。
注3:h.ContourMatrix同样可以获取该等高线矩阵
如何只计算等高线矩阵
% 数据准备
[x,y]=meshgrid(-2:.2:2); %生成格网
z=x.*exp(-x.^2-y.^2); %函数
% 获取height=k的等高线上的各点坐标
k = 0.2;
C = contourc(-2:.2:2,-2:.2:2,z,[k,k]);
% 获取height=k的‘各’等高线上的各点坐标
k = [0,0.1,0.2,0.3,0.4];
C = contourc(-2:.2:2,-2:.2:2,z,k);
% 获取n条等间距等高线上的各点坐标
n = 3;
C = contourc(-2:.2:2,-2:.2:2,z,3);
<wiz_tmp_tag id="wiz-table-range-border" contenteditable="false" style="display: none;">