1. 二叉树的自相似性
|
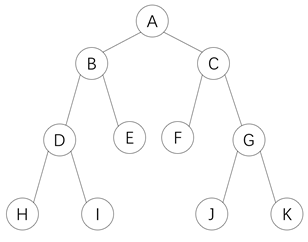
1、首先给出一个普通二叉树的结构图 |
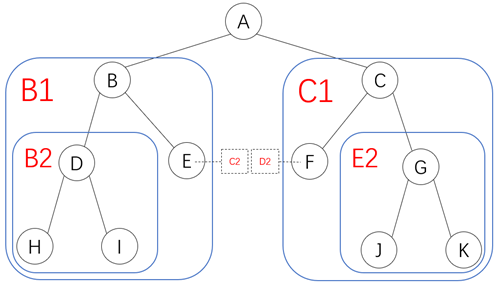
2、然后对其进行一个分解 |
|
|
|
这里将最小二叉树H-D-I当做一个结点B2,J-G-K当做一个结点E2。那么B2-B-E(B2-B-C2)就可以当做一个最小二叉树,将这个整体当做一个结点记为B1,F-C-E2(D2-C-E2)就可以当做一个最小二叉树,将这个整体当做一个结点记为C1。所以B1-A-C1也是一个最小二叉树。
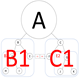
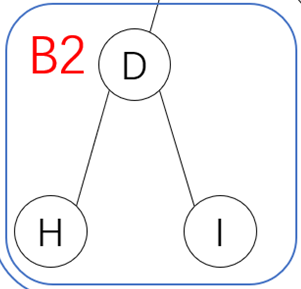
如果在图形上将根节点放大,如下图左1。然后将整个图像缩小,如下图左2。那么做2就几乎只能看到由结点B1-A-C1组成的最小二叉树。如果将整个图像放大到B2,并且只聚焦到B2,如下图右1,则可以看出它也是一个最小二叉树。这与分形几何上所讲的自相似性很一致。
|
|
|
|
2. 用自相似的思想来理解二叉树的三种遍历方法
三种遍历方法无非就是先序(根左右),中序(左根右),后序(左右根)。
首先将整体看成一个最小二叉树B1-A-C1。然后分别讲一下这三种方法的遍历顺序
2.1. 先序遍历
最小二叉树B1-A-C1的先序遍历顺序就是A, B1, C1
因为B1,C1都不是最小的节点,分别对其按先序遍历的顺序展开可得:A, (B, B2, E), (C, F, E2)
由于B2,E2也不是最小的节点,再次对其按先序遍历的顺序展开可得:A, (B, (D, H, I), E), (C, F, (J, G, K))
整理可得:A, B, D, H, I, E, C, F, J, G, K.
2.2. 中序遍历
最小二叉树B1-A-C1的中序遍历顺序就是B1, A, C1
因为B1,C1都不是最小的节点,分别对其按中序遍历的顺序展开可得:(B2, B, E), A, (F, C, E2)
由于B2,E2也不是最小的节点,再次对其按中序遍历的顺序展开可得:((H, D, I), B, E), A, (F, C, (J, G, K))
整理可得:H, D, I, B, E, A, F, C, J, G, K.
2.3. 后序遍历
最小二叉树B1-A-C1的后序遍历顺序就是B1, C1, A
因为B1,C1都不是最小的节点,分别将其展开可得:(B2, E, B), (F, E2, C), A
由于B2,E2也不是最小的节点,再次对其展开可得:((H, I, D), E, B), (F, (J, K, G), C), A
整理可得:H, I, D, E, B, F, J, K, G, C, A.
2.4. 总结
其实这三种遍历方法都暗含了递归的思想。
所谓先、中、后无非就是先固定了左右的位置,然后根据根节点相对于"左右"的位置来判断;如果在最前面就是"根左右",即先序遍历。
如果用图表示的话,三种遍历顺序组成的箭头可以看成是自相似的漩涡。这里就不赘述了。