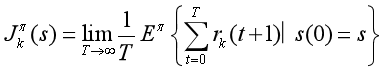一、引言
- 多智能体强化学习的标准模型：
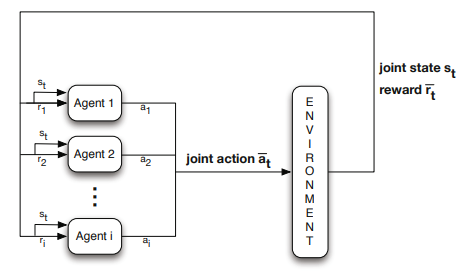
多智能体产生动作a1，a2.....an联合作用于环境，环境返回当前的状态st和奖励rt。智能体接受到系统的反馈st和ri，根据反馈信息选择下一步的策略。
二、重复博弈
- 正规形式博弈
- 定义：正规形式的博弈是一个元组(n,A1,...,n,R1,...,n)
n代表n个参与者
Ak代表参与者k能够选择的动作
Rk是参与者k的奖励函数，指定他通过执行动作a∈A1×A2....×An
-纯策略与混合策略：如果动作a ∈ Ak，且σk(a) = 1，而其他所有动作σall-k(a) = 0，则称为全策略。否则称为混合策略。
-
玩家k在策略配置σ下的预期回报：
-
经典的双人博弈：(a)匹配硬币，一种纯粹的竞争(零和)游戏。(b)囚徒困境，一般和博弈。(c)协调博弈，即共同利益(相同收益)博弈。(d)性别博弈，各主体偏好不同的协调博弈)纯纳什均衡用粗体表示。
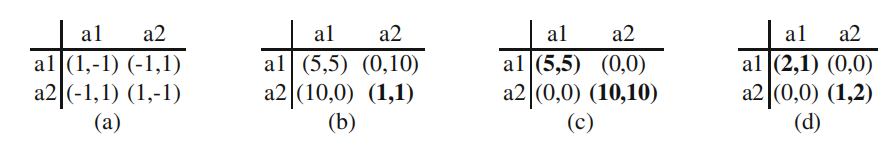
博弈a：玩家1和玩家2一起抛硬币，若是双方硬币是同一面的，则玩家1获胜，否则玩家2获胜。零和博弈
博弈b：囚徒博弈，一般和博弈。
博弈c：一个共同兴趣游戏。在这种情况下，两个玩家在每次联合行动中获得相同的收益。这个游戏的挑战是让玩家协调最优的联合行动。选择错误的联合行动将给出次优收益，而未能协调结果将得到0收益。
博弈d：性别之战，是另一个协调游戏的例子。然而，在这里，玩家会获得个人奖励，并偏好不同的结果。Agent 1偏好(a1,a1)而Agent 2偏好(a2,a2)除了协调问题之外，玩家现在还必须就哪种优选结果达成一致。 -
3个动作的共同兴趣游戏：(a)攀爬对策(b)惩罚对策，k≤0。这两款游戏都具有共同的兴趣类型。纯纳什均衡用粗体表示。
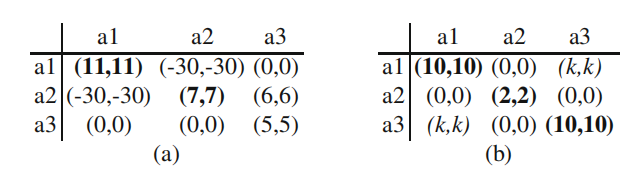
- 博弈中的解决方案概念
-
定义：设σ = (σ1,…,σn)是一个策略配置，令
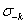表示相同的策略配置，但不包含参与人k的策略σk。如果下列条件成立，则
称为参与人k的最佳响应:
-
纳什均衡的定义：（纳什均衡是博弈的核心解决概念）
如果对于每个玩家k，策略σk是对其他玩家σ−k的策略的最佳响应，则策略轮廓σ=(σ1，...，σn)被称为纳什均衡。
- 重复博弈中的强化学习
-
遗憾值定义：
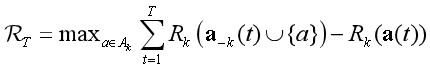
其中a(t)表示在t时玩的联合动作，a−k(t)∪{a}表示相同的联合动作，但玩家k选择动作a。 -
梯度上升方法
线性奖励-处罚：
r(t)为时刻t接收到的反馈，K为自动机可用的动作数。λ1 和λ2 是常数，分别称为奖励和惩罚参数。根据这些参数的值，可以考虑算法的3种不同的变化。当λ1 =λ2，该算法被称为线性奖罚(LR−P)，而当λ1 > >λ2时，称为线性奖励-ε惩罚(LR−εP)。．如果λ2 = 0的算法被称为线性奖励-不作为(LR−I)．
顺序博弈
- 马尔可夫场
- 定义：马尔可夫对策是一个元组(n,S,A1,...,n, R1,...,nT):
n 系统中智能体的个数
S 系统状态的有限集合
Ak 智能体k的动作集合
Rk 智能体k的奖励函数
T 转移函数
在联合策略下π = (π1,π…n)，agent k的期望折扣报酬的定义如下：
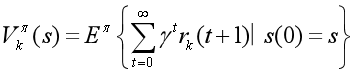
该策略为每一个代理i分配了一个策略πi
而该联合策略下agent k的平均报酬定义为:
