2018-06-11一:
首先来一个简单明了的简介。。。
Binary Search Tree 即BST,又称二叉排序树,二叉查找树。
二叉搜索树的名字是怎么来的呢?很简单,因为这棵树有那么一个特性:所有节点的儿子最多只有两个:左儿子和右儿子。
而这父子节点之间又满足如下3条关系:(对于一个父节点)
1.若有左子树,那么左子树上面的所有点的权值都小于父节点的权值。
2.若有右子树,那么右子树上面的所有点的权值都大于父节点的权值。
3.子树均为二叉搜索树。(即满足上面的所有特性)
嗯,所以根据上方的定义,我们可以得出这么一个结论:
左子树节点值<根节点值<右子树节点值。也就是说二叉搜索树的中序遍历是递增的。
下面就是一个满足二叉搜索树性质的树。
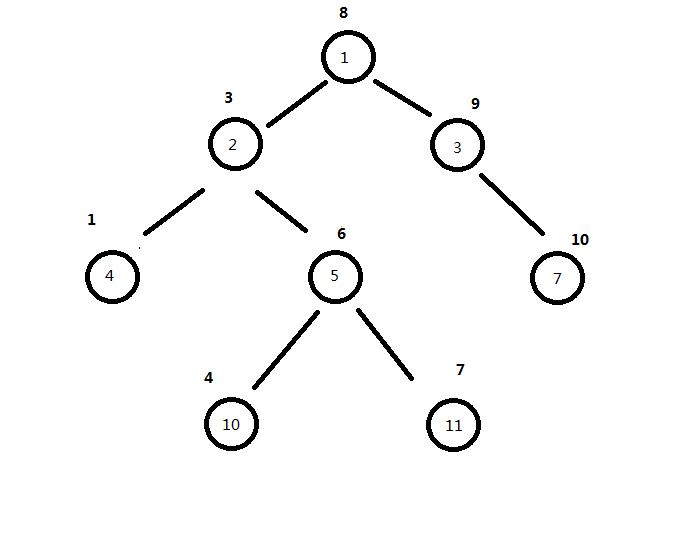
圈内是编号,圈外是权值,我们可以很清楚的发现,对弈从1~8的每一个几点做父节点,都满足上述的三个关系。
然后,我们还发现,每一个节点的左儿子的编号是其两倍,每一个节点的右儿子编号是其二倍+1;
二:
根据名称我们就可以知道:二叉搜索树的作用主要在搜索和查找。那么对于整个查找的过程又是怎么样实现的呢?
1.查找值为x的节点的编号。
那么伪代码如下:
//查找值为x的节点的编号 if(树为空)//即root==NULL return ; else search(1,x); int search(int x,int now) //查找到了now节点 { if(now节点的值==x) 查找成功,return now; if(now节点的值<x) search(x,右子树); else if(now节点的值>x) seach(x,左子树); }
根据上文二叉搜索树的性质来看,如果要查询的节点比当前节点的权值要小,那么他就一定在当前节点的左子树上,反之,如果比当前节点的权值要打,那么他就一定在其右子树上面。
这样的查找其实就是一个递归实现的过程,复杂度大概在O(logn)。
我们定义一个value[i]代表i节点的值,(这里用了结构体)那么代码大概就是这样:
#define MAXN 100010 struct point {
int sub//子树大小 int left_son;//左儿子 int right_son;//右儿子 int value;//权值
int sum;//跟该节点相同权值的节点个数,因为二叉搜索树中不能有相同权值的节点。
int father//父亲节点
}edge[MAXN]; int search(int x,int now) { if(x==edge[now].value) return now; if(x>edge[now].value) search(x,edge[now].right_son); if(x<edge[now].value) search(x,edge[now].left_son); }
2.查找最小值
因为二叉搜索树的性质就是左子树节点值<根节点值<右子树节点值。所以我们就从根节点开始一直朝左子树走就好了。
int seach_min(int now) { if(edge[now].left_son)//如果还有左儿子的话 search_min(edge[now].left_son);//继续搜索左儿子 else return now; //否则返回当前节点 }
3.查找最大值
和最小值一个道理,从根节点开始一直朝右子树走就好,直到走到没有右儿子,那么就返回当前节点。
int search_max(int now) { if(edge[now].right_son) search_max(edge[now].right_son); else return now; }
4.插入一个权值为x的节点。
对于这个操作,首先要判断:该树是不是个空树。那么在这里我们定义一个root一直指向二叉搜索树的根节点,那么要判断这棵树是不是为空,我们只需要判断root是不是指向NULL就可以了。
然后接下来还有一个在递归中的判断,就是我们if一下当前节点的值是不是等于要插入的节点的值,如果是的话,我们就不进行插入,直接将该节点的sum++就可以了。
然后,就是可以插入的情况。我们先把该节点指向根节点,然后不断的进行递归维护二叉搜索树性质就可以了。
void insert(int x,int now) { if(root==NULL)//如果是个空树 root=x;//直接将根节点设为x就可以了。 if(edge[now].value==x)//如果树中已经有该值的节点 { edge[now].sum++;//将该节点的sum++; return ;//返回false就好。 } if(edge[now].value<x)//如果当前节点的权值小于x if(edge[now].right_son)//如果当前节点有右儿子 insert(x,edge[now].right_son);//递归其右子树 else//如果没有 { edge[now].right_son=now*2+1;//新增右儿子 edge[edge[now].right_son].value=x;//给右儿子赋值 return ; } if(edge[now].value>x)//如果当前节点的权值大于x if(edge[now].left_son)//如果当前节点有左儿子 insert(x,edge[now].left_son);//递归其左子树 else//如果没有 { edge[now].left_son=now*2;//新增左儿子 edge[edge[now].left_son].value=x;//给左儿子赋值 return ; } }
5.删除编号为x的节点。
我们在删除这里要注意的事项非常多,第一:要有很多的判别。
在诸多判别之前,我们还要先判断一个:就是当前节点是不是根节点,如果是的话,我们将root指向当前节点的左孩子或者右孩子,然后clear根节点的所有属性,返回true。
one:如果当前要删除的节点是一个叶子节点,那么直接删除就好了。
two:如果只有左儿子:我们就让这个节点的父亲的左儿子指向这个节点的左儿子,然后clear这个节点的所有属性。返回true
three:如果只有右儿子:我们就让这个节点的父亲的右儿子指向这个节点的右儿子,然后clear这个节点的所有属性。返回true
four:如果有左右两个儿子:这个是最最麻烦的,我们首先要找到该节点的右子树的最左边的孩子,把他的值和要删除的节点的值交换,然后删除这个孩子,然后返回true。
图示差不多是这样的:
1.如果说我们要删除11号节点,然后我们发下它既没有右儿子,也没有左儿子,那么我们直接清除这个节点的所有属性就好了。
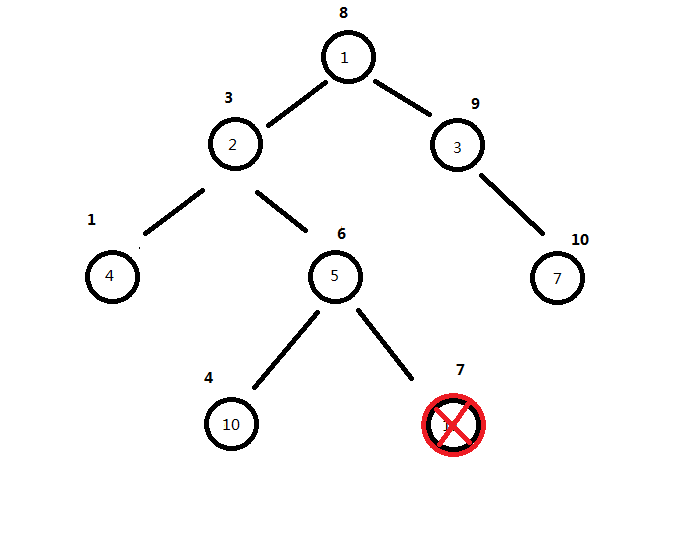
2.比如说我们现在要删除3节点,然后我们发现他只有7节点一个右儿子
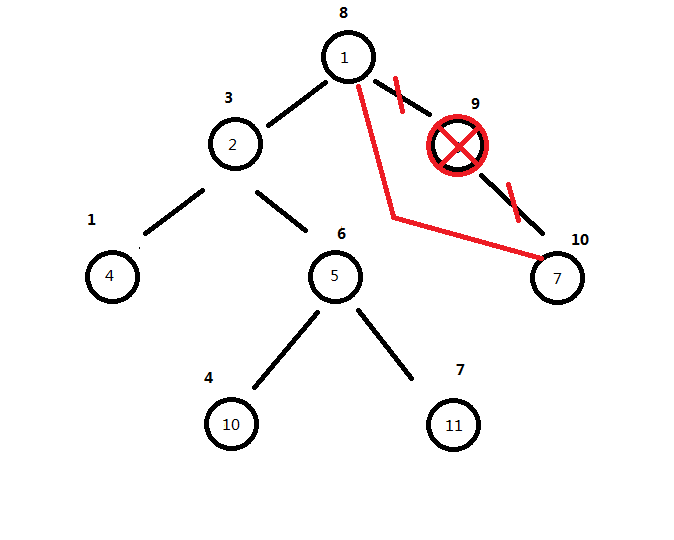
很清楚了,我们就是3节点的右儿子改成他爷爷的右儿子,就是相当于篡位,然后我们clear3节点的所有属性就可以了。
然后如果只有左儿子也是一样的。
接下来就是最麻烦的最后一种情况了,比如说我们现在要删除2节点,然后我们发现它既有左儿子,又有右儿子。
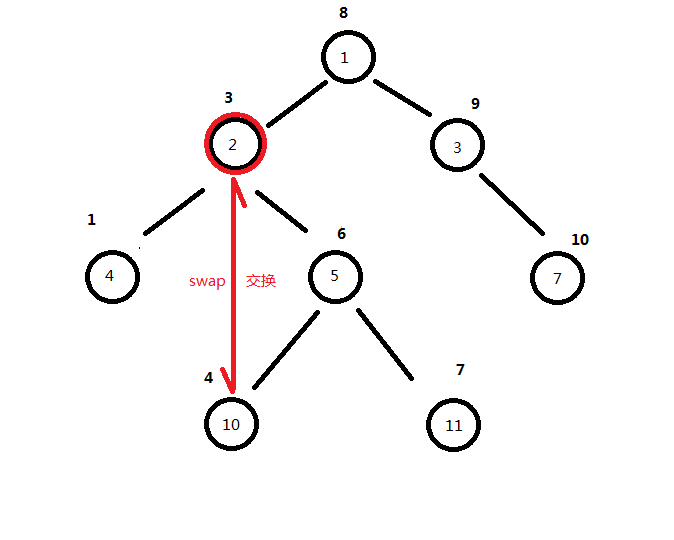
我们首先找到2节点的右子树中的最左边的节点,然后进行交换。

最后我们删除交换后的2节点就可以了。
代码差不多是这个样子的:
void _delete(int x) { if(root==x)//如果要删除的节点是根节点。 root=edge[x].leftson;//找个儿子提上去。 if(!edge[x].left_son)//如果既没有左儿子 if(!edge[x].right_son)//也没有右儿子 { All_clear(x);//直接删除就好了。 return ; } if(edge[x].left_son)//如果只有左儿子 if(!edge[x].right_son)//没有右儿子 { edge[edge[x].father].left_son=edge[x].left_son; //把x的父亲的左儿子置为x的左儿子 All_clear(x);//清空x。 return ; } if(edge[x].right_son)//如果只有右儿子 if(!edge[x].left_son)//没有左儿子 { edge[edge[x].father].right_son=edge[x].right_son; //把x的父亲的右儿子置为x的右儿子 All_chear(x);//清空x return ; } if(edge[x].left_son)//如果既有左儿子 if(edge[x].right_son)//又有右儿子 { int rs=edge[x].right_son;//设置右儿子 int mrs=rs; while(edge[rs].left_son)//如果还有左儿子 mrs=edge[rs].left_son;//更新为左儿子 //上述步骤就是找x的右子树上面的最左边的儿子 swap(edge[x].value,edge[mrs].value);//交换其值。 All_clear(mrs);//直接清空mrs. return ; } }
5.emm,还有最后一个(排版不大好呢qnq):查询一个排名为k的数
这个的思路就不再多讲了,直接上代码好了(绝不是because Yeasion懒哦......
int find(int x,int now) { int now=root; while(1) { if(edge[now].left_son&&x<=edge[edge[now].left_son].sub) now=edge[now].left_son; else { int temp=(edge[now].left_son?edge[edge[now].left_son].sub:0)+edge[now].sum; if(x<=temp)return edge[now].value; x-=temp; now=edge[now].right_son; } } }
恩,最基本的BST差不多就是这样。
其实BST还支持很多很厉害的操作,像平衡树,线段树之类的,这里介绍的是最基本的BST的代码实现和概念,如果大家想练一练手的话可以去看看这个题:P3369 【模板】普通平衡树(Treap/SBT)
(代码全是现码的,可能有误~~qwq)
接下来是全部代码,由于Yeasion懒得再写一边了,在这里放上的有点splay。。其实都一样的,如果好好听了的话,应该能看懂的。
// luogu-judger-enable-o2 #include<cstdio> #include<iostream> #include<cstdlib> #include<ctime> using namespace std; struct node { int val; int yuk; int siz; int key; int ch[2]; }; node t[501000]; int tail; int cmp(int now,int val) { if(t[now].val==val) return -1; return t[now].val > val ? 0 : 1 ; } void sum(int &now) { t[now].siz=t[t[now].ch[0]].siz+t[t[now].ch[1]].siz+t[now].yuk; return ; } void rotato(int &now,int base) { int k=t[now].ch[base^1]; t[now].ch[base^1]=t[k].ch[base]; t[k].ch[base]=now; sum(now); sum(k); now=k; } int New(int val) { ++tail; t[tail].ch[0]=t[tail].ch[1]=0; t[tail].siz=1;t[tail].yuk=1; t[tail].val=val; t[tail].key=rand(); return tail; } void init() { t[0].val=0;t[0].yuk=0; t[0].key=-1; t[0].ch[0]=t[0].ch[1]=0; srand(time(NULL)); return ; } void insert(int &now,int val) { if(now==0){now=New(val);return ;} int dir=cmp(now,val); if(dir==-1){t[now].yuk+=1;t[now].siz+=1;return ;} insert(t[now].ch[dir],val); if(t[t[now].ch[dir]].key>t[now].key) rotato(now,dir^1); sum(now); } void del(int &now,int val) { int dir=cmp(now,val); if(dir==-1) if(t[now].yuk>1){t[now].siz-=1,t[now].yuk-=1;return;} else { if(t[now].ch[1]&&t[now].ch[0]) { int nxt= t[t[now].ch[0]].key > t[t[now].ch[1]].key ? 0 : 1; rotato(now,nxt^1); del(t[now].ch[nxt^1],val); sum(now);return ; } if(t[now].ch[1]){now=t[now].ch[1];sum(now);return ;} else {now=t[now].ch[0];sum(now);return ;} } del(t[now].ch[dir],val);sum(now); return; } int nxt(int now,int val) { if(!now) return 0x7fffffff; if(t[now].val>val) return min(t[now].val,nxt(t[now].ch[0],val)); else return nxt(t[now].ch[1],val); } int pre(int now,int val) { if(!now) return -0x7fffffff; if(t[now].val<val) return max(t[now].val,pre(t[now].ch[1],val)); else return pre(t[now].ch[0],val); } int find(int &now,int val) { int dir=cmp(now,val); if(dir==-1) return t[t[now].ch[0]].siz+1; return find(t[now].ch[dir],val) + ( dir ? t[t[now].ch[0]].siz + t[now].yuk : 0); } int kth(int &now,int k) { if(t[t[now].ch[0]].siz<k&&t[t[now].ch[0]].siz+t[now].yuk>=k) return t[now].val; if(k<=t[t[now].ch[0]].siz) return kth(t[now].ch[0],k); else return kth(t[now].ch[1],k-t[t[now].ch[0]].siz-t[now].yuk); } int root; void visit(int now) { if(!now) return ; visit(t[now].ch[0]); printf("%d ",t[now].val); visit(t[now].ch[1]); return ; } int main() { int n; scanf("%d",&n); int a,b; for(int i=1;i<=n;i++) { scanf("%d%d",&a,&b); switch(a) { case 1:insert(root,b);break; case 2:del(root,b);break; case 3:printf("%d ",find(root,b));break; case 4:printf("%d ",kth(root,b));break; case 5:insert(root,b);printf("%d ",pre(root,b));del(root,b);break; case 6:insert(root,b);printf("%d ",nxt(root,b));del(root,b);break; } //visit(root);printf(" "); } }
——Yeasion_Nein