看了这篇博客https://blog.csdn.net/u013520118/article/details/48032599
但是这篇里面没有写结论的证明, 我来证明一下。
首先结论是对于E图而言,如果存在i和j结点到k1都有边,而i和j中只有一个结点到k2有边,则这个图是不可能转化来的。
首先先讲E图中i和j结点到k1都有边, 那么图会是怎么样的呢?有三种情况
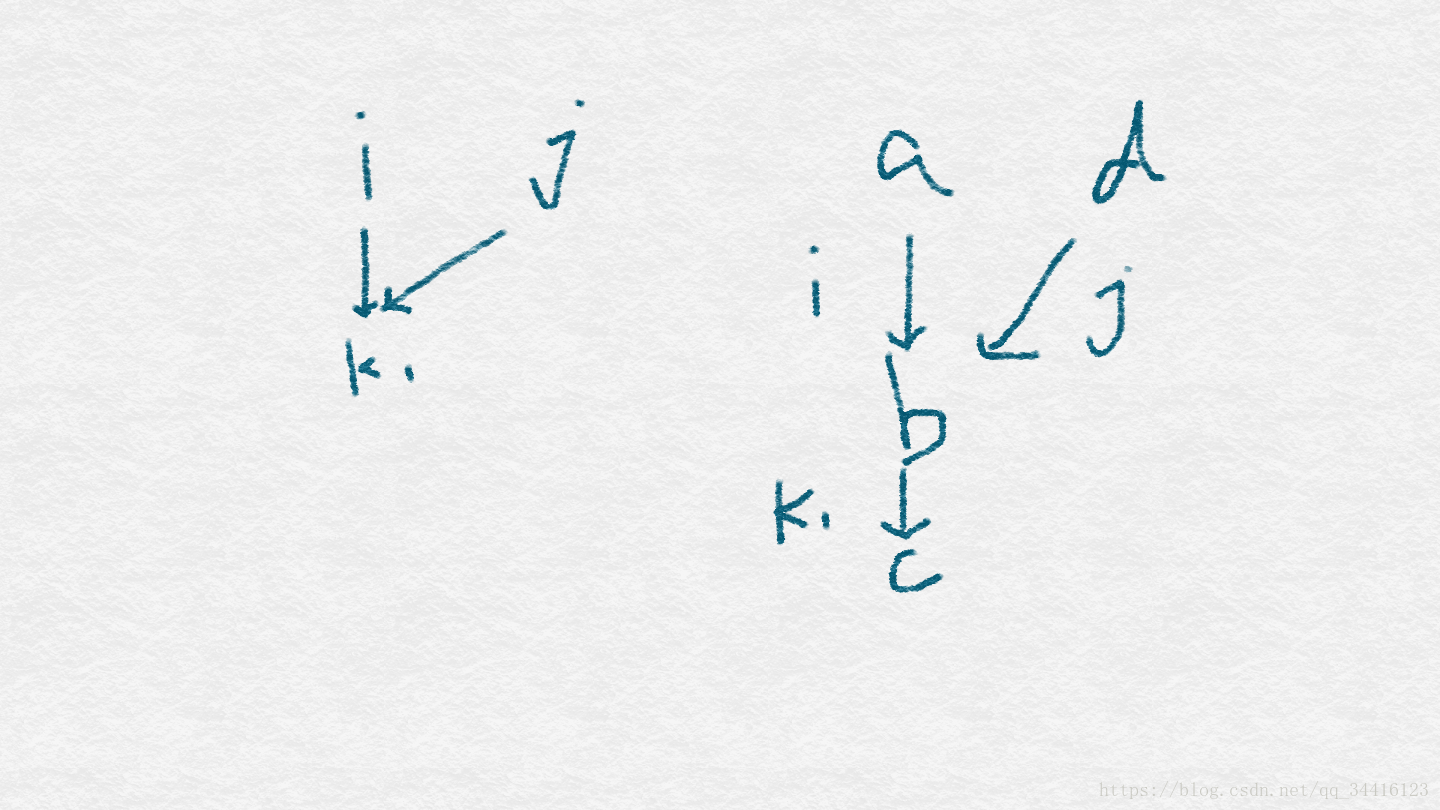
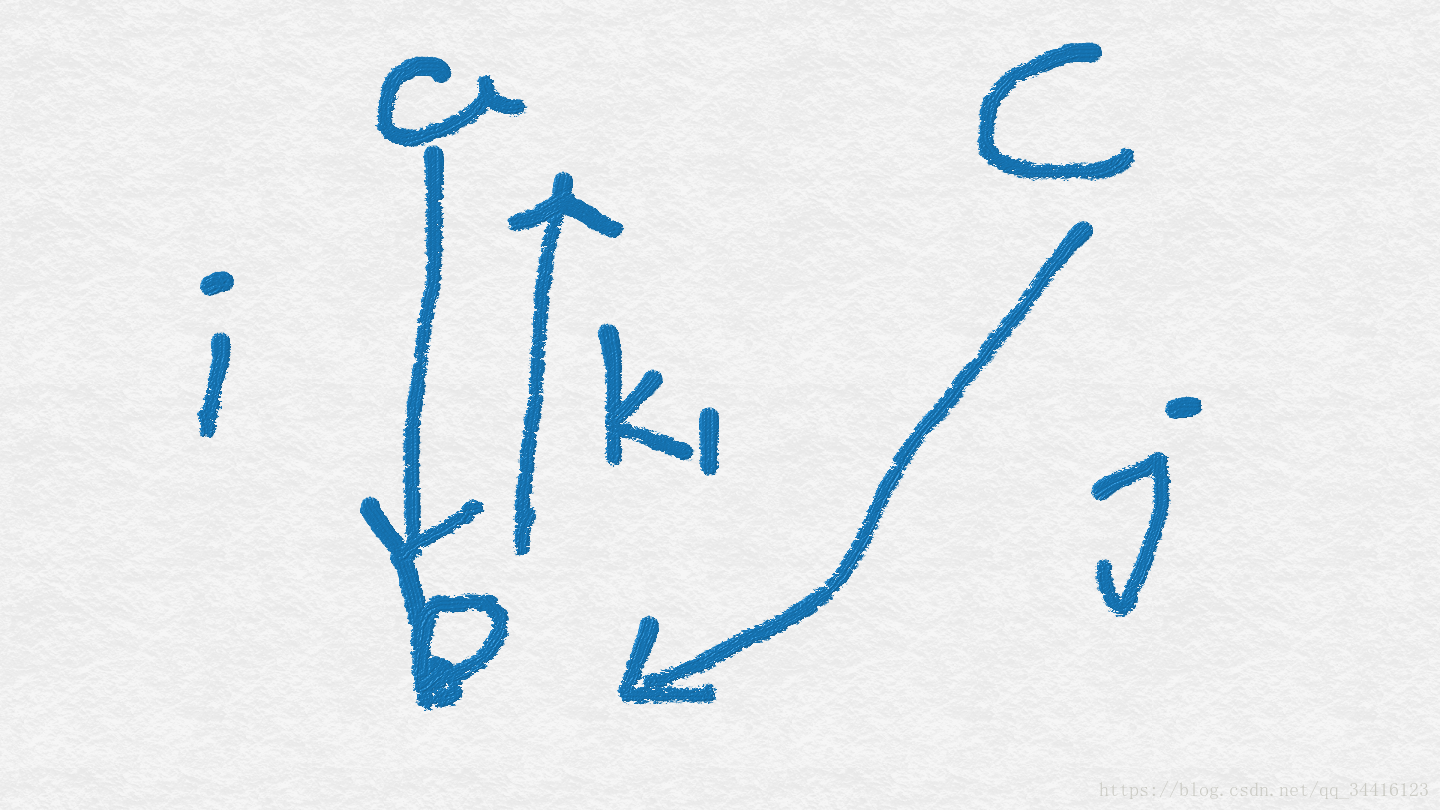
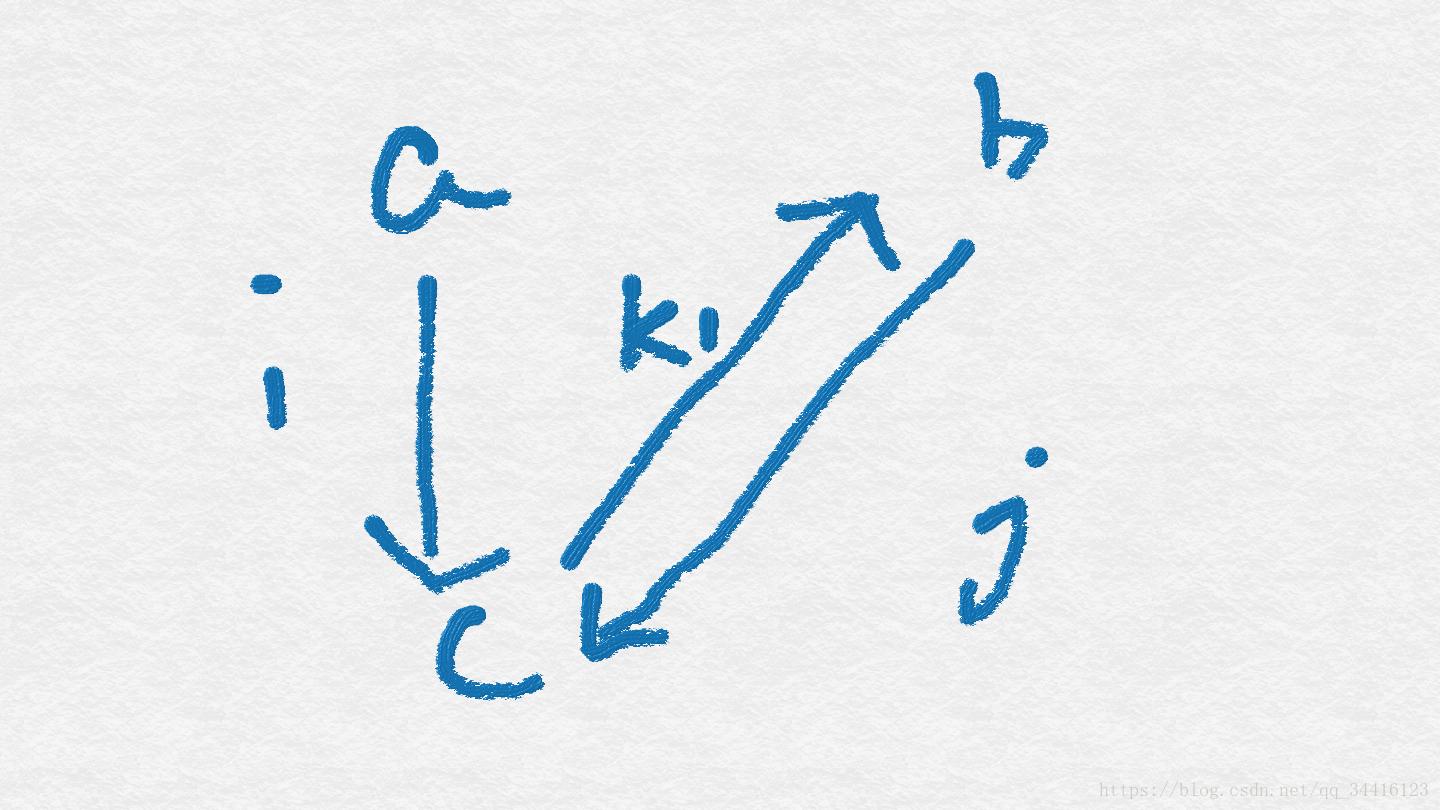
大家可以发现,在D图中, i边的起点和j边的起点无论如何都会连在同一个点上, 那么, 假设i边起点为i0, j变起点为j0,
都连在p点上。
那么在E图中如果i和j其中一个点, 比如i点, 有另外一条边连到k2的话
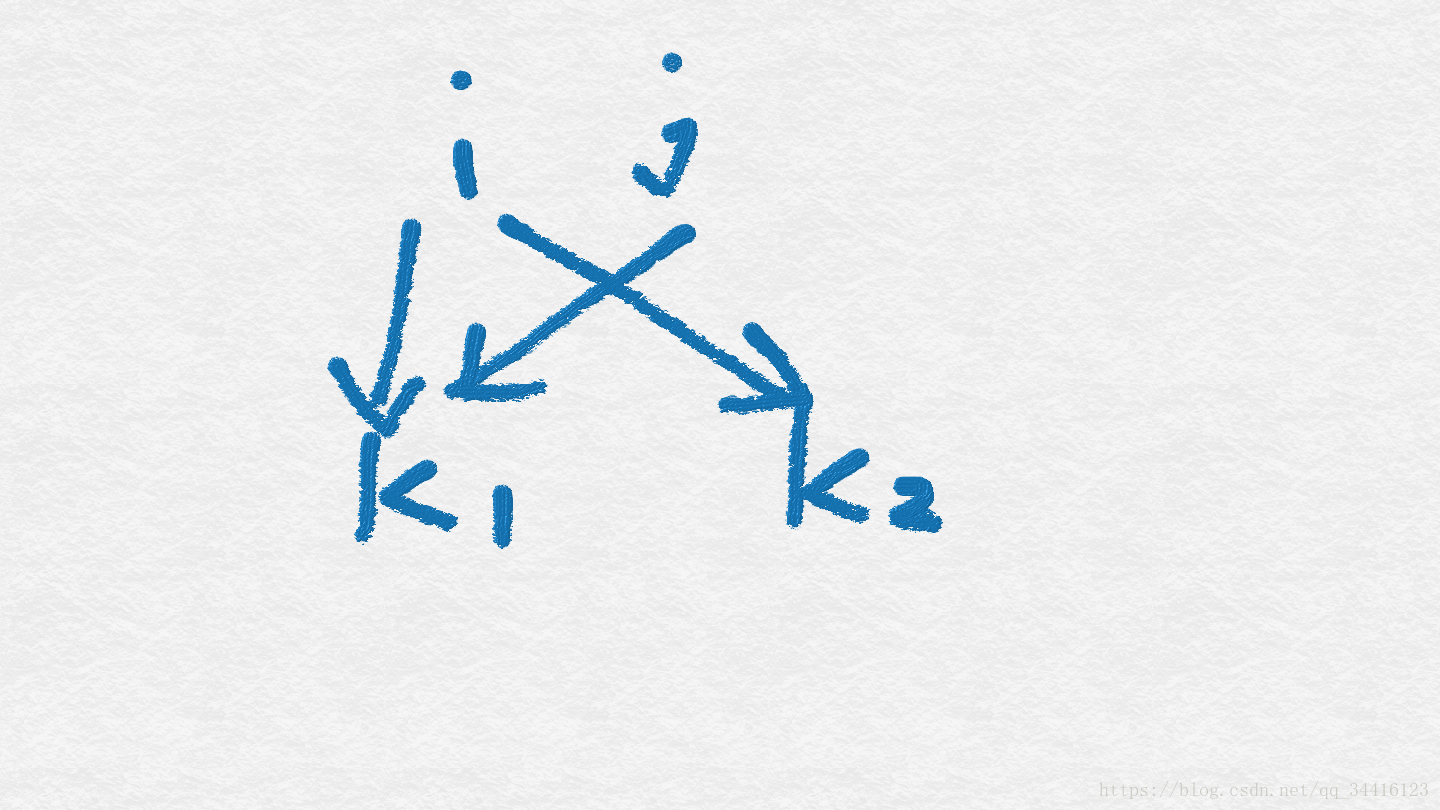
那也就是说在D图中i边的终点p多了一条连向其他点的边, 那么又因为j也连着p点, 所以在E图中必然有j到k2的一条边。
如图所示。
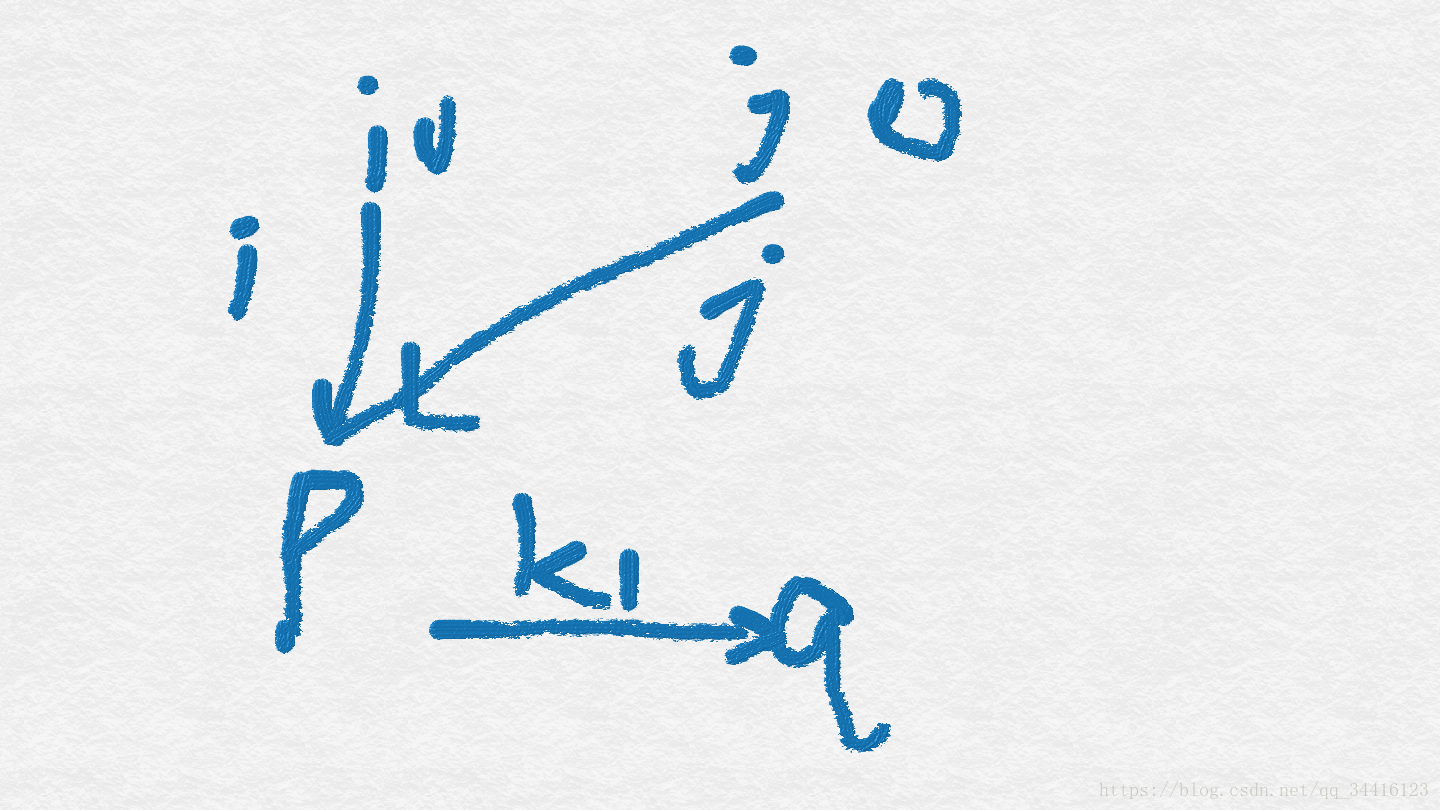
注意这个从p点出去的这个q点不一定是新的点, 也可以就是i点或者j点, 但是总之有一条边是以p点为起点的。
显然可以看到, 这个时候符合存在边jp和pq, 也就是说E图中必然还有一条边是j到k2的, 所以只要其中一个点
连到了k2, 那么另外一个点肯定存在边到k2, 不可能出现只有一个点连到k2的情况。
因此得出结论:对于E图而言,如果存在i和j结点到k1都有边,而i和j中只有一个结点到k2有边,则这个图是不可能转化来的。#include<cstdio>
#include<cstring>
#define REP(i, a, b) for(int i = (a); i < (b); i++)
using namespace std;
const int MAXN = 312;
int g[MAXN][MAXN], n, m;
bool judge()
{
REP(i, 0, n)
REP(j, 0, n)
{
bool ok1 = false, ok2 = false;
REP(k, 0, n)
{
if(g[i][k] && g[j][k]) ok1 = true;
if(g[i][k] ^ g[j][k]) ok2 = true;
}
if(ok1 && ok2) return false;
}
return true;
}
int main()
{
int T, kase = 0;
scanf("%d", &T);
while(T--)
{
memset(g, 0, sizeof(g));
scanf("%d%d", &n, &m);
REP(i, 0, m)
{
int x, y;
scanf("%d%d", &x, &y);
g[x][y] = 1;
}
printf("Case #%d: %s
", ++kase, judge() ? "Yes" : "No");
}
return 0;
}