绪论
算法:即是在特定计算模型下,旨在解决特定问题的指令序列
要保证正确性、确定性、可行性、有穷性
有穷性:
例子1:HailStone序列

@Test
public void test1() {
int n = 7;
int length = 1;
while (n > 1) {
n = ((n % 2) > 0) ? 3 * n + 1 : n / 2;
length++;
}
System.out.println(length);
}
层级级别:

例子2:计算任意N个整数之和
减而治之
@Test
public void test4() {
int[] A = {100, 836, 3236, 5, 16, 26, -3, 89, 69, 43};
long begintime = System.nanoTime();
/*int n = A.length;//简单递归
System.out.println(sum1(A,n));*/
int lo = 0;//二分递归
int hi = A.length - 1;
System.out.println(sum2(A, lo, hi));
long endtime = System.nanoTime();
long costTime = (endtime - begintime);
System.out.println(costTime);
}
public int sum1(int A[], int n) {
return (n < 1) ? 0 : sum1(A, n - 1) + A[n - 1];
}
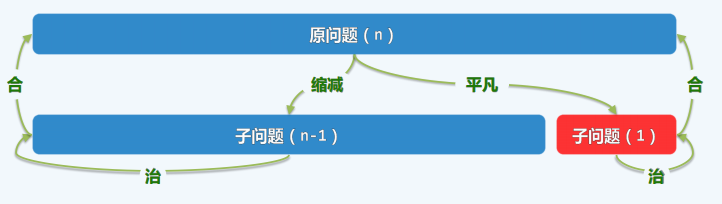
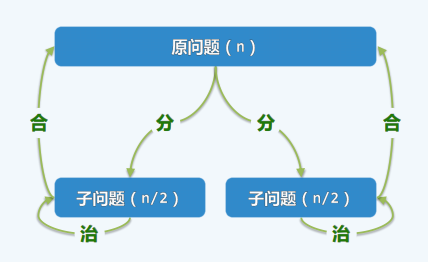
分而治之
public int sum2(int A[], int lo, int hi) {
if (lo == hi) {
return A[lo];
}
int mi = (lo + hi) >> 1;
return sum2(A, lo, mi) + sum2(A, mi + 1, hi);
}
数组反向
@Test
public void test5() {
int[] A = {100, 836, 3236, 5, 16, 26, -3, 89, 69, 43};
int lo = 0;
int hi = A.length - 1;
reverse(A, lo, hi);
}
public void reverse(int[] A, int lo, int hi) {
if (lo < hi) {
int a = A[lo];
A[lo] = A[hi];
A[hi] = a;
System.out.println(Arrays.toString(A));
reverse(A, lo + 1, hi - 1);
}
}
例子3:从数组区间中找出最大的两个整数元素
@Test
public void test6() {
int[] A = {100, 836, 3236, 5, 16, 26, -3, 89, 69, 43};
int lo = 0;
int hi = A.length - 1;
/*int[] int1 = max2(A, lo, hi);*/
/*int[] int2 = max02(A, lo, hi);*/
int[] int3 = max002(A, lo, hi);
System.out.println(Arrays.toString(int3));
}
public int[] max2(int[] A, int lo, int hi) {
int x1 = lo;
int x2 = lo;
//扫描lo-hi,找到x1
for (int i = lo + 1; i < hi; i++) {
if (A[x1] < A[i]) {
x1 = i;
}
}
//扫描lo-x1,找到较大值
for (int i = lo + 1; i < x1; i++) {
if (A[x2] < A[i]) {
x2 = i;
}
}
//扫描x1-hi,找到x2
for (int i = x1 + 1; i < hi; i++) {
if (A[x2] < A[i]) {
x2 = i;
}
}
return new int[]{x1, x2};
}
改进1:
public int[] max02(int[] A, int lo, int hi) {
int x1 = lo;
int x2 = lo + 1;
if (A[x1] < A[x2]){
int a = A[x1];
A[x1] = A[x2];
A[x2] = a;
}
for (int i = lo + 2;i < hi;i++){
if (A[x2] < A[i]){
if (A[x1] < A[x2 = i]){
int a = A[x1];
A[x1] = A[x2];
A[x2] = a;
}
}
}
return new int[]{x1, x2};
}
改进2:
public int[] max002(int[] A, int lo, int hi) {
int x1 = 0;
int x2 = 0;
if (lo + 1 == hi){
if (A[x1 = lo] < A[x2 = hi]){
int a = x1;
x1 = x2;
x2 = a;
}
return new int[]{x1,x2};
}
if (lo + 2 == hi){
int mid = (lo + hi)/2;
if ((A[lo] > A[mid]) && (A[lo] > A[hi])){
x1 = lo;
x2 = (A[mid] > A[hi]) ? mid:hi;
}else if((A[lo] < A[mid]) && (A[mid] > A[hi])){
x1 = mid;
x2 = (A[lo] > A[hi]) ? lo:hi;
}else{
x1 = hi;
x2 = (A[lo] > A[mid]) ? lo:mid;
}
return new int[]{x1,x2};
}
int mi = (lo + hi) / 2;
int[] L= max002(A, lo, mi);
int[] R = max002(A, mi+1, hi);
if (A[L[0]] > A[R[0]]){
x1 = L[0];
x2 = (A[L[1]] > A[R[0]]) ? L[1]:R[0];
}else{
x1 = R[0];
x2 = (A[L[0]] > A[R[1]]) ? L[0]:R[1];
}
return new int[]{x1,x2};
}
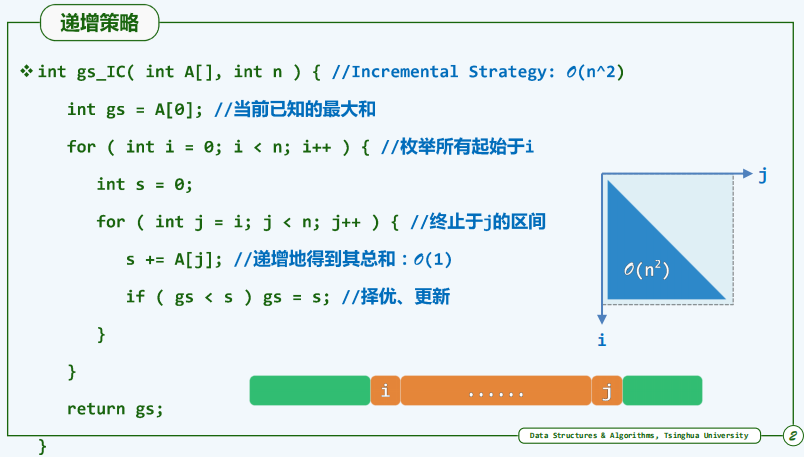
例子3.5:最大综合区间(还没写)
蛮力

递增
分治

减治

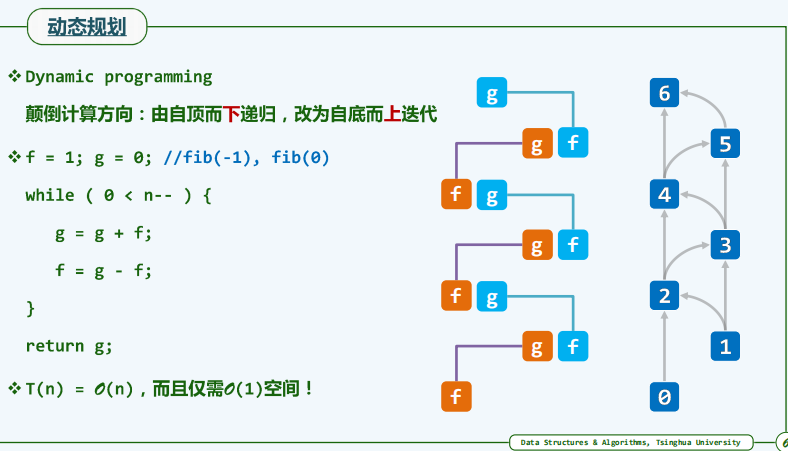
例子4:斐波那契数列
@Test
public void test7(){
for (int i = 0;i < 25;i++){
System.out.println(fib(i));
}
}
public int fib(int n){
int f = 0;
int g = 1;
while(0 < n--){
g = g + f;
f = g - f;
}
return g;
}
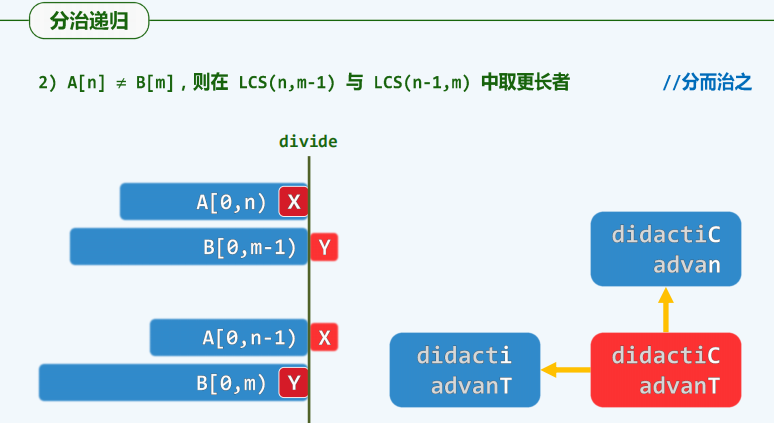
例子5:最长公共子序列
情况分析

@Test
public void test8(){
char[] x = {'A','B','C','B','D','A','B'};
char[] y = {'B','D','C','A','B','A'};
int[][] b = new int[x.length+1][y.length+1];
int[][] c = lcsLength(x,y,b);
System.out.println(c[x.length][y.length]);
lcs(x.length,y.length,x,b);
}
//从[0][0]向[x.length+1][y.length+1]不断的得到1、共同序列个数 2、各种情况并作出标记
public int[][] lcsLength(char[] x,char[] y,int[][] b) {
//给第一行,第一列设置空序列
int[][] c = new int[x.length+1][y.length+1]; //0存空序列
for(int i=0;i<c.length;i++){
for(int j=0;j<c[0].length;j++){
c[i][j] = 0;
}
}
//进行规划
for (int i = 1;i <= x.length;i++){
for (int j = 1;j <= y.length;j++){
//情况一、末位相等,去除最后一个值并比较前面的(减而治之)
if (x[i-1] == y[j-1]){
c[i][j] = c[i-1][j-1]+1;
b[i][j] = 1;
}else{
//情况二、不相等,分别去除其中一个数列的末位并进行比较(分而治之)
if(c[i-1][j]>=c[i][j-1]){
c[i][j] = c[i-1][j];
b[i][j] = 2;
}else{
c[i][j] = c[i][j-1];
b[i][j] = 3;
}
}
}
}
//返回规划好的情况c
return c;
}
public void lcs(int i,int j,char[]x,int[][]b){
//结束条件
if (i==0 || j==0){
return;
}
//判断b[i][j]进入不同分支
if (b[i][j]==1){
//减而治之
lcs(i-1,j-1,x,b);
System.out.print(x[i-1]);
}else {
//分而治之
if (b[i][j] == 2){
lcs(i-1,j,x,b);
}else{
lcs(i,j-1,x,b);
}
}
}
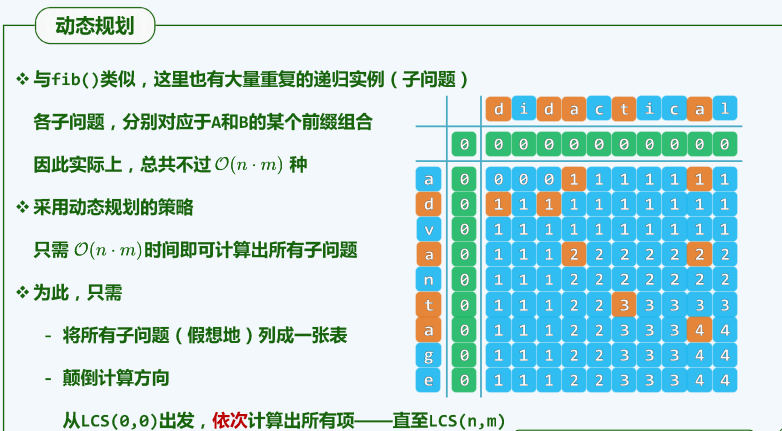
空间优化
/**
* 方法二、进行空间上的优化
* 通过状态方程可知,计算c[i][j]时只需知道c[i-1][j-1]、c[i-1][j]、c[i][j-1]就行了
* 那么就和斐波那契数列比较相似,可以利用滚动数组
*/
//从[0][0]向[x.length+1][y.length+1]不断的得到1、共同序列个数 2、各种情况并作出标记
public Set<Character> lcsLength2(char[] x, char[] y) {
Set<Character> set = new HashSet<>();
//给第一行,第一列设置空序列
int[][] c = new int[x.length+1][y.length+1]; //0存空序列
for(int i=0;i<c.length;i++){
for(int j=0;j<c[0].length;j++){
c[i][j] = 0;
}
}
//进行规划
for (int i = 1;i <= x.length;i++){
for (int j = 1;j <= y.length;j++){
//情况一、末位相等,去除最后一个值并比较前面的(减而治之)
if (x[i-1] == y[j-1]){
c[i%2][j] = c[(i-1)%2][j-1]+1;
char a = y[j-1];
set.add(a);
}else{
//情况二、不相等,分别去除其中一个数列的末位并进行比较(分而治之)
c[i%2][j] = Math.max(c[i%2][j-1],c[(i-1)%2][j]);
}
}
}
//返回规划好的情况c
return set;
}
递归版本(没写JAVA版的)
function LCS(str1, str2, a, b) {
if(a === void 0){
a = str1.length - 1
}
if(b === void 0){
b = str2.length - 1
}
if(a == -1 || b == -1){
return 0
}
if(str1[a] == str2[b]) {
return LCS(str1, str2, a-1, b-1)+1;
}
if(str1[a] != str2[b]) {
var x = LCS(str1, str2, a, b-1)
var y = LCS(str1, str2, a-1, b)
return x >= y ? x : y
}
}