1. vi和vim介绍
vim是vi的升级版。都是Linux系统环境下的文件编辑器
2. 进入vim编辑器
vim 文件名(注:若文件名存在,则打开这个文件;文件名如果不存在,仍然能够进入vim编辑器,保存后退出会创建这个名字的文件
3. 退出
在退出之前,若在编辑状态按键盘上的【Esc】键
1) 不保存退出 :q
2)保存退出 :wq
3) 不保存强制退出 :q!
4. 输入内容
vim有三种模式:分别是命令模式;编辑模式;底行模式。三种可以相互切换
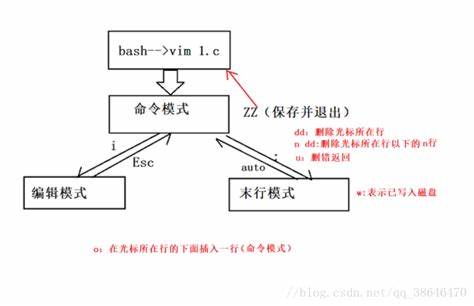
(图片来自网络)
1) 按【i】/【o】/【a】键进入编辑模式 可自由输入
【i】表示以插入方式编辑,类似于平时的insert编辑方式;
【o】表示以open方式编辑,即该方式下 会另起一行进行编辑;
【O】表示以Open方式编辑,即该方式下 在上一行进行编辑;
【a】表示以追加方式(append)编辑,在当前光标的下一个字母开始编辑;
【A】表示以追加方式(Append)编辑,在当前光标行的末尾开始编辑;
2) 按【Esc】键退出编辑模式进入命令模式,此时可照第3条的方式退出
5. 在命令模式下,浏览文件内容常用操作
1) 使用【:set nu】显示行号
2) 输入大写字母【G】,把光标定位到最后一行
3) 输入【gg】,回到第一行
4) 上下左右移动光标
① ↑ ↓ ← →
② H J K L
6. 在命令模式下,编辑内容的常用命令
1) 【dd】表示删除当前行
2) 【u】 撤销刚才的操作
3) 【Ctrl + r】 重做刚才的操作
4) 【yy】 复制当前行
5) 【p】 将剪切板的内容粘贴到当前行的下一行
7. 在命令模式下的搜索
格式: /关键词
搜索的结果使用【n】表示往下一个,【N】表示往上一个
8. 在命令模式下的区块操作
使用【Ctrl + V】 进入区块操作,然后按上下左右键可选定执行区块操作的范围,对选中的进行操作。可使用【Shift + I】 进入编辑模式进行编辑
9. 在命令模式下替换用法
1)将光标所在位置的 abc 替换为 xyz,那么就这样:【:s/abc/xyz/】,即格式为:【:s/】
2)将光标所在行的abc替换为xyz,那么就这样:【:s/abc/xyz/g】,即格式为:【:s/xx/xxx/g】
3)替换文件中所有行中的 abc替换为xyz,只需在替换命令的最前面加上了“1,$”,类似与“m,n”的格式,那么就这样:【:1,$s/abc/xyz/g】,格式为:【:1,$s/xx/xxx/g】
转义替换:
4)当前行里所有的“S.”替换为“S->”,就需要用到转义符:【:s/S./S->/g】。因为点号“.”为特殊匹配符,在正则中表示单个字符,所以如果想匹配点号,就需要把“”放在点号前面,表示取消点号的特殊意义。
5)将aaa 2008-07-01 bbb 替换为 aaa '2008-07-01' bbb, 则这样写:【:1,$s/([0-9]{4}-[0-9]{2}-[0-9]{2})/'1'/g】
还有其他更复杂的,我们要逐步解释一下,这里面共涉及了三个知识点:
第一个知识点:[0-9] 表示 0 到 9 之间的任一个数字,这是正则中表示数字集合的标准写法。
第二个知识点:{n} 表示将此符号前面的元素重复 n 遍,所以 [0-9]{4} 就表示一个四位数的数字。
第三个知识点:如果在匹配方案中用到了(),则表示要暂存括号中所匹配到的内容,而 1 表示替换为暂存的内容(题外话:如果存在多个括号组,则后面要通过编号来依次对应,如 1、2、3 等)。