提起排序,与我们的息息相关,平时开发的代码少不了排序。
经典的排序算法又非常多,我们怎么评价一个排序算法的好坏呢?
其实可以这样想,要细致的比较排序算法好坏,那我们就从多方面尽可能详细的对比
一、效率方面
1、排序算法的执行效率:最好、最坏、平均
2、 我们之前舍弃的时间复杂度的系数、常量、低阶,在这里需要拿回来
3、排序,免不了比较和移动
二、内存消耗方面
没错就是 算法的空间复杂度,不过对于排序的空间复杂度来说,又赋予了新的名词 — 原地排序。
顾名思义是 原地排序的肯定是消耗内存少,反之需要往外走几步那就需要临时申请内存了。
原地排序 = O(1)
三、算法稳定性
字面意义就是不论怎么摆弄,这个算法稳定,不会对顺序有影响。
上面这句话应该加上一个定语:对于拥有相同值的元素的前后顺序不会发生改变。
举个例子:有两个对象,其中的金额字段一样,按照金额排序,经过算法一顿折腾后,相同金额的对象先后顺序不能发生改变。
讲完评估排序算法的优劣的几个方面,那就直接看看我们平时常见的几个经典算法:
1、冒泡排序
图例演示
> C#
1 //排序 — 冒泡排序 2 private static void BubbleSort(int[] source) 3 { 4 if (source.Length <= 1) 5 return; 6 7 bool isChanged = false; 8 for (int i = 0; i < source.Length; i++) 9 { 10 for (int j = 0; j < source.Length - i - 1; j++) 11 { 12 var left = source[j]; 13 var right = source[j + 1]; 14 Console.WriteLine("【比较】"); 15 if (left <= right) 16 continue; 17 18 source[j] = right; 19 source[j + 1] = left; 20 isChanged = true; 21 Console.WriteLine("{交换}"); 22 } 23 if (!isChanged) 24 break; 25 } 26 Printf(source); 27 }
Q:冒泡排序的时间算法复杂度
A:最坏时间复杂度 — O(n^2):循环 n*n次
最好时间复杂度 — O(n) :循环 n次即可
平均时间复杂度 — O(?)
这里我们使用概率来分析平均复杂度,情况比较复杂。
我们使用一种新的概念来分析平均复杂度,这个就是 有序度。
有序度:看作是向量,左<= 右
逆序度:正好相反,左 >= 右
满有序度 = n*(n-1) / 2
逆序度 = 满有序度 - 有序度
对于 n 个数据来说,最坏情况时间复杂度的有序度是0,要交换 n*(n-1)/2次才能正确输出。
对于最好情况复杂度的有序度是n*(n-1)/2,需要交换0次就能达到完全有序。
最坏 n*(n-1)/2次,最好0次,取个中间值来表示中间情况,也可以看作是平均情况 n*(n-1) /4
所以平均下来 要做 n*(n-1) / 4 次才能有序,因为冒泡排序的时间复杂度的上限是 O(n^2)
所以平均情况时间复杂度为 O(n^2)
虽然这样推论平均个情况并不严格,但是比起概率推论来说,这样简单且有效。
Q:冒泡排序是不是原地排序
A:是,临时变量为了交换数据,常量级别的临时空间申请,所以空间复杂度为O(1)
Q:冒泡排序是不是稳定排序
A:是,因为没有改变相同元素的先后顺序。
2、插入排序
假定,我们将排序串分为两个区:已排序区,未排序区
一个元素要找到正确的的位置进行插入,那么需要去已排序区域找到自己的位置后,
将这个位置的元素们向后移动,空出位置,然后新元素入坑。
从以上这个思路来看,插入排序也是涉及到了元素的比较和移动。
给我们一个无序数组,哪块是已排序区?哪里是未排序区?
比如:9, 0, 1, 5, 2, 3, 6
初始时,9 就是已排序区域;
0开始去已排序区域挨个比较,即 i=1,0<9,9向后挪动,空出位置,0入坑;
1开始去 [ 0,9 ] 已排序区域比较,1 < 9,9向后移动腾位置,1入坑,1 > 0 无需操作;
依次重复以上操作,即可达成有序。
图例演示
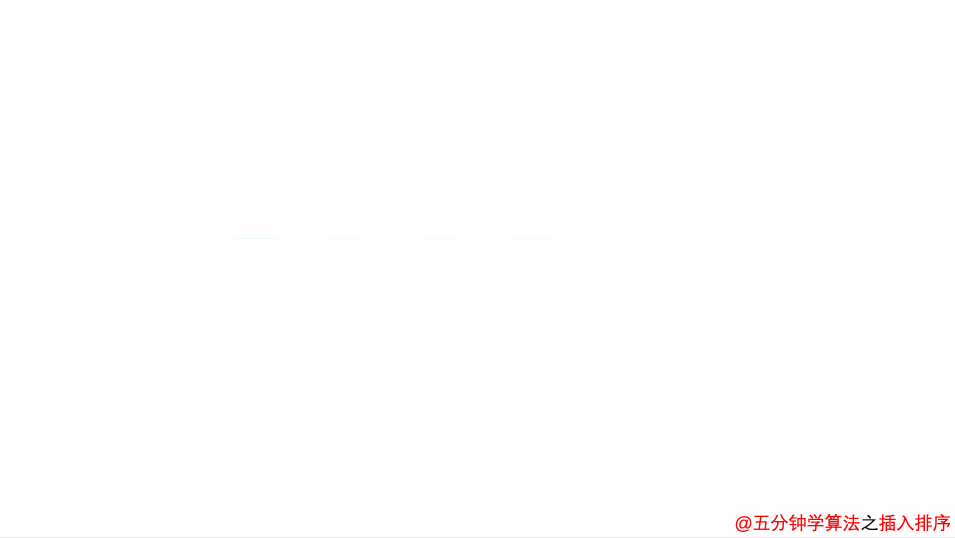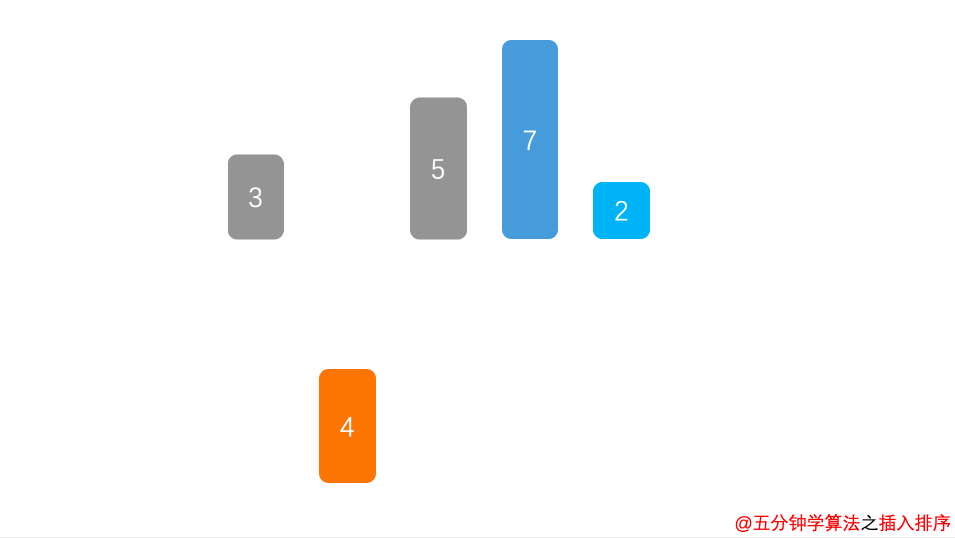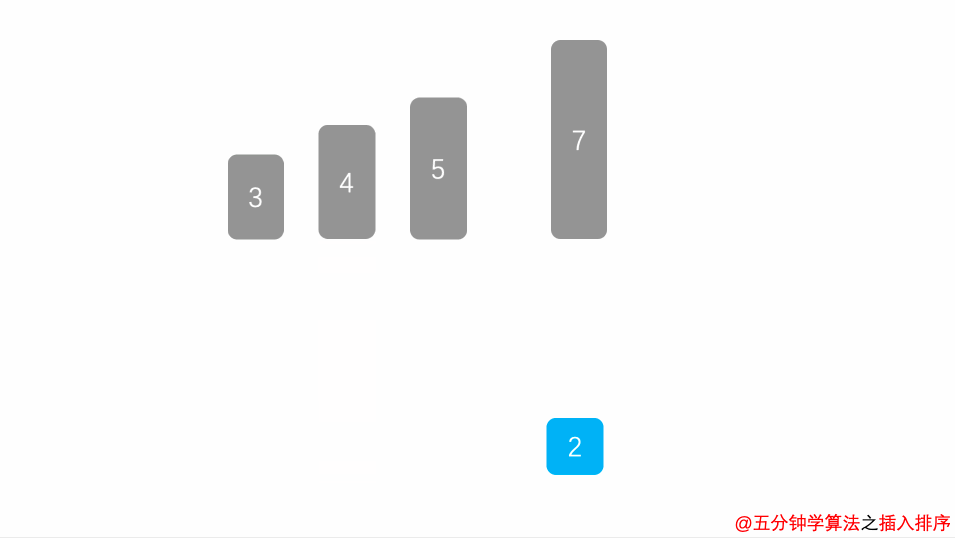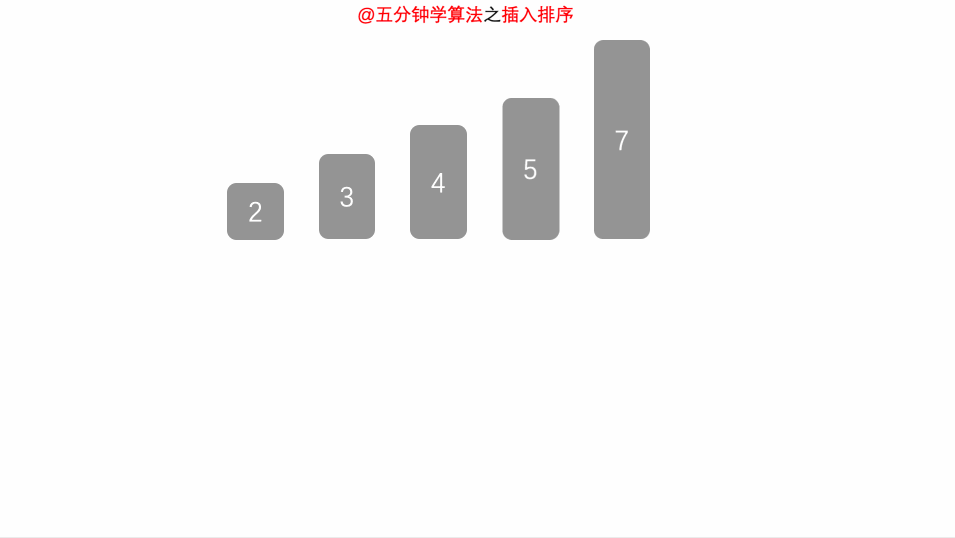
> C#
1 //排序 — 插入排序 2 private static void InsertionSort(int[] source) 3 { 4 if (source == null || source.Length <= 0) 5 return; 6 7 for (int i = 1; i < source.Length; i++) 8 {// 未排序区 9 var sorting = source[i]; 10 int j = i - 1; 11 12 for (; j >= 0; j--) 13 {// 已排序区 14 15 // 比较 16 if (sorting >= source[j]) 17 { 18 break; 19 } 20 21 // 后移 22 source[j + 1] = source[j]; 23 } 24 25 // 入坑 26 source[j + 1] = sorting; 27 } 28 Printf(source); 29 }
Q:插入排序的时间算法复杂度
A:最坏时间复杂度 — O(n^2):完全倒序,循环n次,比较n次
最好时间复杂度 — O(n):完全有序,循环n次跳出
平均时间复杂度 — O(n^2):循环 n次数据,在一个数组中插入数据的平均情况时间复杂度为O(n),所以是 O(n^2)
Q:插入排序是不是原地排序
A:是,没有临时变量申请,所以空间复杂度为O(1)
Q:插入排序是不是稳定排序
A:是, if (sorting >= source[j]) 这个判断保证了相同元素的先后顺序不变,
去掉等于号也可以发生改变。可以实现稳定排序所以说是稳定排序
开始我们也说了,这么多排序算法,我们要对比一下,择优选择。
| 排序 | 最好情况 | 最坏情况 | 平均情况 | 是否稳定 | 是否原地 |
| 冒泡 | O(n) | O(n^2) | O(n^2) | 是 | 是 |
| 插入 | O(n) | O(n^2) | O(n^2) | 是 | 是 |
那么问题来了平均都是 O(n^2),为什么倾向于使用插入排序呢?
这两种排序我们将常量都放进来会发现,冒泡使用的常量数比排序多,所以在数据量上来后 常量*n 会有很大的差距。
我们的编程语言中的排序算法很多都会倾向于插入排序算法。
3、选择排序
其实操作类似于插入排序,只不过是换了换操作方式。
所以也分为 已排序区和未排序区,操作方式是在未排序区间找到最小的,然后放到已排序区间最后。
图例:
> C#
private static void SelectionSort(int[] source) { if (source.Length <= 1) return; for (int i = 0; i < source.Length - 1; i++) {// 已排序 var minIndex = i; for (int j = i+1; j < source.Length; j++) {//未排序 if (source[minIndex] > source[j]) { minIndex = j; } } if (i != minIndex) { int tmp = source[i]; source[i] = source[minIndex]; source[minIndex] = tmp; } } Printf(source); }
Q:选择排序的时间算法复杂度
A:最坏时间复杂度 — O(n^2)
最好时间复杂度 — O(n^2)
平均时间复杂度 — O(n^2)
Q:选择排序是不是原地排序
A:是,没有临时变量申请,所以空间复杂度为O(1)
Q:选择排序是不是稳定排序
A:不是
4、对比 随机生成1000个元素的 int 数组
分别执行时间如下:


