归并排序比较适合大规模得数据排序,借鉴了分治思想。
归并排序原理

自古以来,分久必合合久必分。
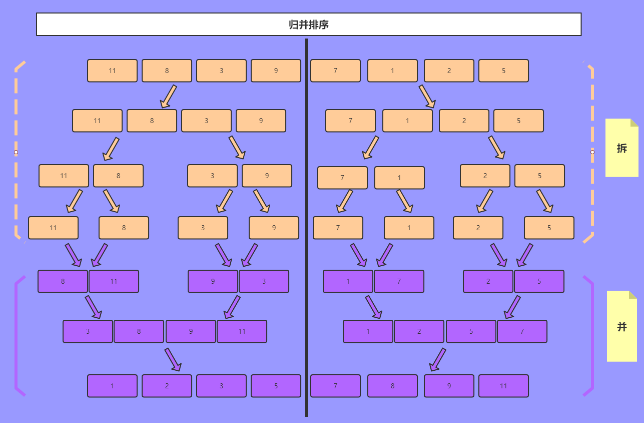
我们可以这样理解归并排序,分-分到不能分为止,然后合并。
使用递归将问题一点一点分解,最后进行合并。
分而治之 (merge_sort)
提到递推,我们使用地递推解决问题,首先要分析出递推公式、明确结束条件。
递推公式: merge_sort(i...n)=merge( merge_sort(i...j), merge_sort(j+1...n) ) 结束条件: i>=n
分久必合(merge)
将两个有序的数组进行合并,这样整个数组也就是排序好的数组了。
那么怎么进行合并呢?-- (i...j) 和 (j+1...n) 重新排序后,重新放入原来的数组 (i...n)
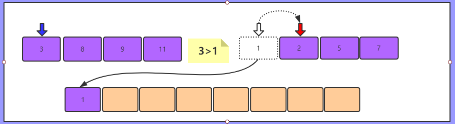
两组数组 [3, 8, 9, 11] vs [1, 2, 5, 7]
两个游标 蓝色 和 红色
3>1,1小,1入新数组,红色游标后移一位,继续比较...
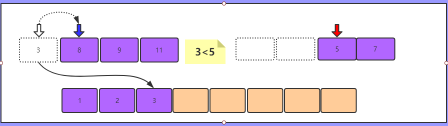
3>2,2小,2入数组,红色游标后移一位

3<5,3小,3入数组,蓝色游标后移一位
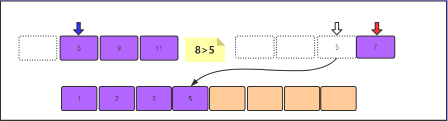
8>5,5小,5入数组,红色游标后移一位
8>7,7小,7入数组,红色游标后移,右侧数组全部转移完毕
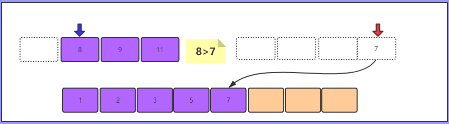
当有一组数组全部转移完毕,那么剩下的一组中的全部元素依次转入到新数组中,新数组正式成为一个有顺序的数组

通过以上两点:递推公式和合并思想,我们使用代码实现一下:
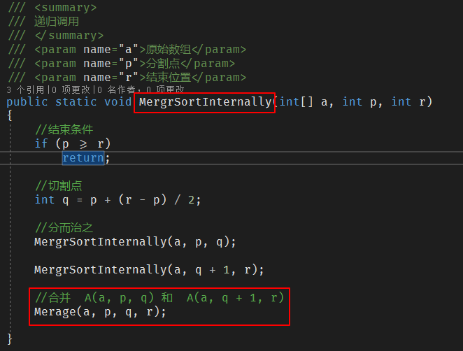
1、如下图:递归方式 进行分解,然后使用合并代码进行合并。

1 /// <summary> 2 /// 递归调用 3 /// </summary> 4 /// <param name="a">原始数组</param> 5 /// <param name="p">分割点</param> 6 /// <param name="r">结束位置</param> 7 public static void MergrSortInternally(int[] a, int p, int r) 8 { 9 //结束条件 10 if (p >= r) 11 return; 12 13 //切割点 14 int q = p + (r - p) / 2; 15 16 //分而治之 17 MergrSortInternally(a, p, q); 18 19 MergrSortInternally(a, q + 1, r); 20 21 //合并 A(a, p, q) 和 A(a, q + 1, r) 22 Merage(a, p, q, r); 23 24 }
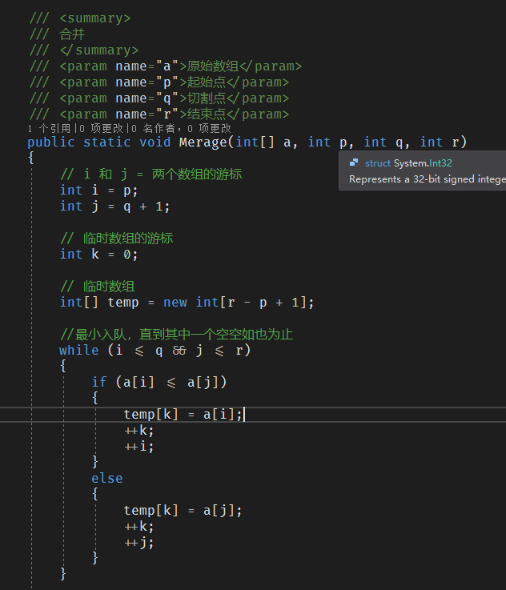
2、我们再来看看合并逻辑
参数:原始数组,开始的地方,切割的地方,结束的地方
逻辑:两个切割数组的各自的游标
申请同样大小的临时数组
循环比较;小的入临时,游标后移;知道有一个数组空了为止
找到剩下不为空的那个数组,将剩余元素入临时
将临时数组,找到原始数组的对应为止进行覆盖

1 /// <summary> 2 /// 合并 3 /// </summary> 4 /// <param name="a">原始数组</param> 5 /// <param name="p">起始点</param> 6 /// <param name="q">切割点</param> 7 /// <param name="r">结束点</param> 8 public static void Merage(int[] a, int p, int q, int r) 9 { 10 // i 和 j = 两个数组的游标 11 int i = p; 12 int j = q + 1; 13 14 // 临时数组的游标 15 int k = 0; 16 17 // 临时数组 18 int[] temp = new int[r - p + 1]; 19 20 //最小入队,直到其中一个空空如也为止 21 while (i <= q && j <= r) 22 { 23 if (a[i] <= a[j]) 24 { 25 temp[k] = a[i]; 26 ++k; 27 ++i; 28 } 29 else 30 { 31 temp[k] = a[j]; 32 ++k; 33 ++j; 34 } 35 } 36 37 // 找到另一个不为空的,找到剩下的元素 38 int start = i; 39 int end = q; 40 41 if (j <= r) 42 { 43 start = j; 44 end = r; 45 } 46 47 // 剩余数组拷贝到临时数组 temp 48 while (start <= end) 49 { 50 temp[k++] = a[start++]; 51 } 52 53 // 将temp覆盖到a[p...r] 54 for (i = 0; i <= r - p; ++i) 55 { 56 a[p + i] = temp[i]; 57 } 58 }

归并排序性能分析
Q:是不是稳定排序?
A:是
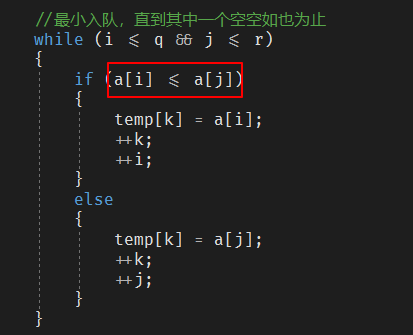
对于这两组数组 A[p...q] 和 A[q+1...r] 来说
代码中也是这样实现的,a[i]就是左侧数组,a[j]就是右侧数组,保证相等时左侧优先入队即可。注意 等号位置。
Q:是否是原地排序?
A:当然不是
因为我们在合并代码时候,申请了同样大小的内存空间。
但是对于这里的归并排序的空间复杂度又是多少呢?
虽然牵扯到了递归,但是临时变量这里会在一个函数结束后栈会释放,所以空间复杂度是O(n)
Q:时间复杂度又是多少呢?
A:O(n log n)
我们对 n 个元素的归并排序时间记作 T(n),
分解函数分解两个子数组的时间是T(n/2)
合并函数时间复杂度是O(n)
T(1)=C; n=1
T(n)=2*T(n/2)+ n; n>1
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2^k * T(n/2^k) + k * n
T(n) = 2^k * T(n/2^k) + k * n
当 T(n/2^k) = T(1)=> k = log2 n
即:T(n) = Cn + n log2 n => O(n log n)
