2.4 选择第k大的元素 selection

1.目标：找到N个元素中，第k大的数。

   例如：max是k=N--1；min是k=0；median是k=N/2

2.Quick-select 借鉴了快速排序的思想

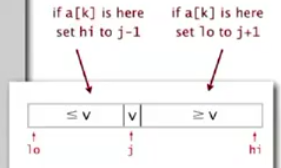
（1）利用partition保证：

　　①a[j] is in place

　　②左边的元素不大于a[j]，右边的元素不小于a[j]

（2）在其中一个子数组中重复划分，当j=k时结束

3.实现

package com.cx.sort;

public class QuickSelect {
    public static Comparable select(Comparable[] a,int k) {
        //打乱数组,避免出现最坏情况，平方时间
        Shuffling.sort(a);
        int lo=0,hi=a.length-1;
        while(hi>lo) {
            //j in place
            int j=partition(a, lo, hi);
            //如果j<k,只需要重新划分右边的数组
            if(j<k) lo=j+1;
            //如果j>k,只需要重新划分左边的数组
            else if(j>k) hi=j-1;
            else  return a[k];            
        }
        return a[k];
    }

    //划分,使得j左边的数不大于a[j],j右边的数不小于a[j]
    private static int partition(Comparable[] a,int lo,int hi) {
        int i=lo,j=hi+1;
        //1.repeat
        while(true) {
            //1)循环i,直到大于a[lo]
            while(less(a[++i], a[lo])) 
                //不可少，防止出现dcba时，i越界
                if(i==hi) break;
            //2)循环j,直到小于a[lo]
            while(less(a[lo], a[--j]))
                if(j==lo) break;
            //3)判断是否交叉
            if(i>=j) break;
            exch(a, i, j);            
        }
        //2.交叉后，交换lo,j
        exch(a, lo , j);
        //j in place
        return j;
    }
    
    private static boolean less(Comparable v,Comparable w) {
        return v.compareTo(w)<0;
    }
    
    private static void exch(Comparable[] a,int i ,int j ) {
        Comparable t=a[i];
        a[i]=a[j];
        a[j]=t;
    }
    private static void show(Comparable[] a) {
        for(int i=0;i<a.length;i++) {
            System.out.print(a[i]+" ");
            
        }
        System.out.println();
    }
    public static void main(String[] args) {
        String a[]= {"s","o","r","t","e","x","a","m","p","l","e"};
        show(a);
        //第几大的数(k=0..N-1)
        int k=3;
         System.out.println("第"+k+"大的数是:"+select(a, k));

    }
}

package com.cx.sort;

public class Shuffling {
    public static void sort(Comparable[] a) {
        int N=a.length;
        for(int i=1;i<N;i++) {
            //第i次迭代，随机找r，r是0-r的随机数
            int r=(int)(Math.random()*(i+1));
            exch(a, i, r);
        }
    }
    
    private static boolean less(Comparable v,Comparable w) {
        return v.compareTo(w)<0;
    }
    
    private static void exch(Comparable[] a,int i ,int j ) {
        Comparable t=a[i];
        a[i]=a[j];
        a[j]=t;
    }
    private static void show(Comparable[] a) {
        for(int i=0;i<a.length;i++) {
            System.out.print(a[i]+" ");
            
        }
        System.out.println();
    }
    public static void main(String[] args) {
        String a[]= {"s","o","r","t","e","x","a","m","p","l","e"};
        show(a);
        sort(a);
        show(a);
    }
}

4.说明：

（1）quick-select:平均花费线性时间，最差的情况是~1/2N²

         最差的情况发生在正序或倒序的时候，但是第一步的shuffling可以有效的避免这种情况。

　　 线性时间可以简单的N+1/2N+1/4N+..=~2N

（2）常系数还是相对大了，还需要继续改进算法。