在学习完普利斯顿算法该部分和Algorithms第四版第二章以后,对几大经典排序算法的思想和java实现进行总结,包括选择排序,插入排序,希尔排序,归并排序,快速排序以及堆排序。
一.选择排序 selection sort
1.基本思想:i遍历数组,一直在未分类的元素中找最小的元素,并与a[i]交换
2.代码实现

package com.cx.sort; public class Selection { public static void sort(Comparable[] a) { for(int i=0;i<a.length-1;i++) { int min=i; for(int j=i+1;j<a.length;j++) { if(less(a[j], a[min])) min=j; } exch(a, i, min); } } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; show(a); sort(a); show(a); } }
3.几点说明:
(1)大约需要N2/2次比较和N次交换
(2)在初始逆序的时候,性能很差
二.插入排序 insection sort
1.基本思想:类似整理牌的过程。第i次迭代,将a[i]依次与前面的元素进行比较,并将a[i]插入到合适的位置
2.代码实现:

package com.cx.sort; public class Insertion { public static void sort(Comparable[] a) { for(int i=1;i<a.length;i++) { //第i次迭代 for(int j=i;j>0 && less(a[j], a[j-1]);j--) { exch(a, j, j-1); } } } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; show(a); sort(a); show(a); } }
3.几点说明:
(1)对部分有序的数组很快,线性时间。
部分有序指数组中倒置的数量小于数组大小的某个倍数,例如如下场景:
①数组中每个元素距离它的最终位置不远
②一个有序的大数组接一个小数组
③数组中只有几个元素的位置不正确
(2)对于小数组很快,因此有时候对归并排序和快速排序进行优化时,分解为小数组以后,使用插入排序完成后续的工作。
(3)具有稳定性。使用不同标准进行排序,能保证key相等的元素依旧有序。
比如:歌曲先按时间排序,再按歌手排序,稳定性可以保证歌手相同的情况下,时间是有序的。
三.希尔排序Shell sort
1.出发点:考虑到插入排序对部分有序的数组和小数组进行排序时,很快,能不能使用一些方法,让数组部分有序以提高性能呢?
2.基本思想:每次使用插入排序的思想,但是不是比较并交换相邻的元素,而是使用一个距离h,每次对距离为h的小数组进行排序,不断减小h的值,直至1即完成排序。
例如:取h=1,4,13...(3x+1),先对相距13的元素组成的小数组进行排序,再对相距4的小数组进行排序,最后对相邻的数组进行排序。即可充分利用小数组和部分有序的性质,提高性能。
3.代码实现

package com.cx.sort; public class ShellSort { public static void sort(Comparable[] a) { int h=1; int N=a.length; //h的初值 while(h<N/3) h=h*3+1; while(h>=1) { //每一次进行插入排序 for(int i=1;i<N;i++) { for(int j=i;j>=h && less(a[j], a[j-h]);j-=h) { exch(a, j, j-h); } } h=h/3; } } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; show(a); sort(a); show(a); } }
4.说明:
(1)该算法的性能因为取决于h,现在也没有证明最好的递增序列是什么。但是可以确定的是最好情况下,使用线性时间
(2)希尔排序的性能优于插入排序和选择排序,小于O(N2),并且数组越大,优势越大。
(3)不要使用2的幂次作为h,因为这样的话,有些元素不到最后永远都访问不到。
四.自顶向下的归并排序 Up-Buttom merge sort
1.基本思想:要将一个数组排序,可以先递归的将它分为两半分别排序,然后将结果归并起来
2.原地归并的抽象方法
①基本思想:把涉及到的所有元素复制到一个辅助数组,再把归并的结果放回原数组。
②过程: 比较两个子数组的元素的大小,将小的赋值给原数组。
③归并的前提:两个子数组均是有序的。
④代码实现

//merge(前提是a[lo..mid]和a[mid+1..hi]分别是排好序的) public static void merge(Comparable[] a,Comparable[] aux,int lo,int mid,int hi) { //保证前提正确,帮助检查逻辑bug,如果false,会抛异常 //使用java -ea(-da) MyProgram测试,默认是da // assert isSorted(a,lo,mid); // assert isSorted(a, mid+1, hi); //将数组a复制到aux辅助数组 for(int k=lo;k<=hi;k++) { aux[k]=a[k]; } int i=lo,j=mid+1; //归并 for(int k=lo;k<=hi;k++) { if(i>mid) a[k]=aux[j++]; else if(j>hi) a[k]=aux[i++]; else if(less(aux[j], aux[i])) a[k]=aux[j++]; //保证是稳定的 else a[k]=aux[i++]; } // assert isSorted(a, lo, hi); }
3.基于上述原地归并的抽象方法,归并算法使用递归的方法,将大问题不断分解为小问题,然后用所有小问题的答案来解决整个大问题,即最终将有序的子数组归并为最终的排序结果。
4.归并算法完整的代码实现

package com.cx.sort; public class MergeSort { private static Comparable[] aux; public static void sort(Comparable[] a) { //只需要创建一次aux辅助数组 aux=new Comparable[a.length]; sort(a,aux,0,a.length-1); } public static void sort(Comparable[] a,Comparable[] aux,int lo,int hi) { if(hi<=lo) return; int mid=lo+(hi-lo)/2; //将子数组分别排序,再使用merge sort(a,aux,lo,mid); sort(a,aux,mid+1,hi); merge(a, aux, lo, mid, hi); } //merge(前提是a[lo..mid]和a[mid+1..hi]分别是排好序的) public static void merge(Comparable[] a,Comparable[] aux,int lo,int mid,int hi) { //保证前提正确,帮助检查逻辑bug,如果false,会抛异常 //使用java -ea(-da) MyProgram测试,默认是da // assert isSorted(a,lo,mid); // assert isSorted(a, mid+1, hi); //将数组a复制到aux辅助数组 for(int k=lo;k<=hi;k++) { aux[k]=a[k]; } int i=lo,j=mid+1; //归并 for(int k=lo;k<=hi;k++) { if(i>mid) a[k]=aux[j++]; else if(j>hi) a[k]=aux[i++]; else if(less(aux[j], aux[i])) a[k]=aux[j++]; //保证是稳定的 else a[k]=aux[i++]; } // assert isSorted(a, lo, hi); } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } //测试数组是否有序 public static boolean isSorted(Comparable[] a,int lo,int hi) { for(int i=lo;i<hi;i++) if(less(a[i], a[i-1])) return false; return true; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; show(a); sort(a); show(a); } }
5.说明:
(1)无论是怎样的数组,归并排序都可以保证有NlogN的性能。
(2)由于代码的写法,保证归并算法具有稳定性(代码中有具体注释),也就是说使用不同标准进行排序,能保证key相等的元素依旧有序。
比如:歌曲先按时间排序,再按歌手排序,稳定性可以保证歌手相同的情况下,时间是有序的。
(3)用到了一个辅助数组,需要使用额外的空间
6.一些可能的改进手段
(1)小数组采用插入排序,CUTOFF约为7。

public static void sort(Comparable[] a,Comparable[] aux,int lo,int hi) { //小数组使用插入排序 if(hi<=lo+CUTOFF-1) Insertion.sort(a,lo,hi); int mid=lo+(hi-lo)/2; sort(a,aux,lo,mid); sort(a,aux,mid+1,hi); merge(a, aux, lo, mid, hi); }
(2)如果已经有序了,即停止排序。也就是说对于两个子数组来说,如果a[mid]已经小于a[mid+1],则说明左边的数组已经全都小于右边的数组了,不需要继续归并

public static void sort(Comparable[] a,Comparable[] aux,int lo,int hi) { if(hi<=lo) return; int mid=lo+(hi-lo)/2; //将子数组分别排序,再使用merge sort(a,aux,lo,mid); sort(a,aux,mid+1,hi); //判断是否已经有序 if(!less(a[mid+1], a[mid])) return; merge(a, aux, lo, mid, hi); }
(3)消除复制到aux数组的时间,要在递归调用的每个层次交换输入数组和辅助数组的角色(难理解)

五.自底向上的归并排序 bottom-up merge sort
1.基本思想:先归并那些小数组,然后再成对归并得到的数组。首先两两归并,然后四四归并,八八归并...
2.说明:不需要使用递归
3.代码实现

package com.cx.sort; public class MergeSortBU { private static Comparable[] aux; public static void sort(Comparable[] a) { int N=a.length; aux=new Comparable[N]; //两两归并,四四归并 for(int sz=1;sz<N;sz=sz+sz) { for(int lo=0;lo<N-sz;lo +=sz+sz) { //min防止最后长度不够 merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1)); } } } //merge(前提是a[lo..mid]和a[mid+1..hi]分别是排好序的) public static void merge(Comparable[] a,Comparable[] aux,int lo,int mid,int hi) { //将数组a复制到aux辅助数组 for(int k=lo;k<=hi;k++) { aux[k]=a[k]; } int i=lo,j=mid+1; //归并 for(int k=lo;k<=hi;k++) { if(i>mid) a[k]=aux[j++]; else if(j>hi) a[k]=aux[i++]; else if(less(aux[j], aux[i])) a[k]=aux[j++]; //保证是稳定的 else a[k]=aux[i++]; } } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { // String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; String a[]= {"d","c","a","b"}; show(a); sort(a); show(a); } }
六.快速排序 quick sort
1.基本思想:
①打乱数组
②partition(划分),使得左边不大于a[j],右边不小于a[j],划分完以后a[j] in place
③递归排左边和右边的元素
2.主要过程(感觉写英文的比较好理解)
(1)repeat until i and j pointeers cross
①scan i from left to right as long as a[i]<a[lo]
②scan j from right to left as long as a[j]>a[lo]
③如果上述不满足,即a[i]大于a[lo],且a[j]<a[lo],则交换a[i]和a[j]
(2)when pointers cross,交换a[lo]和a[j],此时a[j] in place,在正确的位置

3.代码实现

package com.cx.sort; public class QuickSort { public static void sort(Comparable[] a) { //打乱数组 Shuffling.sort(a); // show(a); sort(a,0,a.length-1); } public static void sort(Comparable[] a,int lo,int hi) { if(hi<=lo) return; //j in place int j=partition(a, lo, hi); //分别递归的排左右两部分 sort(a,lo,j-1); sort(a,j+1,hi); } //划分,使得j左边的数不大于a[j],j右边的数不小于a[j] private static int partition(Comparable[] a,int lo,int hi) { int i=lo,j=hi+1; //1.repeat while(true) { //1)循环i,直到大于a[lo] while(less(a[++i], a[lo])) //不可少,防止出现dcba时,i越界 if(i==hi) break; //2)循环j,直到小于a[lo] while(less(a[lo], a[--j])) if(j==lo) break; //3)判断是否交叉 if(i>=j) break; exch(a, i, j); } //2.交叉后,交换lo,j exch(a, lo , j); //j in place return j; } private static boolean less(Comparable v,Comparable w) { return v.compareTo(w)<0; } private static void exch(Comparable[] a,int i ,int j ) { Comparable t=a[i]; a[i]=a[j]; a[j]=t; } private static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; // String a[]= {"a","b","c","d"}; // String a[]= {"d","c","b","a"}; show(a); sort(a); show(a); } }
4.说明:
(1)快速排序能保证NlogN的性能,且不会使用额外的内存空间。在实际中也是最快的
(2)需要首先把数组打乱,这是很重要的性能保证,因为在一些情况下,如本来就是有序的情况下,快速排序的性能可能很差,N2/2的时间,但是使用了shuffling,可以保证发生这种情况的概率极低
(3)不是稳定的,因为涉及远距离的元素交换。可以使用辅助数组的方法,来使它稳定,但是这样失去了快速排序算法的优势。
5.一些可能的改进手段
(1)小数组使用插入排序,CUTOFF约为10

public static void sort(Comparable[] a,int lo,int hi) { if(hi<=lo+CUTOFF-1) { Insertion.sort(a,lo,hi); return; } //j in place int j=partition(a, lo, hi); //分别递归的排左右两部分 sort(a,lo,j-1); sort(a,j+1,hi); }
(2)不是和a[lo]进行比较,而是计算子数组的一小部分元素的中位数作为切分元素,和它进行比较。

int m= medianOf3(a,lo,lo+(hi-lo)/2,hi); swap(a,lo,m);
(3)对于重复元素很多的情况,简单的快速排序算法性能不好,特别是在所有元素都相同的情况下,运行时间1/2N2
解决办法是采用一种特殊的快速排序算法,即3-way quicksort
七.堆排序 heap sort
1.充分利用堆的特点:具体见下一篇博客2.7:http://www.cnblogs.com/sunnyCx/p/8182887.html
(1)父结点不小于两个子结点
(2)最大值在根结点处
(3)当删除最大值时,可以用sink()方法,重新维持堆的性质
(4)假定堆用数组的a[1]..a[N]来表示,则对于结点k,它的父结点在k/2的地方,子结点(如果有的话)为2k和2k+1
(5)对于大小为N的堆来说,拥有子结点的索引为1..N/2
2.基本思想:
(1)构造堆。使用自上而下的方法,创建一个堆
①从拥有子结点的最底层元素开始,使用sink()方法,维持一个小堆
②不断减小k的值(自下而上,自右而左),当k=1时,保证了所有元素组成了组成了一个堆
(2)堆排序。删除堆的根结点,然后放入堆缩小后数组中空出的位置
①根据堆的性质,根结点的值最大,交换根结点和最后一个元素的位置
②交换后,数组的最后一个位置即是最大的元素,将堆的大小减小1
③因为有了一次交换,N-1的堆性质被打乱了,使用sink,维持堆的性质
④保持下去,直至所有的元素排完,即堆的大小为0
3.代码实现:
注意的是:因为这里假设堆的索引是1..N,而作为堆的载体数字的索引是0..N-1,因此,在比较大小和交换操作的时候,需要将索引-1

package com.cx.sort; public class Heapsort { public static void sort(Comparable[] pq) { int N=pq.length; //第一步,将数组pq构造为堆 //对有子结点的位置使用sink()操作,即1..N/2,自下而上 for(int k=N/2;k>=1;k--) sink(pq,k,N); //第二步,取最大值进行排序 //交换最大值与堆的最后一个元素,并维持堆 while(N>1) { exch(pq, 1, N--); sink(pq, 1, N); } } //将对象下沉 private static void sink(Comparable[] pq,int k,int n) { while(2*k<=n) { int j=2*k; //比较左右两个子结点 if(j<n && less(pq, j, j+1)) j++; //比较父结点和子结点 if(less(pq, j, k)) return; exch(pq, j, k); k=j; } } //堆做的定义是1..N,这里实际比较和交换时,需要将索引-1,,保证是0..N-1 private static boolean less(Comparable[] pq,int i,int j) { return pq[i-1].compareTo(pq[j-1])<0; } private static void exch(Comparable[] pq,int i,int j) { Comparable temp=pq[i-1]; pq[i-1]=pq[j-1]; pq[j-1]=temp; } public static void show(Comparable[] a) { for(int i=0;i<a.length;i++) { System.out.print(a[i]+" "); } System.out.println(); } public static void main(String[] args) { String a[]= {"s","o","r","t","e","x","a","m","p","l","e"}; show(a); sort(a); show(a); } }
4.说明:
(1)构造堆不超过2N比较和交换,而堆排序不超过2NlgN比较和交换
(2)堆排序不使用额外的空间,并且有NlgN的性能保障
(3)它是目前介绍的排序算法中唯一一个In-place sorting algorithm with NlgN worst-case
mergesort:需要额外的空间,来存放辅助数组
quicksort:最坏情况下,需要平方次时间
5.缺点:为什么堆排序在实际应用得不多?
(1)内循环比快速排序长。用到了两次比较(子结点之间,以子结点和父结点之间),需要2lgN
(2)没有充分利用缓存
(3)不稳定。因为有长距离的移动。
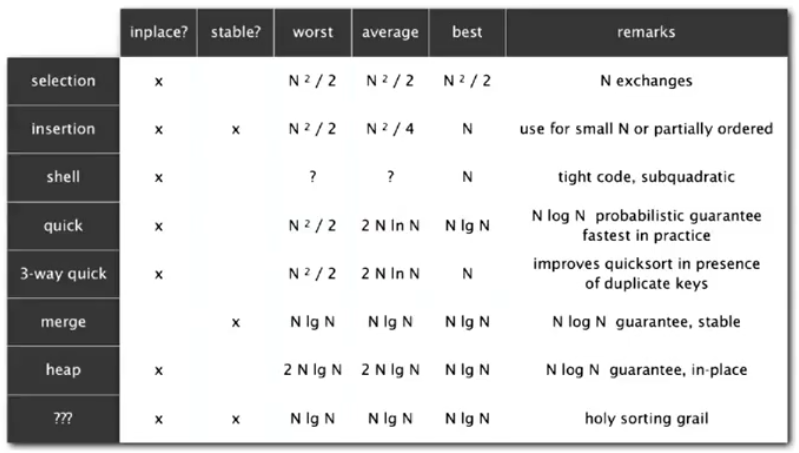
八.几种经典排序算法的比较。