Given two words (start and end), and a dictionary, find the length of shortest transformation sequence from start to end, such that:
- Only one letter can be changed at a time
- Each intermediate word must exist in the dictionary
For example,
Given:
start = "hit"
end = "cog"
dict = ["hot","dot","dog","lot","log"]
As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
Note:
- Return 0 if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic character
看了题解才发现要用BFS,题目中对应的深度优先搜索树如下:
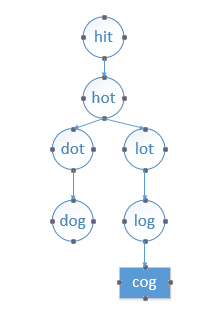
在维护队列的过程中,队列的变化如下:
[hit #] (distance=1) [# hot] [hot #] (distance=2) [# dot lot] [dot lot #] (distance=3) [lot # dog] [# dog log] [dog log #] (distance=4) 通过dog找到cog,返回distance+1=5
所以可以维护一个队列,初始化变量distance=1,先把start入队;每次从队列里面取出一个单词temp,看离temp只有一步的单词,如果有和end一样的,此时就找到了,返回distance就可以了,如果和end不一样但是出现在词典里面就推进队列,并把词典中相应的单词删除。树的每一层构建好以后,往队列里面存入一个“#”。怎么做到这一点呢?首先在start后面放一个"#",因为第一层只有一个单词,然后每次"#"出队的时候表示上一层遍历结束,这一层入队也结束,所以如果此时队列非空,就往队列中推进一个"#",对应distance就要加1,表示下一层生成完毕。最后直到队列为空,表示没找到end,返回0;或者找到end,返回distance+1。
代码如下:
class Solution { public: int ladderLength(string start, string end, unordered_set<string> &dict) { if(start == end) return 0; queue<string> q; q.push(start); q.push("#"); int distance = 1; int strLen = start.size(); dict.erase(start); while(!q.empty()){ string temp = q.front(); q.pop(); if(temp == "#") { if(!q.empty()){ distance++; q.push("#"); continue; } else return 0; } for(int i = 0;i < strLen;i++){ string t = temp; char m = t[i]; for(char c = 'a'; c <= 'z';c++){ if(c != m){ t[i] = c; if(t == end) return distance+1; else if(dict.find(t) != dict.end()){ q.push(t); dict.erase(t); } } } } } } };