（10）回归损失

目标检测任务的损失函数由Classificition Loss和Bounding Box Regeression Loss两部分构成。近几年来Bounding Box Regression Loss Function的演进过程，其演进路线是Smooth L1 Loss IoU LossGIoU Loss  DIoU Loss  CIoU Loss。

Smooth L1 LOSS

faster rcnn里面就是使用的这个loss：

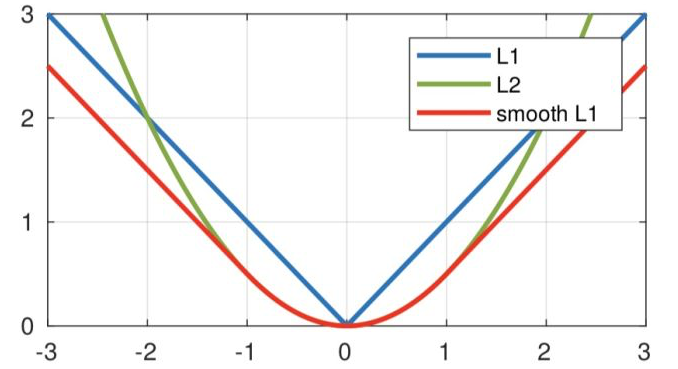
从损失函数对x的导数可知： L₁损失函数对x的导数为常数，在训练后期，x很小时，如果learning rate 不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。 L₂ 损失函数对x的导数在x值很大时，其导数也非常大，在训练初期不稳定。smooth_L1完美的避开了 前两个损失的缺点。而且从图像上也能看出smooth L1更加平滑。

缺点：

• 上面的三种Loss用于计算目标检测的Bounding Box Loss时，独立的求出4个点的Loss，然后进行相加得到最终的Bounding Box Loss，这种做法的假设是4个点是相互独立的，实际是有一定相关性的

• 实际评价框检测的指标是使用IOU，这两者是不等价的，多个检测框可能有相同大小的Loss，但IOU可能差异很大，为了解决这个问题就引入了IOU LOSS。

IOU Loss

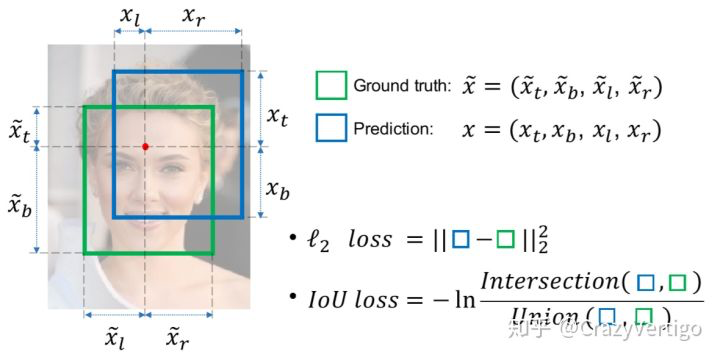
• 当预测框和目标框不相交时，IoU(A,B)=0时，不能反映A,B距离的远近，此时损失函数不可导，IoU Loss 无法优化两个框不相交的情况。
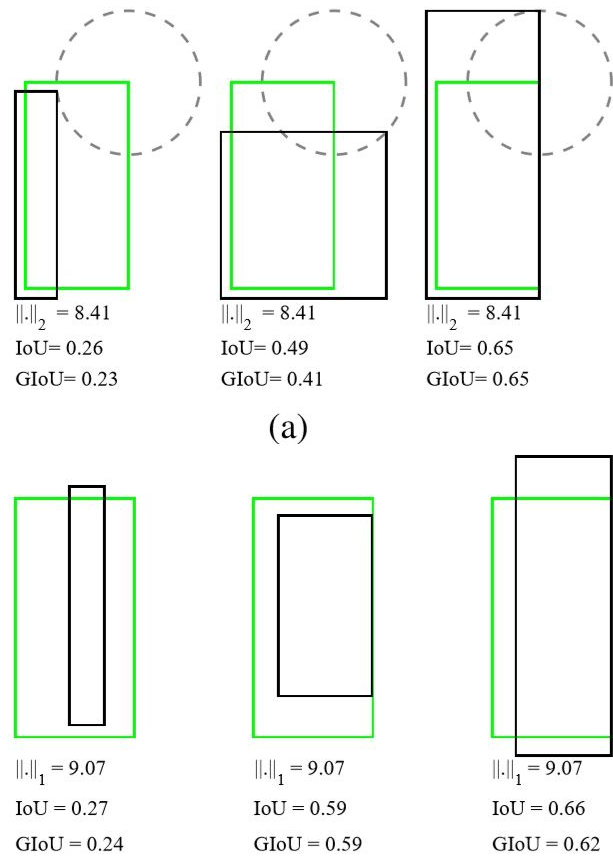
• 假设预测框和目标框的大小都确定，只要两个框的相交值是确定的，其IoU值是相同时，IoU值不能反映两个框是如何相交的。

 

三种不同相对位置的框拥有相同的IoU=0.33值，但是拥有不同的GIoU=0.33，0.24，-0.1。当框的对齐方向更好一些时GIoU的值会更高一些。

 GIOU Loss

GIoU考虑到，当检测框和真实框没有出现重叠的时候IoU的loss都是一样的，因此GIoU就加入了C检测框（C检测框是包含了检测框和真实框的最小矩形框），这样就可以解决检测框和真实框没有重叠的问题。但是当检测框和真实框之间出现包含的现象的时候GIoU就和IoU loss是同样的效果了。

 其中：C代表包围A、B的最小体积（或面积）。

性质：

1) 当IoU值为1时，GIoU 为 1，即|A U B| = |A ∩ B|；

2) Iou为0时，GIoU<=0;

3) -1<= GIoU <=1;

4) GIou <= IoU;

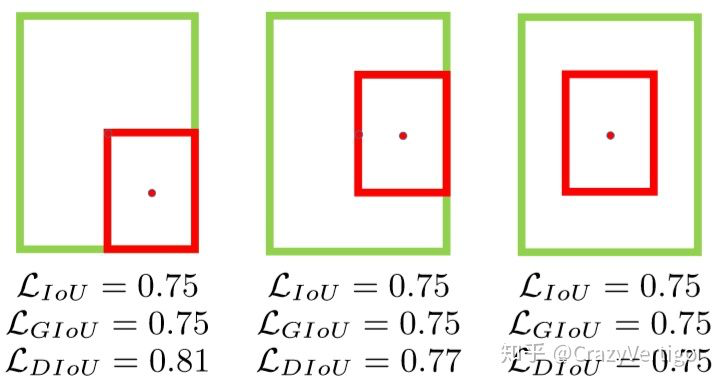
 当目标框完全包裹预测框的时候，IoU和GIoU的值都一样，此时GIoU退化为IoU, 无法区分其相对位置关系；此时作者提出的DIoU因为加入了中心点归一化距离，所以可以更好地优化此类问题。

DIOU Loss

b和 代表预测框的中心点和gt框的中心点。  代表的是欧式距离，c代表包含这两个框的最小矩形的对角线长度。这样的话，对于包含这种情况，中心点的距离也成为了一个评判标准，也能有一个优化的方向。

 

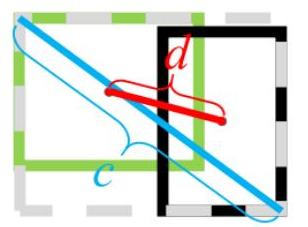
 性质：

• 尺度不变性
• 当两个框完全重合时，  ,当2个框不相交时
• DIoU Loss可以直接优化2个框直接的距离，比GIoU Loss收敛速度更快
• 对于目标框包裹预测框的这种情况，DIoU Loss可以收敛的很快，而GIoU Loss此时退化为IoU Loss收敛速度较慢

CIOU Loss

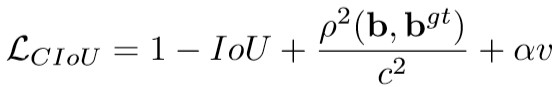
 CIoU就是在DIoU的基础上增加了检测框尺度的loss，增加了长和宽的loss，这样预测框就会更加的符合真实框。

上述损失函数中，CIoU比DIoU多出了α和v这两个参数。其中α是用于平衡比例的参数。v用来衡量anchor框和目标框之间的比例一致性。 从的定义式来看，损失函数会更加倾向于往重叠区域增多的方向优化，尤其是IoU为0的情况，这满足我们的要求。同时，在进行nms阶段，一般的评判标准是IOU，这个地方作者推荐替换为DIOU，这样考虑了中心点距离这一个信息，效果又有一定的提升。