堆
1 数组对象
2 可以视为一棵完全二叉树
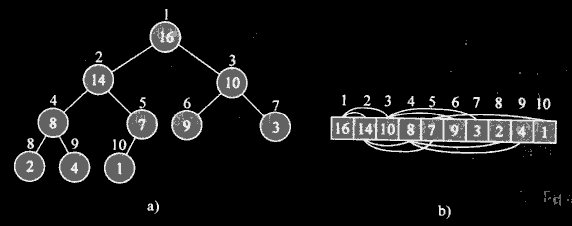
3 一个堆可以被看作一棵二叉树和一个数组,如下图所示:
4 下标计算(通常使用内联函数或者宏来定义下标操作):
- 已知某个结点的下标为i
- 其父节点下标:i/2向下取整
- 左孩子下标:2i
- 右孩子下标:2i+1
5 最大堆:除根节点以外的每个节点i,有A[PARENT(i)] >= A[i]
最小堆:除根节点意外的每个节点i,有A[PARENT(i)] <= A[i]
堆排序
步骤:
- 建大顶堆
- 去堆顶元素与当前堆的最后一个元素进行互换。
- 该堆顶元素已达最终位置,排除出堆
- 对剩下的堆进行最大堆调整
- 重复2到4步
排序过程
1 建堆过程
1) 从第一个非叶子节点开始,对value为8的节点进行调整,无需调整。
2) 对value值为9的节点进行调整。
3) 对value为2的节点调整
4) 对value为3的节点进行调整
5) 对value为7的节点进行调整
建堆完成
2 堆顶元素与当前堆的最后一个元素进行互换。
3 该堆顶元素已达最终位置,排除出堆
4 对剩下的堆进行调整
递归进行堆首和堆尾互换以及调整堆的步骤,结果即为排好序的堆。
代码实现
// heapsort.h
class HeapSort:public BaseSort {
public:
HeapSort(int Array[], int len) : BaseSort() {
this->Array = Array;
this->len = len;
}
void sort();
private:
/* 建堆 */
void buildMaxHeap();
/* 调整堆,以保持最大堆性质 */
void maxHeapIfy( int i , int curlen);
/* 堆排序 */
void heapSort();
/* 返回父节点下标 */
int Parent(int i) {
if ( i % 2 == 0 )
return i/2;
else
return i/2 + 1;
};
/* 返回左孩子节点下标 */
int Left(int i) { return 2 * i + 1; };
/* 返回右孩子节点下标 */
int Right(int i) { return 2 * i + 2; };
private:
int* Array;
int len;
};
相关成员函数实现
// heapsort.cpp
#include "heapsort.h"
void HeapSort::sort() {
heapSort();
}
void HeapSort::heapSort() {
buildMaxHeap();
int i = this->len;
int tmp;
while( i > 0 ) {
tmp = this->Array[0];
this->Array[0] = this->Array[i-1];
this->Array[i-1] = tmp;
i--;
maxHeapIfy(0, i);
}
}
void HeapSort::maxHeapIfy( int i, int curlen ) {
int left, right, largest;
int tmp;
left = Left(i);
right = Right(i);
if ( left < curlen-1
&& Array[left] > Array[i])
largest = left;
else
largest = i;
if ( right < curlen-1
&& Array[right] > Array[largest])
largest = right;
if ( largest != i ) {
tmp = Array[i];
Array[i] = Array[largest];
Array[largest] = tmp;
maxHeapIfy(largest, curlen);
}
}
void HeapSort::buildMaxHeap() {
int i;
for ( i = (len-1)/2 ; i >= 0; i-- ) {
maxHeapIfy(i, len);
if (DEBUG) {
printArray(this->Array, this->len, "midResult");
}
}
}测试代码: /* --------- HeapSort -------- */
int b[10] = {7,3,2,9,8,5,1,10,4,6};
HeapSort* heapsort = new HeapSort(b, len);
heapsort->sort();
printArray(b, len, "HeapSort ");
参考资料:
《算法导论 2rd》
http://www.cnblogs.com/Anker/archive/2013/01/23/2873422.html 《算法导论》读书笔记之第6章 堆排序
![clipboard[1] clipboard[1]](https://images0.cnblogs.com/blog/526303/201405/271055118536226.png)
![clipboard[2] clipboard[2]](https://images0.cnblogs.com/blog/526303/201405/271055137911369.png)
![clipboard[3] clipboard[3]](https://images0.cnblogs.com/blog/526303/201405/271055158696767.png)
![clipboard[4] clipboard[4]](https://images0.cnblogs.com/blog/526303/201405/271055168388837.png)
![clipboard[5] clipboard[5]](https://images0.cnblogs.com/blog/526303/201405/271055177288464.png)
![clipboard[6] clipboard[6]](https://images0.cnblogs.com/blog/526303/201405/271055186668779.png)
![clipboard[7] clipboard[7]](https://images0.cnblogs.com/blog/526303/201405/271055194633136.png)
![clipboard[8] clipboard[8]](https://images0.cnblogs.com/blog/526303/201405/271055204785491.png)
![clipboard[9] clipboard[9]](https://images0.cnblogs.com/blog/526303/201405/271055215418534.png)
![clipboard[10] clipboard[10]](https://images0.cnblogs.com/blog/526303/201405/271055223382891.png)
![clipboard[11] clipboard[11]](https://images0.cnblogs.com/blog/526303/201405/271055232757503.png)
![clipboard[12] clipboard[12]](https://images0.cnblogs.com/blog/526303/201405/271055242752332.png)