poj2125 最小点权覆盖集

 题意:有一张图，对于每个点，有出边和入边，现在目的是删除改图的所有边，对于每个点，删除出边的花费Wi-，删除入边的花费Wi+，现在的目的求删去所有边后的花费最小。

建图方法:对于每个点i，拆点为i，i+n，对于入边，从i+n想汇点T连边，值为入边花费；对于出边，从S向i连边，权值为出边花费。m组相连的边（x,y），从x向y+n连边， 费用INF。求出最小割。

然后是计算删除的是哪些点。对于完成最小割后的图，从源点S进行dfs，如果能够访问到，标记。对于不能访问到的点，i<=n时，这个点的出边是属于割集的，即所求点，且为‘-’；如果i>n，表示该点为需要删除的边的点，为'+'；

最小割后的图片

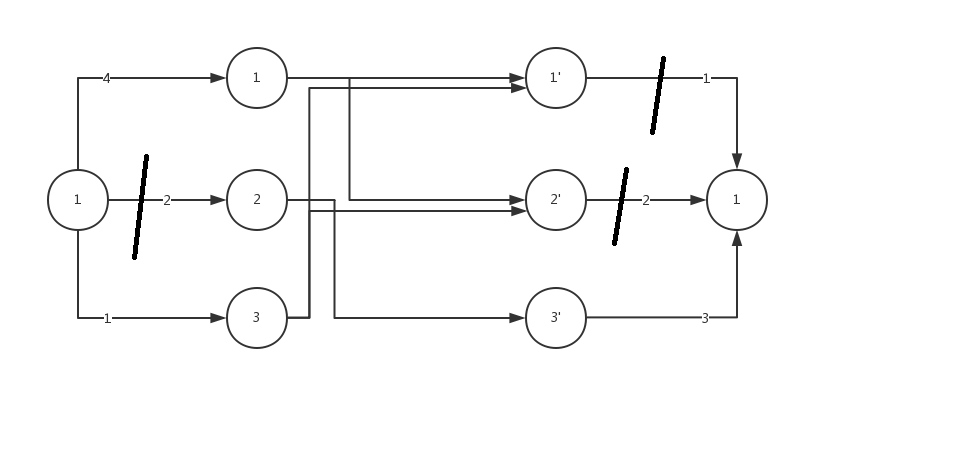(ps:S,T写错了。。。)

根据图很明显的可以看出哪些边时需要删除，并且是哪些点的边。

#include<stdio.h>
#include<string.h>
#include<queue>
#define INF 99999999
using namespace std;
const int maxn = 120*2;
const int maxm = 5010;
struct node
{
    int to;
    int v;
    int flag;
    int next;
}edge[(maxn+maxm)*2];
struct ans_point
{
    int x;
    int flag;
}ans_p[maxn];
int index,pre[maxn],vis[maxn],S,T;
int in[maxn],out[maxn];
void add(int x,int y,int z)
{
    edge[index].to=y;
    edge[index].v=z;
    edge[index].flag=index+1;
    edge[index].next=pre[x];
    pre[x]=index++;
    edge[index].to=x;
    edge[index].v=0;
    edge[index].flag=index-1;
    edge[index].next=pre[y];
    pre[y]=index++;
}
int dfs(int u,int low)
{
    int i,used=0;
    if(u==T)
        return low;
    for(i=pre[u];i!=-1&&used<low;i=edge[i].next)
    {
        if(edge[i].v&&vis[edge[i].to]==vis[u]+1)
        {
            int a=dfs(edge[i].to,min(low-used,edge[i].v));
            edge[i].v-=a;
            edge[edge[i].flag].v+=a;
            used+=a;
        }
    }
    if(!used)
        vis[u]=-1;
    return used;
}
bool BFS()
{
    int i;
    queue<int>q;
    memset(vis,-1,sizeof(vis));
    vis[0]=1;
    q.push(0);
    while(!q.empty())
    {
        int t=q.front();
        q.pop();
        for(i=pre[t];i!=-1;i=edge[i].next)
        {
            if(edge[i].v&&vis[edge[i].to]<0)
            {
                vis[edge[i].to]=vis[t]+1;
                q.push(edge[i].to);
            }
        }
    }
    if(vis[T]>0)
        return true;
    return false;
}
void cnt_dfs(int u)
{
    int i;
    vis[u]=1;
    for(i=pre[u];i!=-1;i=edge[i].next)
    {
        if(edge[i].v>0&&!vis[edge[i].to])
            cnt_dfs(edge[i].to);
    }
}
int main()
{
    int n,m,i,j;
    while(~scanf("%d%d",&n,&m))
    {
        index=1;
        memset(pre,-1,sizeof(pre));
        S=0,T=2*n+1;
        for(i=1;i<=n;i++)
        {
            scanf("%d",&in[i]);
            add(i+n,T,in[i]);
        }
        for(i=1;i<=n;i++)
        {
            scanf("%d",&out[i]);
            add(S,i,out[i]);
        }
        while(m--)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            add(x,y+n,INF);
        }
        int ans=0;
        while(BFS())
        {
            int a=dfs(0,INF);
            if(!a)break;
            ans+=a;
        }
        printf("%d
",ans);
        memset(vis,0,sizeof(vis));
        cnt_dfs(0);
        int cnt=0;
        for(i=1;i<=n*2;i++)
        {
            if(i>n)
            {
                if(vis[i])
                {
                    ans_p[cnt].x=i;
                    ans_p[cnt++].flag=1;
                }
            }
            else
            {
                if(!vis[i])
                {
                    ans_p[cnt].x=i;
                    ans_p[cnt++].flag=0;
                }
            }
        }
        printf("%d
",cnt);
        for(i=0;i<cnt;i++)
        {
            if(ans_p[i].x>n)
                    printf("%d ",ans_p[i].x-n);
            else printf("%d ",ans_p[i].x);
            if(ans_p[i].flag==0)
                printf("-
");
            else printf("+
");
        }
    }
}